لعنة الأبعاد
نشرت: 2015-07-08ما هي لعنة الأبعاد
تشير لعنة الأبعاد إلى الخصائص غير البديهية للبيانات التي يتم ملاحظتها عند العمل في مساحة عالية الأبعاد * ، وتتعلق على وجه التحديد بقابلية الاستخدام وتفسير المسافات والأحجام. هذا هو أحد موضوعاتي المفضلة في التعلم الآلي والإحصاء نظرًا لأنه يحتوي على تطبيقات واسعة (ليست خاصة بأي طريقة للتعلم الآلي) ، وهو غير بديهي للغاية وبالتالي فهو مثير للإعجاب ، وله تطبيق عميق لأي من تقنيات التحليلات ، و له اسم مخيف "رائع" مثل لعنة مصرية!
لفهم سريع ، ضع في اعتبارك هذا المثال: لنفترض أنك أسقطت عملة معدنية على خط 100 متر. كيف وجدته؟ بسيط ، ما عليك سوى السير على الخط والبحث. لكن ماذا لو كانت 100 × 100 متر مربع. حقل؟ لقد أصبح الأمر صعبًا بالفعل ، في محاولة البحث (تقريبًا) عن ملعب كرة قدم لعملة واحدة. ولكن ماذا لو كانت مساحة 100 × 100 × 100 متر مكعب ؟! كما تعلم ، يبلغ ارتفاع ملعب كرة القدم الآن ثلاثين طابقًا. حظا سعيدا في العثور على عملة هناك! هذا ، في جوهره ، هو "لعنة الأبعاد".
تستخدم العديد من طرق ML قياس المسافة
تعتمد معظم طرق التجزئة والتجميع على حساب المسافات بين الملاحظات. إن تجزئة k-Means المعروفة تعين نقاطًا لأقرب مركز. تتطلب مجموعات DBSCAN والتسلسل الهرمي أيضًا مقاييس المسافة. تستفيد خوارزميات الكشف عن العوامل الخارجية القائمة على التوزيع والكثافة أيضًا من المسافة بالنسبة إلى المسافات الأخرى لتحديد القيم المتطرفة.
تستخدم حلول التصنيف الخاضعة للإشراف مثل طريقة k-Nearest Neighbours أيضًا المسافة بين الملاحظات لتعيين فئة إلى ملاحظة غير معروفة. تتضمن طريقة Support Vector Machine تحويل الملاحظات حول نواة محددة بناءً على المسافة بين الملاحظة والنواة.
يشتمل الشكل الشائع لأنظمة التوصية على تشابه قائم على المسافة بين متجهات سمات المستخدم والعنصر. حتى عند استخدام أشكال أخرى من المسافات ، يلعب عدد الأبعاد دورًا في التصميم التحليلي.
يعد مقياس المسافة الإقليدية أحد أكثر مقاييس المسافة شيوعًا ، وهو ببساطة مسافة خطية بين نقطتين في مساحة مفرطة متعددة الأبعاد. يمكن حساب المسافة الإقليدية للنقطة i والنقطة j في مساحة الأبعاد n على النحو التالي:
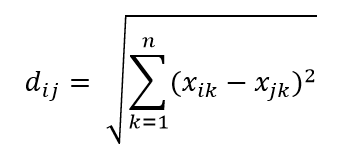
المسافة تلعب الفوضى في الأبعاد العالية
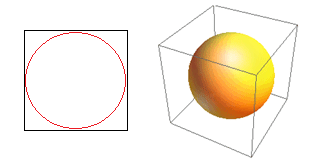
ضع في اعتبارك عملية بسيطة لأخذ عينات البيانات. لنفترض أن الصندوق الخارجي الأسود في الشكل 1 عبارة عن كون بيانات مع توزيع منتظم لنقاط البيانات عبر الحجم الكامل ، وأننا نريد أخذ عينة من 1٪ من الملاحظات كما هو محاط بمربع داخلي أحمر. الصندوق الأسود عبارة عن مكعب فائق في مساحة متعددة الأبعاد حيث يمثل كل جانب نطاقًا من القيمة في هذا البعد. لمثال بسيط ثلاثي الأبعاد في الشكل 1 ، قد يكون لدينا النطاق التالي:
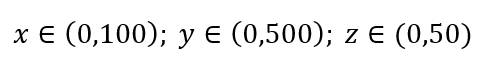
الشكل 1: أخذ العينات
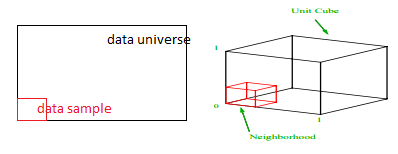
ما هي النسبة من كل نطاق التي يجب أخذ عينات منها للحصول على عينة 1٪؟ بالنسبة للأبعاد ثنائية الأبعاد ، سيحقق 10٪ من النطاق أخذ عينات إجمالي بنسبة 1٪ ، لذلك قد نختار x∈ (0،10) و y∈ (0،50) ونتوقع التقاط 1٪ من جميع الملاحظات. وذلك لأن 10٪ 2 = 1٪. هل تتوقع أن تكون هذه النسبة أعلى أم أقل للأبعاد الثلاثة؟
على الرغم من أن بحثنا الآن في اتجاه إضافي ، إلا أن النسبة تزداد بالفعل إلى 21.5٪. وليس الزيادات فقط ، وإنما لبُعد إضافي واحد فقط ، بل تتضاعف! ويمكنك أن ترى أنه يتعين علينا تغطية ما يقرب من خُمس كل بُعد فقط للحصول على واحد على المائة من الإجمالي! في 10 أبعاد ، تبلغ هذه النسبة 63٪ وفي 100 بُعد - وهو عدد غير مألوف من الأبعاد في أي تعلم آلي حقيقي - يتعين على المرء أن يأخذ عينة من 95٪ من النطاق على طول كل بُعد لأخذ عينة من 1٪ من الملاحظات! تحدث هذه النتيجة المذهلة لأنه في الأبعاد العالية ، يصبح انتشار نقاط البيانات أكبر حتى لو كانت منتشرة بشكل موحد.

هذا له نتيجة من حيث تصميم التجربة وأخذ العينات. تصبح العملية مكلفة للغاية من الناحية الحسابية ، حتى لدرجة أن أخذ العينات يقترب من السكان بشكل مقارب على الرغم من بقاء حجم العينة أصغر بكثير من السكان.
لنتأمل في نتيجة أخرى ضخمة للأبعاد العالية. تقيس العديد من الخوارزميات المسافة بين نقطتي بيانات لتحديد نوع من القرب (DBSCAN ، Kernels ، k-Nearest Neighbor) في إشارة إلى بعض عتبة المسافة المحددة مسبقًا. في بعدين ، يمكننا أن نتخيل أن نقطتين قريبتين إذا كانت إحداهما تقع ضمن نصف قطر معين من الأخرى. ضع في اعتبارك الصورة اليسرى في الشكل 2. ما هو نصيب النقاط المتباعدة بشكل موحد داخل المربع الأسود الذي يقع داخل الدائرة الحمراء؟ ذلك عن
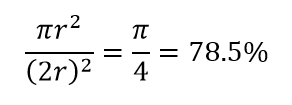
الشكل 2: القرب
لذلك إذا قمت بتركيب أكبر دائرة ممكنة داخل المربع ، فإنك تغطي 78٪ من المربع. ومع ذلك ، فإن أكبر مجال ممكن داخل المكعب يغطي فقط
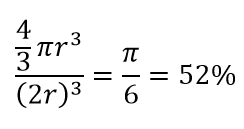
من الحجم. هذا الحجم ينخفض بشكل كبير إلى 0.24٪ لـ 10 أبعاد فقط! ما يعنيه ذلك أساسًا أنه في العالم عالي الأبعاد ، تكون كل نقطة بيانات مفردة في الزوايا ولا يوجد شيء يمثل مركز الحجم حقًا ، أو بعبارة أخرى ، يتقلص حجم المركز إلى لا شيء لأنه لا يوجد (تقريبًا) مركز! هذا له عواقب هائلة من خوارزميات التجميع القائمة على المسافة. تبدأ جميع المسافات في أن تبدو متشابهة وأي مسافة أكثر أو أقل من الأخرى هي تقلب عشوائي في البيانات بدلاً من أي مقياس للاختلاف!
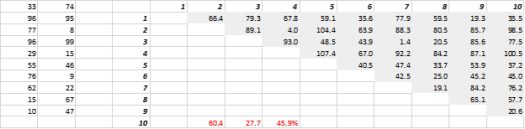
يوضح الشكل 3 بيانات ثنائية الأبعاد تم إنشاؤها عشوائيًا وما يقابلها من مسافات شاملة. معامل التباين في المسافة ، محسوبًا على أنه الانحراف المعياري مقسومًا على المتوسط ، هو 45.9٪. العدد المقابل لبيانات 5-D التي تم إنشاؤها بشكل مشابه هو 26.5٪ و 10-D هو 19.1٪. من المسلم به أن هذه عينة واحدة ، لكن الاتجاه يدعم الاستنتاج القائل بأن كل مسافة في الأبعاد العالية هي نفسها تقريبًا ، ولا يوجد شيء قريب أو بعيد!
الشكل 3: المسافة العنقودية
يؤثر البعد العالي على أشياء أخرى أيضًا
بصرف النظر عن المسافات والأحجام ، فإن عدد الأبعاد يخلق مشاكل عملية أخرى. غالبًا ما تتصاعد متطلبات وقت تشغيل الحل وذاكرة النظام بشكل غير خطي مع زيادة عدد الأبعاد. نظرًا للزيادة الهائلة في الحلول الممكنة ، لا يمكن للعديد من طرق التحسين الوصول إلى Optima العالمي ويجب أن تتعامل مع Optima المحلي. علاوة على ذلك ، بدلاً من الحل المغلق ، يجب أن يستخدم التحسين الخوارزميات القائمة على البحث مثل النسب المتدرج ، والخوارزمية الجينية ، والتلدين المحاكي. المزيد من الأبعاد تقدم إمكانية الارتباط ويمكن أن يصبح تقدير المعلمات صعبًا في مناهج الانحدار.
التعامل مع الأبعاد العالية
ستكون هذه مشاركة مدونة منفصلة في حد ذاتها ، لكن تحليل الارتباط والتجميع وقيمة المعلومات وعامل تضخم التباين وتحليل المكون الرئيسي هي بعض الطرق التي يمكن من خلالها تقليل عدد الأبعاد.
* يُطلق على عدد المتغيرات أو الملاحظات أو الميزات التي تتكون منها نقطة البيانات اسم بُعد البيانات. على سبيل المثال ، يمكن تمثيل أي نقطة في الفضاء باستخدام 3 إحداثيات للطول والعرض والارتفاع ، ولها 3 أبعاد
