تقدير الكثافة باستخدام الرسوم البيانية

تصف وظائف الكثافة الاحتمالية (PDFs) احتمالية ملاحظة بعض المتغيرات العشوائية المستمرة في منطقة معينة من الفضاء. بالنسبة لمتغير عشوائي X أحادي البعد ، تذكر أن PDF f (x) يتبع الخصائص التي

احتمال أن يأخذ هذا المتغير القيم بين

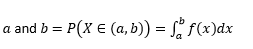
احتمال أن يأخذ هذا المتغير قيمًا تساوي تمامًا

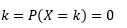
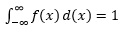
يعد تقدير ملف PDF هذا من عينة الملاحظات مشكلة شائعة في التعلم الآلي. يكون هذا مفيدًا في العديد من خوارزميات الكشف الخارجية حيث نسعى لتقدير التوزيع "الحقيقي" بناءً على ملاحظات العينة ثم نصنف بعض الملاحظات الحالية أو الجديدة على أنها خارجية أو لا. على سبيل المثال ، قد تقوم شركة التأمين على السيارات المهتمة بالقبض على الاحتيال بفحص طلب مبلغ المطالبة لكل نوع من أنواع أعمال الجسم ، على سبيل المثال ، استبدال المصد ، وتحديد أي مبلغ مرتفع للغاية على الاحتيال المحتمل. كمثال آخر ، قد يقوم أخصائي نفس الأطفال بفحص الوقت المستغرق لإكمال مهمة معينة عبر أطفال مختلفين ويضع علامة على هؤلاء الأطفال الذين يستغرقون وقتًا طويلاً جدًا أو قصيرًا جدًا لإجراء تحقيق محتمل.

في منشور المدونة هذا ، نناقش كيف يمكننا تعلم ملف PDF من عينة الملاحظات ، حتى نتمكن من حساب الاحتمالية لكل ملاحظة وتحديد ما إذا كانت شائعة أو نادرة الحدوث.

تقدير الكثافة باستخدام الرسم البياني

أولاً نقوم بإنشاء بعض البيانات العشوائية للتوضيح.

set.seed(123)
data <- c(rnorm(200, 10, 20), rnorm(200, 60, 30), runif(200, 120, 180)) # 600 points

بعد ذلك ، نتخيلها لفهمنا ، باستخدام الرسم البياني ، كما في الشكل 1.

# Plot 1
hist(data, breaks=50, freq=F, main="Univariate Distribution", xlab="Data Value")
# Plot 2
hist(data, breaks=20, freq=F, main="", xlab="20 Data Bins", col='red', border='red')
par(new=T)
hist(data, breaks=100, freq=F, main="Univariate Distribution", xlab=NULL, xaxt='n', yaxt='n')

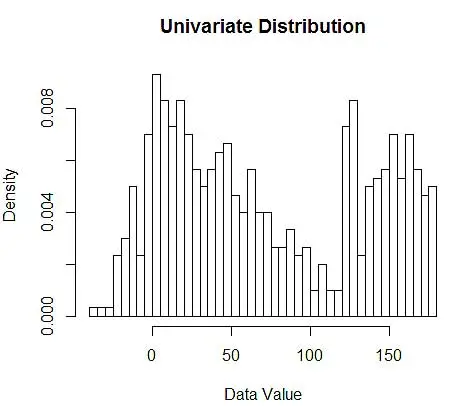
في حين أن الرسوم البيانية هي مخططات لتصور البيانات ، يمكنك أيضًا أن ترى أنها أول تقدير لنا للكثافة. وبشكل أكثر تحديدًا ، يمكننا تقدير الكثافة عن طريق تقسيم البيانات إلى سلال وافتراض أن الكثافة ثابتة ضمن نطاق الحاوية هذا ولها قيمة مساوية لعدد الملاحظات التي تقع في تلك الحاوية كنسبة من إجمالي عدد الملاحظات

ومن ثم ، فإن PDF المقدّر هو

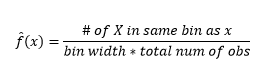
وأنت تدرك أنك قمت بافتراض حول عرض الصندوق الذي سيؤثر على تقدير الكثافة. ومن ثم فإن عرض الصندوق هو معلمة لنموذج تقدير الكثافة باستخدام الرسم البياني . ومع ذلك ، فإن الحقيقة التي تم التغاضي عنها هي أننا نعمل أيضًا مع معلمة أخرى - وهي موضع البداية للحاوية الأولى . يمكنك أن ترى كيف يمكن أن يؤثر ذلك على تقديرات الكثافة لجميع الصناديق. لمعرفة تأثير عرض الحاوية ، يقوم الشكل 2 بتراكب تقديرات الكثافة برسوم بيانية 20 حاوية و 100 حاوية. انظر إلى المنطقة المحاطة بدائرة ، حيث تعطي الصناديق الأقل / الخشنة تقديرًا للكثافة المسطحة ، بينما تعطي العديد من الصناديق / الدقيقة تقديرًا متباينًا للكثافة. بالنسبة للنقطة الصفراء ، تتراوح تقديرات الكثافة من 0.004 إلى 0.008 من نموذجين مختلفين.

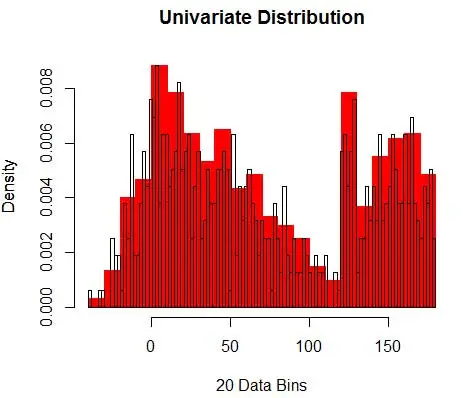
وبالتالي ، فإن اختيار المعلمات الصحيحة أمر بالغ الأهمية للحصول على تقدير الكثافة الصحيح. سنصل إلى ذلك ، لكن لاحظ أن هناك أيضًا مشاكل أخرى في الرسوم البيانية. تقديرات الكثافة باستخدام الرسوم البيانية متقطعة ومتقطعة تمامًا . تكون الكثافة مسطحة بالنسبة للحاوية ثم تتغير فجأة بشكل جذري لنقطة غير متناهية الصغر خارج السلة. هذا يجعل نتيجة التقدير الخاطئ أسوأ بالنسبة للمشاكل العملية.

أخيرًا ، لقد عملنا مع متغير أحادي البعد لسهولة التوضيح ، ولكن من الناحية العملية ، فإن معظم المشكلات متعددة الأبعاد. نظرًا لأن عدد الصناديق ينمو بشكل كبير مع عدد الأبعاد ، فإن عدد الملاحظات المطلوبة لتقدير الكثافة ينمو أيضًا . في الواقع ، من المعقول أنه على الرغم من وجود ملايين الملاحظات ، تظل العديد من الصناديق فارغة أو تحتوي على ملاحظات مكونة من رقم واحد. مع وجود 50 حاوية فقط في 3 أبعاد فقط ، لدينا 503 = 125000 خلية يجب ملؤها. يأتي ذلك بمعدل 8 ملاحظات لكل خلية ، بافتراض التوزيع المنتظم ، مليون من بيانات التدريب على الملاحظة.

كيفية تحديد المعلمات الصحيحة؟

بالنسبة إلى bin-width n ، فإن عدد الملاحظات N لـ bin J هو نسبة الملاحظات

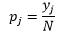
وتقدير الكثافة

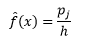
تثبت النظرية الإحصائية أنه في حين أن f (x) هي القيمة المتوقعة للكثافة في السلة ، فإن تباين الكثافة هو

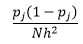
بينما يمكننا الحصول على تقدير أفضل للكثافة عن طريق تقليل عرض الحاوية n ، فإننا نزيد من تباين التقدير ، حيث يمكننا أن نشعر بشكل بديهي حول عرض الصندوق الدقيق جدًا. يمكننا استخدام تقنية التحقق المتقاطع لمرة واحدة لتقدير المجموعة المثلى من المعلمات. يمكننا تقدير الكثافة باستخدام جميع الملاحظات باستثناء واحدة ، ثم حساب كثافة تلك الملاحظة المتروكة وقياس الخطأ في التقدير. يعطي حل هذه الرسوم البيانية للرسوم البيانية حلاً مغلقًا لوظيفة الخسارة لعرض حاوية معين.

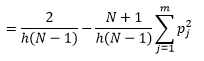
حيث م هو عدد الصناديق. التفاصيل الفنية المذكورة أعلاه موجودة في هذه المحاضرة [pdf]. يمكننا رسم وظيفة الخسارة هذه لعدد مختلف من الصناديق (الشكل 3)

getLoss <- function(n.break) {
N <- 600
res <- hist(data, breaks=n.break, freq=F)
bin <- as.numeric(res$breaks)
h <- bin[2]-bin[1]
p <- res$density
p <- p * h
return ( 2/(h*(N-1)) - ( (N+1)/(h*(N-1))*sum(p*p) ) )
}
loss.func <- data.frame(n=1:600)
loss.func$J <- sapply(loss.func$n, function(x) getLoss(x))
# Plot 3
plot(loss.func$n, loss.func$J, col='red', type='l')
opt.break <- max(loss.func[loss.func$J == min(loss.func$J), 'n'])
print(opt.break)
# Plot 4
hist(data, breaks=opt.break, freq=F, main="Univariate Distribution", xlab="15 Data Bins")

والحصول على الرقم الأمثل كـ 15. في الواقع ، أي شيء من 8 إلى 15 جيد.

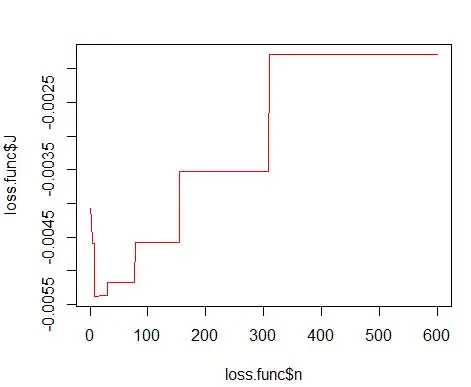
وبالتالي ، يوجد أدناه الشكل 4 تقدير الكثافة الذي يوازن قيم الكثافة بالإضافة إلى الدقة (مع مقايضة التباين التحيز الأمثل).

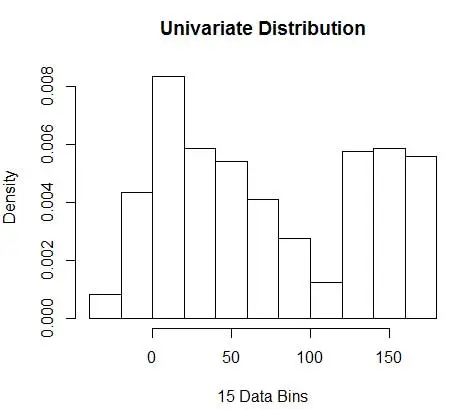
إذا كنت تشعر بعدم الارتياح قليلاً في هذه المرحلة فأنا معك. على الرغم من أن عدد الصناديق هو الأمثل رياضيًا ، إلا أنه يبدو تقديراً فظاً للغاية. ليس هناك شعور بديهي لماذا قمنا بأفضل عمل. وعدم نسيان الاهتمامات الأخرى المتعلقة بوضعية البداية والتقدير المتقطع ولعنة الأبعاد. لا ديال ، هناك طريقة أفضل. في المقالة التالية سوف نتحدث عن تقدير الكثافة باستخدام Kernels.