قياس المسافة في Hyperspace

قد يلاحظ أي شخص مطلع على التقنيات التحليلية الكثير من الخوارزميات التي تعتمد على المسافات بين نقاط البيانات لتطبيقها. عادةً ما يتم تمثيل كل ملاحظة ، أو مثيل بيانات ، على شكل متجه متعدد الأبعاد ، ويتطلب الإدخال إلى الخوارزمية مسافات بين كل زوج من هذه الملاحظات.

تعتمد طريقة حساب المسافة على نوع البيانات - رقمية أو فئوية أو مختلطة. تنطبق بعض الخوارزميات على فئة واحدة فقط من الملاحظات ، بينما يعمل البعض الآخر على أكثر من فئة. في هذا المنشور ، سنناقش مقاييس المسافة التي تعمل على البيانات الرقمية. ربما توجد طرق أكثر يمكن من خلالها قياس المسافة في المسافات الزائدة متعددة الأبعاد أكثر من تلك التي يمكن تغطيتها في منشور مدونة واحد ، ويمكن للمرء دائمًا ابتكار طرق أحدث ، لكننا ننظر في بعض مقاييس المسافة الشائعة ومزاياها النسبية.

لغرض بقية منشور المدونة ، فإننا نعني

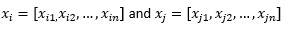
للإشارة إلى اثنين من الملاحظات أو ناقلات البيانات.

أولاً جهِّز البيانات ...

قبل أن نراجع مقاييس المسافة المختلفة ، نحتاج إلى إعداد البيانات:

التحول إلى ناقل رقمي

بالنسبة للملاحظة المختلطة ، التي تحتوي على أبعاد عددية وفئوية ، فإن الخطوة الأولى هي تحويل البعد الفئوي في الواقع إلى بعد (أبعاد) عددية. يمكن تحويل البعد الفئوي بثلاث قيم محتملة إلى بعدين أو ثلاثة أبعاد رقمية بقيم ثنائية. نظرًا لأن هذا المتغير الفئوي يأخذ بالضرورة واحدة من ثلاث قيم ، فسيكون أحد الأبعاد الرقمية الثلاثة مرتبطًا تمامًا مع اثنين آخرين. قد يكون هذا أو لا يكون على ما يرام اعتمادًا على التطبيق الخاص بك.

إذا كانت الملاحظة قاطعة تمامًا ، مثل سلسلة نصية (جمل متفاوتة الطول) أو تسلسل الجينوم (متواليات طول ثابت) ، فيمكن عندئذٍ تطبيق بعض مقاييس المسافة الخاصة مباشرةً دون تحويل البيانات إلى تنسيق رقمي. سنناقش هذه الخوارزميات في المنشور التالي.

تطبيع

اعتمادًا على حالة الاستخدام الخاصة بك ، قد ترغب في تسوية كل بُعد على نفس المقياس ، بحيث لا تؤثر المسافة على طول أي بُعد واحد بلا داع على المسافة الإجمالية بين الملاحظات. تمت مناقشة نفس الشيء في خوارزمية k-Means. هناك نوعان ممكنان من التطبيع:

يعمل تسوية النطاق (إعادة القياس) على تسوية البيانات لتكون في نطاق 0-1 ، عن طريق طرح الحد الأدنى للقيمة من كل بُعد ثم القسمة على نطاق القيم في هذا البعد.

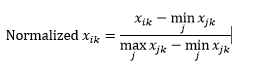
المشكلة الأولى في تسوية النطاق هي أن القيمة غير المرئية يمكن تطبيعها خارج النطاق 0-1. على الرغم من أن هذا لا يمثل مصدر قلق بشكل عام لمعظم مقاييس المسافة ، ولكن إذا لم تتمكن الخوارزمية من التعامل مع القيم السالبة ، فقد تكون هذه مشكلة. المشكلة الثانية هي أن هذا يعتمد بشكل كبير على القيم المتطرفة. إذا كانت إحدى الملاحظات ذات قيمة شديدة (عالية أو منخفضة) لبعد ما ، فسيتم تجميع القيمة العادية لهذا البعد للملاحظات الأخرى معًا وتفقد قوتها التمييزية.

يقوم التطبيع القياسي (مقياس z) بتطبيع البعد ليكون له متوسط ​​0 وانحراف معياري واحد ، عن طريق طرح المتوسط ​​من هذا البعد لكل ملاحظة ثم القسمة على الانحراف المعياري لقيمة هذا البعد عبر جميع الملاحظات.

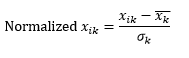
هذا بشكل عام يحافظ على البيانات في نطاق -5 إلى +5 تقريبًا ، ويتجنب تأثير القيمة القصوى.

لقد قمنا بمحاكاة قياس z لملاحظتين. محاكاة ، لأننا نحتاج حقًا إلى أكثر من ملاحظتين لحساب المتوسط ​​والانحراف المعياري لكل بُعد ، وقد افترضنا هذين الرقمين لكل بُعد هنا.

ثم احسب المسافة ...

المسافة الإقليدية - المعروفة أيضًا باسم "المسافة التي يطير بها الغراب" - هي أقصر مسافة في الفضاء الفائق متعدد الأبعاد بين نقطتين. أنت معتاد على هذا في المستوى ثنائي الأبعاد أو الفضاء ثلاثي الأبعاد (هذا خط) ، لكن المفهوم المماثل يمتد إلى أبعاد أعلى. يتم حساب المسافة الإقليدية بين المتجهات في الفضاء ذي الأبعاد n على شكل

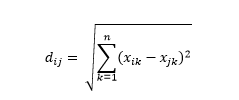
لأمثلة ناقلات البيانات المحولة ، هذا هو

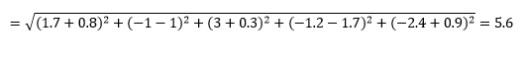
هذا هو المقياس الأكثر شيوعًا وغالبًا ما يكون مناسبًا جدًا لمعظم التطبيقات. البديل من هذا هو المسافة الإقليدية التربيعية ، والتي هي مجرد مجموع تربيع الفروق.

مسافة مانهاتن - التي سميت بسبب شبكة تشبه بنية شوارع مانهاتن في نيويورك بين الشرق والغرب والشمال والجنوب - هي المسافة بين نقطتين عند العبور بالتوازي مع المحاور.

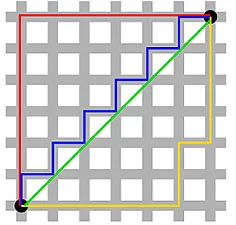
مسافة مانهاتن
المسافة الإقليدية

هذا محسوب كـ

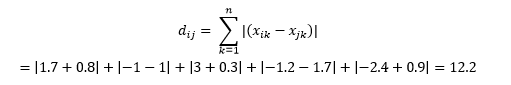
قد يكون هذا مفيدًا في بعض التطبيقات حيث يتم استخدام المسافة بالمعنى المادي الحقيقي بدلاً من إحساس التعلم الآلي "بالاختلاف". على سبيل المثال ، إذا كنت بحاجة إلى حساب المسافة التي تقطعها شاحنة الإطفاء للوصول إلى نقطة ما ، فإن استخدام هذا يكون أكثر عملية.

مسافة كانبرا هي البديل المرجح لمسافة مانهاتن ، ويتم حسابها على شكل

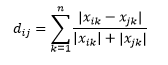
المسافة المعيارية L هي امتداد لما فوق اثنين - أو يمكنك القول أن الحالتين المذكورتين أعلاه هما حالتان محددتان لمسافة L- المعيارية - ويتم تعريفها على أنها

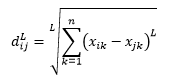
حيث L هو عدد صحيح موجب. لم أصادف أي حالات احتجت فيها إلى استخدام هذا ، ولكن لا يزال من الجيد معرفة الاحتمال. على سبيل المثال ، ستكون المسافة 3-معيار

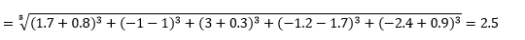
لاحظ أن L يجب أن تكون عددًا صحيحًا بشكل عام لأننا لا نريد إلغاء مساهمات المسافة الموجبة أو السالبة.

مسافة Minkowski هي تعميم لمسافة L- المعيارية ، حيث يمكن أن تأخذ L أي قيمة من 0 لتضمين القيم الكسرية. يتم تعريف مسافة Minkowski من أجل p على أنها

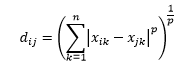
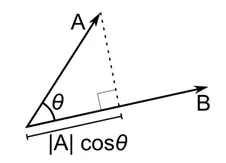
مسافة جيب التمام هي قياس الزاوية بين متجهين ، يمثل كل منهما ملاحظتين ، وتتشكل من خلال ضم نقطة البيانات إلى الأصل. تتراوح مسافة جيب التمام من 0 (نفس الشيء تمامًا) إلى 1 (لا يوجد اتصال) ، ويتم حسابها كـ

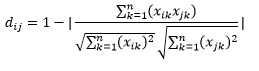
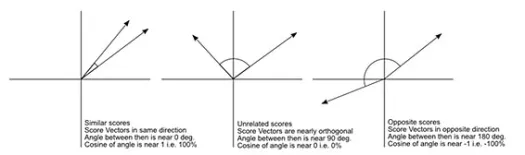
في حين أن هذا هو مقياس المسافة الأكثر شيوعًا عند العمل مع البيانات الفئوية ، يمكن أيضًا تعريف هذا للمتجه العددي. بالنسبة إلى متجهاتنا الرقمية ، سيكون هذا

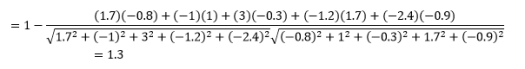
لكن ضع في اعتبارك التحذيرات ...

كنت تعلم أن هذا قادم ، أليس كذلك؟ إذا كانت التحليلات مجرد مجموعة من الصيغ الرياضية ، فلن نحتاج إلى أشخاص أذكياء مثلك للقيام بذلك.

أول شيء يجب ملاحظته هو أن المسافات المحسوبة بواسطة مقاييس مختلفة مختلفة. قد تميل إلى الاعتقاد بأن مسافة جيب التمام 1.3 هي الأصغر ، وبالتالي تشير إلى أن المتجهات هي الأقرب ولكن هذه ليست الطريقة الصحيحة للتفسير. لا يمكن مقارنة المسافات عبر الطرق المختلفة ، ويمكن فقط مقارنة المسافات بين أزواج مختلفة من الملاحظات تحت نفس الطريقة. المسافات لها معنى نسبي وليس لها معنى مطلق في حد ذاتها .

يؤدي هذا إلى السؤال التالي حول كيفية تحديد مقياس المسافة الصحيحة. لسوء الحظ ، لا توجد إجابة حقيقية. اعتمادًا على نوع البيانات والسياق ومشكلة العمل والتطبيق وطريقة التدريب النموذجية ، يعطي المقياس المختلف نتائج مختلفة. سيتعين عليك استخدام الحكم أو وضع افتراضات أو اختبار أداء النموذج لاتخاذ قرار بشأن المقياس الصحيح .

التحذير الثاني هو التحذير الذي أعيده كثيرًا عن لعنة الأبعاد. في الأبعاد الأعلى ، لا تتصرف المسافات بالطريقة التي نعتقد أنها تتصرف بها حدسيًا ، ويجب أن يكون المحلل حذرًا للغاية عند استخدام أي مقياس.

التحذير الثالث يتعلق بالعلاقة بين المسافات بين الملاحظات الثلاثة. تدعم بعض المقاييس عدم مساواة المثلث بينما لا يدعمها البعض الآخر . تشير عدم مساواة المثلث إلى أنه من الأقصر دائمًا الانتقال من النقطة i إلى النقطة j مباشرةً ، بدلاً من الانتقال عبر أي نقطة وسيطة k. رياضيا

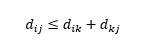
اعتمادًا على التطبيق الخاص بك ، قد تكون هذه الخاصية مطلوبة لمقياس المسافة وقد لا تكون كذلك.

أوه ، شيء آخر ، "المسافة" هي عكس "التشابه". كلما زادت المسافة ، قل التشابه والعكس صحيح. تعمل خوارزميات التجميع على المسافات ، وتعمل خوارزميات التوصية على التشابه ، لكنها في الأساس تتحدث عن نفس الشيء.

إذن ، كيف يمكنك تحويل رقم المسافة إلى رقم تشابه؟