Fluch der Dimensionalität
Veröffentlicht: 2015-07-08Was ist der Fluch der Dimensionalität?
Der Fluch der Dimensionalität bezieht sich auf nicht intuitive Eigenschaften von Daten, die bei der Arbeit im hochdimensionalen Raum* beobachtet werden, insbesondere in Bezug auf die Verwendbarkeit und Interpretation von Entfernungen und Volumina. Dies ist eines meiner Lieblingsthemen im maschinellen Lernen und in der Statistik, da es breite Anwendungen hat (nicht spezifisch für eine maschinelle Lernmethode), sehr kontraintuitiv und daher beeindruckend ist, eine tiefgreifende Anwendung für alle Analysetechniken bietet und es hat einen 'coolen' gruseligen Namen wie ein ägyptischer Fluch!
Betrachten Sie zum schnellen Verständnis dieses Beispiel: Angenommen, Sie haben eine Münze auf eine 100-Meter-Linie fallen lassen. Wie findest Du es? Ganz einfach, gehen Sie einfach auf die Linie und suchen Sie. Aber was ist, wenn es 100 x 100 Quadratmeter sind? Bereich? Es wird schon schwierig, einen (ungefähr) Fußballplatz nach einer einzigen Münze zu durchsuchen. Aber was ist, wenn es 100 x 100 x 100 Kubikmeter groß ist?! Weißt du, der Fußballplatz hat jetzt eine Höhe von dreißig Stockwerken. Viel Glück beim Finden einer Münze! Das ist im Wesentlichen der „Fluch der Dimensionalität“.
Viele ML-Methoden verwenden Distance Measure
Die meisten Segmentierungs- und Clustering -Methoden beruhen auf der Berechnung von Abständen zwischen Beobachtungen. Die bekannte k-Means-Segmentierung weist dem nächstgelegenen Zentrum Punkte zu. DBSCAN und hierarchisches Clustering erforderten ebenfalls Entfernungsmetriken. Verteilungs- und dichtebasierte Algorithmen zur Erkennung von Ausreißern verwenden auch den Abstand relativ zu anderen Abständen, um Ausreißer zu markieren.
Überwachte Klassifizierungslösungen wie die Methode k-Nearest Neighbors verwenden auch die Entfernung zwischen Beobachtungen, um unbekannten Beobachtungen eine Klasse zuzuweisen. Bei der Support Vector Machine- Methode werden Beobachtungen um ausgewählte Kernel herum transformiert, basierend auf dem Abstand zwischen der Beobachtung und dem Kernel.
Eine übliche Form von Empfehlungssystemen beinhaltet eine entfernungsbasierte Ähnlichkeit zwischen Benutzer- und Gegenstandsattributvektoren. Auch wenn andere Formen von Distanzen verwendet werden, spielt die Anzahl der Dimensionen eine Rolle im analytischen Design.
Eine der gebräuchlichsten Entfernungsmetriken ist die euklidische Entfernungsmetrik, die einfach die lineare Entfernung zwischen zwei Punkten im mehrdimensionalen Hyperraum ist. Der euklidische Abstand für Punkt i und Punkt j im n-dimensionalen Raum kann wie folgt berechnet werden:
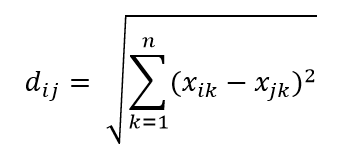
Distanz spielt Chaos in hoher Dimension
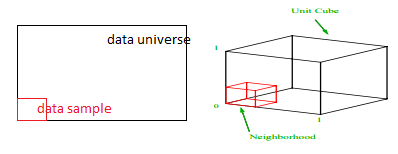
Betrachten Sie einen einfachen Prozess der Datenabtastung. Angenommen, das schwarze äußere Kästchen in Abb. 1 ist ein Datenuniversum mit gleichmäßiger Verteilung von Datenpunkten über das gesamte Volumen, und wir möchten 1 % der Beobachtungen abtasten, die von einem roten inneren Kästchen umschlossen sind. Black Box ist ein Hyperwürfel im mehrdimensionalen Raum, wobei jede Seite den Wertebereich in dieser Dimension darstellt. Für ein einfaches 3-dimensionales Beispiel in Abb. 1 haben wir möglicherweise den folgenden Bereich:
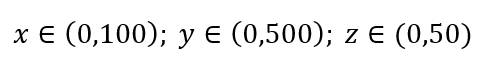
Abbildung 1: Probenahme
Welchen Anteil jedes Bereichs sollten wir abtasten, um diese 1 %-Stichprobe zu erhalten? Bei 2 Dimensionen erreichen 10 % des Bereichs eine Gesamtstichprobe von 1 %, sodass wir x∈(0,10) und y∈(0,50) auswählen und erwarten können, 1 % aller Beobachtungen zu erfassen. Denn 10%2=1%. Erwarten Sie, dass dieser Anteil für 3-dimensional höher oder niedriger sein wird?
Auch wenn unsere Suche jetzt in eine andere Richtung geht, steigt der Anteil tatsächlich auf 21,5 %. Und nicht nur vergrößert, sondern verdoppelt sich für nur eine zusätzliche Dimension! Und Sie können sehen, dass wir fast ein Fünftel jeder Dimension abdecken müssen, nur um ein Hundertstel des Gesamtwertes zu erhalten! In 10-Dimensionen beträgt dieser Anteil 63 % und in 100-Dimensionen – was keine ungewöhnliche Anzahl von Dimensionen in jedem realen maschinellen Lernen ist – muss man 95 % des Bereichs entlang jeder Dimension abtasten, um 1 % der Beobachtungen abzutasten! Dieses verblüffende Ergebnis tritt auf, weil die Streuung von Datenpunkten in hohen Dimensionen größer wird, selbst wenn sie gleichmäßig verteilt sind.

Dies hat Konsequenzen in Bezug auf das Design des Experiments und die Probenahme. Der Prozess wird sehr rechenaufwändig, selbst in dem Maße, in dem sich die Stichprobe asymptotisch der Population annähert, obwohl die Stichprobengröße viel kleiner als die Population bleibt.
Betrachten Sie eine weitere große Folge der hohen Dimensionalität. Viele Algorithmen messen die Distanz zwischen zwei Datenpunkten, um eine Art von Nähe (DBSCAN, Kernels, k-Nearest Neighbour) in Bezug auf einen vordefinierten Distanzschwellenwert zu definieren. In 2-Dimensionen können wir uns vorstellen, dass zwei Punkte nahe beieinander liegen, wenn einer in einen bestimmten Radius eines anderen fällt. Betrachten Sie das linke Bild in Abb. 2. Welcher Anteil der gleichmäßig verteilten Punkte innerhalb des schwarzen Quadrats fällt in den roten Kreis? Das ist ungefähr
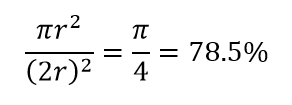
Abbildung 2: Nähe
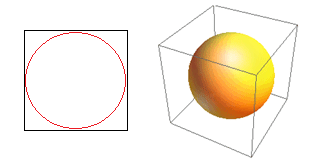
Wenn Sie also den größtmöglichen Kreis in das Quadrat einfügen, decken Sie 78 % des Quadrats ab. Die größtmögliche Kugel innerhalb des Würfels deckt jedoch nur ab
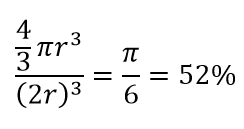
des Volumens. Dieses Volumen reduziert sich exponentiell auf 0,24 % für nur 10 Dimensionen! Was es im Wesentlichen bedeutet, dass sich in der hochdimensionalen Welt jeder einzelne Datenpunkt an Ecken befindet und nichts wirklich das Zentrum des Volumens ist, oder mit anderen Worten, das Zentrumsvolumen reduziert sich auf nichts, weil es (fast) kein Zentrum gibt! Dies hat enorme Konsequenzen für entfernungsbasierte Clustering-Algorithmen. Alle Entfernungen fangen an, gleich auszusehen, und jede Entfernung, die mehr oder weniger als eine andere ist, ist eher eine zufällige Schwankung der Daten als ein Maß für die Unähnlichkeit!
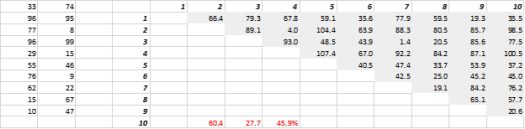
Fig. 3 zeigt zufällig erzeugte 2-D-Daten und entsprechende Alle-zu-Alle-Distanzen. Der Variationskoeffizient der Entfernung, berechnet als Standardabweichung dividiert durch den Mittelwert, beträgt 45,9 %. Die entsprechende Anzahl ähnlich erzeugter 5-D-Daten beträgt 26,5 % und für 10-D 19,1 %. Zugegeben, dies ist eine Probe, aber der Trend stützt die Schlussfolgerung, dass in hohen Dimensionen jede Entfernung ungefähr gleich ist und keine nah oder fern ist!
Abbildung 3: Distanz-Clustering
Hohe Dimension wirkt sich auch auf andere Dinge aus
Abgesehen von Abständen und Volumina schafft die Anzahl der Dimensionen andere praktische Probleme. Die Anforderungen an die Laufzeit der Lösung und den Systemspeicher steigen oft nichtlinear mit zunehmender Anzahl von Dimensionen. Aufgrund der exponentiellen Zunahme zulässiger Lösungen können viele Optimierungsverfahren globale Optima nicht erreichen und müssen sich mit lokalen Optima begnügen. Außerdem muss die Optimierung anstelle einer Lösung in geschlossener Form suchbasierte Algorithmen wie Gradientenabstieg, genetischer Algorithmus und simuliertes Glühen verwenden. Mehr Dimensionen führen zu Korrelationsmöglichkeiten, und die Parameterschätzung kann bei Regressionsansätzen schwierig werden.
Umgang mit High-Dimension
Dies wird an sich ein separater Blogbeitrag sein, aber Korrelationsanalyse, Clustering, Informationswert, Varianzinflationsfaktor, Hauptkomponentenanalyse sind einige der Möglichkeiten, wie die Anzahl der Dimensionen reduziert werden kann.
* Die Anzahl der Variablen, Beobachtungen oder Merkmale, aus denen ein Datenpunkt besteht, wird als Datendimension bezeichnet. Beispielsweise kann jeder Punkt im Raum mit 3 Koordinaten Länge, Breite und Höhe dargestellt werden und hat 3 Dimensionen
