Dichteschätzung mit Histogrammen

Wahrscheinlichkeitsdichtefunktionen (PDFs) beschreiben die Wahrscheinlichkeit, eine kontinuierliche Zufallsvariable in einem bestimmten Bereich des Raums zu beobachten. Erinnern Sie sich, dass PDF f(x) für eine eindimensionale Zufallsvariable X den Eigenschaften that folgt

Wahrscheinlichkeit, dass die Variable Werte zwischen annimmt

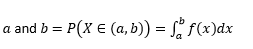
Wahrscheinlichkeit, dass die Variable Werte genau gleich annimmt

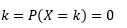
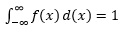
Das Schätzen eines solchen PDF aus einer Stichprobe von Beobachtungen ist ein häufiges Problem beim maschinellen Lernen. Dies ist bei vielen Algorithmen zur Erkennung von Ausreißern praktisch, bei denen wir versuchen, die „wahre“ Verteilung basierend auf Stichprobenbeobachtungen zu schätzen und dann einige der bestehenden oder neuen Beobachtungen als Ausreißer zu klassifizieren oder nicht. Zum Beispiel könnte ein Autoversicherer, der daran interessiert ist, Betrug aufzudecken, die Forderung nach Schadenshöhe für jede Art von Karosseriearbeiten prüfen, z. B. Stoßstangenersatz, und jeden zu hohen Betrag als potenziellen Betrug markieren. Als weiteres Beispiel kann ein Kinderpsychologe die Zeit untersuchen, die benötigt wird, um eine bestimmte Aufgabe bei verschiedenen Kindern zu erledigen, und diejenigen Kinder markieren, die zu lange oder zu kurze Zeit für eine mögliche Untersuchung benötigen.

In diesem Blogbeitrag erörtern wir, wie wir das PDF aus einer Stichprobe von Beobachtungen lernen können, damit wir die Wahrscheinlichkeit für jede Beobachtung berechnen und entscheiden können, ob es sich um ein häufiges oder seltenes Vorkommen handelt.

Dichteschätzung mit Histogramm

Zuerst generieren wir einige zufällige Daten zur Demonstration.

set.seed(123)
data <- c(rnorm(200, 10, 20), rnorm(200, 60, 30), runif(200, 120, 180)) # 600 points

Als nächstes visualisieren wir sie für unser Verständnis mithilfe eines Histogramms, wie in Abbildung 1.

# Plot 1
hist(data, breaks=50, freq=F, main="Univariate Distribution", xlab="Data Value")
# Plot 2
hist(data, breaks=20, freq=F, main="", xlab="20 Data Bins", col='red', border='red')
par(new=T)
hist(data, breaks=100, freq=F, main="Univariate Distribution", xlab=NULL, xaxt='n', yaxt='n')

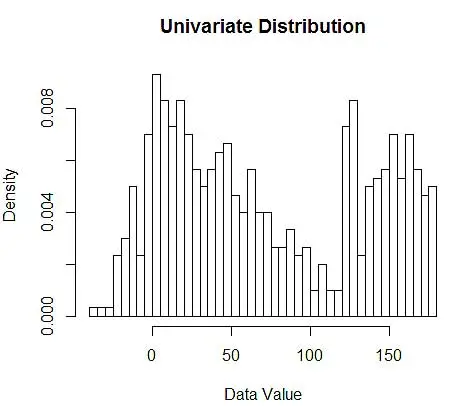
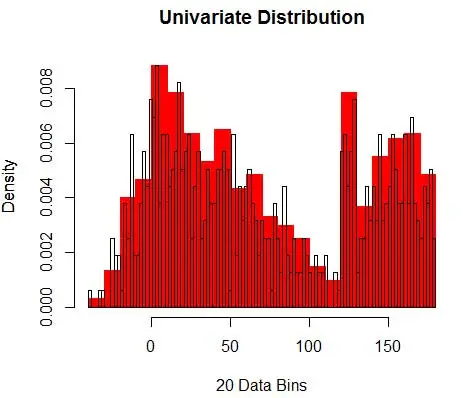
Während Histogramme Diagramme zur Datenvisualisierung sind, können Sie auch sehen, dass sie unsere erste Schätzung der Dichte sind. Genauer gesagt können wir die Dichte schätzen, indem wir die Daten in Bins unterteilen und annehmen, dass die Dichte innerhalb dieses Bin-Bereichs konstant ist und einen Wert hat, der gleich der Anzahl der Beobachtungen ist, die in diesen Bin fallen, als Anteil an der Gesamtzahl der Beobachtungen

Daher ist geschätztes PDF

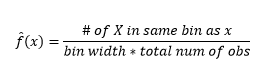
Und Sie stellen fest, dass Sie eine Annahme über die Bin-Breite getroffen haben, die sich auf die Dichteschätzung auswirkt. Daher ist die Bin-Breite ein Parameter für das Dichteschätzungsmodell unter Verwendung des Histogramms . Allerdings wird übersehen, dass wir auch mit einem weiteren Parameter arbeiten – nämlich der Startposition des ersten Bins . Sie können sehen, wie sich dies auf die Dichteschätzungen für alle Bins auswirken kann. Um den Einfluss der Bin-Breite zu sehen, überlagert Abbildung 2 Dichteschätzungen mit 20-Bin- und 100-Bin-Histogrammen. Betrachten Sie den eingekreisten Bereich, in dem weniger/gröbere Bins eine flache Dichteschätzung ergeben, während viele/feinere Bins eine unterschiedliche Dichteschätzung ergeben. Für den gelben Punkt reichen die Dichteschätzungen von 0,004 bis 0,008 aus zwei verschiedenen Modellen.

Daher ist die richtige Auswahl der Parameter entscheidend, um die Dichteschätzung richtig zu machen. Wir kommen darauf zurück, aber beachten Sie, dass es auch andere Probleme mit Histogrammen gibt. Dichteschätzungen unter Verwendung von Histogrammen sind ziemlich ruckartig und diskontinuierlich . Die Dichte ist für einen Behälter flach und ändert sich dann plötzlich drastisch für einen Punkt infinitesimal außerhalb des Behälters. Dies macht die Folgen einer falschen Schätzung für praktische Probleme noch schlimmer.

Schließlich haben wir zur besseren Veranschaulichung mit eindimensionalen Variablen gearbeitet, aber in der Praxis sind die meisten Probleme mehrdimensional. Da die Anzahl der Bins exponentiell mit der Anzahl der Dimensionen wächst, wächst auch die Anzahl der Beobachtungen, die zum Schätzen der Dichte erforderlich sind . Tatsächlich ist es plausibel, dass trotz Millionen von Beobachtungen viele Bins leer bleiben oder einstellige Beobachtungen enthalten. Mit nur jeweils 50 Bins in nur 3 Dimensionen haben wir 503 = 125000 Zellen, die gefüllt werden müssen. Das ergibt ungefähr durchschnittlich 8 Beobachtungen pro Zelle, wenn man eine gleichmäßige Verteilung annimmt, eine Million Beobachtungstrainingsdaten.

Wie wähle ich die richtigen Parameter aus?

Für Bin-Breite ist n die Anzahl der Beobachtungen N, für Bin J der Anteil der Beobachtungen

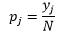
und Dichteschätzung ist

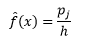
Die statistische Theorie beweist, dass, während f(x) der erwartete Wert der Dichte im Bin ist, die Varianz der Dichte es ist

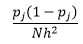
Während wir eine bessere Dichteschätzung erhalten können, indem wir die Bin-Breite n reduzieren, erhöhen wir die Varianz der Schätzung, da wir intuitiv eine zu feine Bin-Breite spüren können. Wir können die Methode der Kreuzvalidierung ohne Ausnahme verwenden, um den optimalen Satz von Parametern zu schätzen. Wir können die Dichte unter Verwendung aller Beobachtungen bis auf eine schätzen und dann die Dichte dieser ausgelassenen Beobachtung berechnen und den Schätzfehler messen. Das mathematische Auflösen für Histogramme ergibt eine Lösung in geschlossener Form für die Verlustfunktion für eine gegebene Bin-Breite.

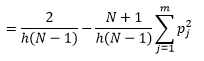
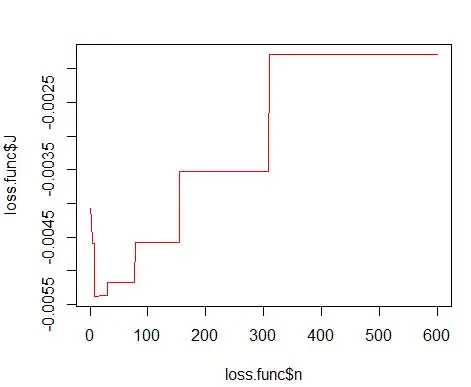
wobei m die Anzahl der Behälter ist. Technische Details dazu finden Sie in dieser Vorlesung [pdf] . Wir können diese Verlustfunktion für verschiedene Anzahlen von Behältern darstellen (Abbildung 3).

getLoss <- function(n.break) {
N <- 600
res <- hist(data, breaks=n.break, freq=F)
bin <- as.numeric(res$breaks)
h <- bin[2]-bin[1]
p <- res$density
p <- p * h
return ( 2/(h*(N-1)) - ( (N+1)/(h*(N-1))*sum(p*p) ) )
}
loss.func <- data.frame(n=1:600)
loss.func$J <- sapply(loss.func$n, function(x) getLoss(x))
# Plot 3
plot(loss.func$n, loss.func$J, col='red', type='l')
opt.break <- max(loss.func[loss.func$J == min(loss.func$J), 'n'])
print(opt.break)
# Plot 4
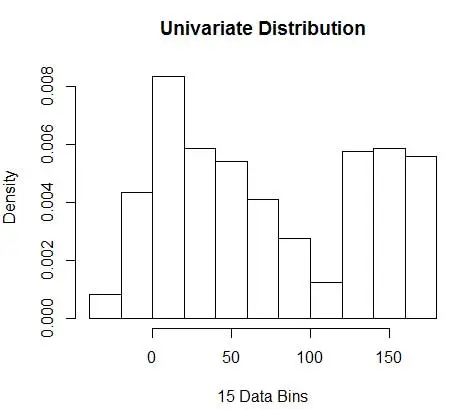
hist(data, breaks=opt.break, freq=F, main="Univariate Distribution", xlab="15 Data Bins")

und erhalten Sie die optimale Zahl als 15. Eigentlich ist alles zwischen 8 und 15 in Ordnung.

Folglich ist unter Abbildung 4 eine Dichteschätzung, die Dichtewerte sowie Granularität (mit optimalem Bias-Varianz-Kompromiss) ausgleicht.

Wenn Sie sich an dieser Stelle etwas unwohl fühlen, dann bin ich bei Ihnen. Auch wenn die Anzahl der Bins mathematisch optimal ist, scheint es eine zu grobe Schätzung zu sein. Es gibt kein intuitives Gefühl, warum wir die beste Arbeit geleistet haben. Und nicht zu vergessen andere Bedenken hinsichtlich der Ausgangsposition, der diskontinuierlichen Schätzung und des Fluchs der Dimensionalität. Verzweifeln Sie nicht, es gibt einen besseren Weg. Im nächsten Beitrag werden wir über die Dichteschätzung mit Kernels sprechen.