Entfernungsmessung im Hyperraum

Jeder, der sich nur oberflächlich mit Analysetechniken auskennt, hätte viele Algorithmen bemerkt, die sich für ihre Anwendung auf Abstände zwischen Datenpunkten verlassen. Jede Beobachtung oder Dateninstanz wird normalerweise als mehrdimensionaler Vektor dargestellt, und die Eingabe in den Algorithmus erfordert Abstände zwischen jedem Paar solcher Beobachtungen.

Die Entfernungsberechnungsmethode hängt von der Art der Daten ab – numerisch, kategorial oder gemischt. Einige der Algorithmen gelten nur für eine Klasse von Beobachtungen, während andere an mehreren arbeiten. In diesem Beitrag werden wir Distanzmaße diskutieren, die mit numerischen Daten arbeiten. Es gibt vielleicht mehr Möglichkeiten, Entfernungen im multidimensionalen Hyperraum zu messen, als diese in einem einzigen Blogbeitrag behandelt werden können, und man kann immer neue Wege erfinden, aber wir sehen uns einige der gängigen Entfernungsmetriken und ihre relativen Vorzüge an.

Für den Rest des Blogbeitrags implizieren wir

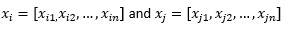
sich auf zwei Beobachtungen oder Datenvektoren zu beziehen.

Zuerst die Daten vorbereiten…

Bevor wir verschiedene Entfernungsmetriken überprüfen, müssen wir die Daten vorbereiten:

Umwandlung in numerischen Vektor

Bei einer gemischten Beobachtung, die sowohl numerische als auch kategoriale Dimensionen enthält, besteht der erste Schritt darin, die kategoriale Dimension tatsächlich in numerische Dimension(en) umzuwandeln. Eine kategoriale Dimension mit drei möglichen Werten kann in zwei oder drei numerische Dimensionen mit binären Werten umgewandelt werden. Da diese kategoriale Variable notwendigerweise einen von drei Werten annimmt, wird eine von drei numerischen Dimensionen perfekt mit den anderen zwei korrelieren. Dies kann je nach Anwendung in Ordnung sein oder nicht.

Wenn die Beobachtung rein kategorial ist, wie z. B. eine Textzeichenfolge (Sätze unterschiedlicher Länge) oder eine Genomsequenz (Sequenzen fester Länge), kann eine spezielle Distanzmetrik direkt angewendet werden, ohne Daten in ein numerisches Format umzuwandeln. Wir werden diese Algorithmen im nächsten Beitrag besprechen.

Normalisierung

Abhängig von Ihrem Anwendungsfall möchten Sie möglicherweise jede Dimension auf derselben Skala normalisieren, damit der Abstand entlang einer Dimension den Gesamtabstand zwischen Beobachtungen nicht übermäßig beeinflusst. Dasselbe wurde im k-Means-Algorithmus diskutiert. Es sind zwei Arten der Normalisierung möglich:

Die Bereichsnormalisierung (Neuskalierung) normalisiert Daten so, dass sie im Bereich von 0 bis 1 liegen, indem der Mindestwert von jeder Dimension subtrahiert und dann durch den Wertebereich in dieser Dimension dividiert wird.

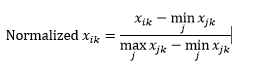
Das erste Problem bei der Bereichsnormalisierung besteht darin, dass ein unsichtbarer Wert über den Bereich von 0–1 hinaus normalisiert werden kann. Dies ist zwar im Allgemeinen kein Problem für die meisten Entfernungsmetriken, aber wenn der Algorithmus negative Werte nicht verarbeiten kann, kann dies ein Problem darstellen. Das zweite Problem ist, dass dies stark von Ausreißern abhängt. Wenn eine Beobachtung einen sehr extremen (hohen oder niedrigen) Wert für eine Dimension hat, werden die normalisierten Werte für diese Dimension für andere Beobachtungen zusammengedrängt und verlieren ihre Unterscheidungskraft.

Die Standardnormalisierung (Z-Skalierung) normalisiert die Dimension auf einen Mittelwert von 0 und eine Standardabweichung von 1, indem der Mittelwert von dieser Dimension jeder Beobachtung subtrahiert und dann durch die Standardabweichung des Werts dieser Dimension über alle Beobachtungen geteilt wird.

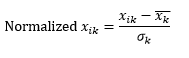
Dies hält die Daten im Allgemeinen ungefähr im Bereich von -5 bis +5 und vermeidet den Einfluss von Extremwerten.

Wir haben die Z-Skalierung von zwei Beobachtungen simuliert. Simuliert, weil wir wirklich viel mehr als zwei Beobachtungen benötigen, um den Mittelwert und die Standardabweichung jeder Dimension zu berechnen, und wir hier beide Zahlen für jede Dimension angenommen haben.

Dann berechne die Distanz...

Die euklidische Distanz – auch Luftlinie genannt – ist die kürzeste Distanz im multidimensionalen Hyperraum zwischen zwei Punkten. Sie kennen dies aus der 2D-Ebene oder dem 3D-Raum (dies ist eine Linie), aber ein ähnliches Konzept erstreckt sich auf höhere Dimensionen. Der euklidische Abstand zwischen Vektoren im n-dimensionalen Raum wird berechnet als

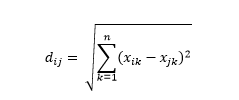
Für transformierte Datenvektorbeispiele ist dies

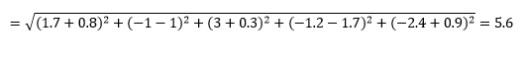
Dies ist die gebräuchlichste Metrik und für die meisten Anwendungen oft sehr gut geeignet. Eine Variante davon ist die quadrierte euklidische Distanz, die nur die Summe der quadrierten Differenzen ist.

Die Manhattan-Distanz – benannt nach der rasterähnlichen Struktur der Straßen von Manhattan in New York in Ost-West-Nord-Süd – ist die Entfernung zwischen zwei Punkten, wenn sie parallel zu den Achsen verlaufen.

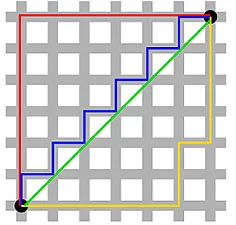
Manhattan-Entfernung
Euklidische Entfernung

Dies wird berechnet als

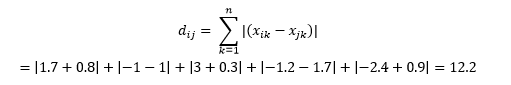
Dies kann in einigen Anwendungen nützlich sein, in denen Entfernung im realen, physischen Sinne verwendet wird und nicht im Sinne des maschinellen Lernens von „Unähnlichkeit“. Wenn Sie beispielsweise die Entfernung berechnen müssen, die ein Feuerwehrauto zurücklegt, um einen Punkt zu erreichen, ist dies praktischer.

Die Canberra-Distanz ist eine gewichtete Variante der Manhattan-Distanz und wird wie folgt berechnet

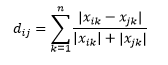
Die L-Norm-Distanz ist die Erweiterung von über zwei – oder man kann sagen, dass die über zwei spezifische Fälle der L-Norm-Distanz sind – und ist definiert als

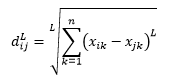
wobei L eine positive ganze Zahl ist. Ich bin auf keine Fälle gestoßen, in denen ich dies verwenden musste, aber dies ist immer noch gut zu wissen, dass es möglich ist. Zum Beispiel wird 3-Norm-Abstand sein

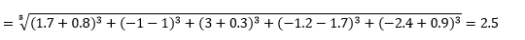
Beachten Sie, dass L im Allgemeinen eine gerade ganze Zahl sein sollte, da wir nicht möchten, dass sich positive oder negative Distanzbeiträge aufheben.

Die Minkowski-Distanz ist eine Verallgemeinerung der L-Norm-Distanz, wobei L jeden Wert von 0 bis einschließlich Bruchwerten annehmen kann. Minkowski-Abstand der Ordnung p ist definiert als

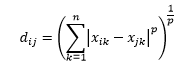
Der Kosinusabstand ist ein Maß für den Winkel zwischen zwei Vektoren, die jeweils zwei Beobachtungen darstellen und durch Verbinden von Datenpunkten mit dem Ursprung gebildet werden. Der Kosinusabstand reicht von 0 (genau gleich) bis 1 (keine Verbindung) und wird berechnet als

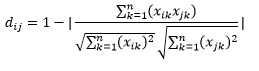
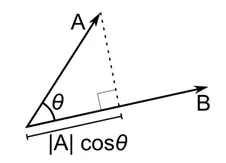
Während dies bei der Arbeit mit kategorialen Daten ein häufigeres Distanzmaß ist, kann es auch für numerische Vektoren definiert werden. Für unsere numerischen Vektoren wird dies sein

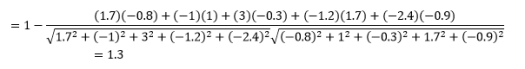
Aber beachten Sie die Einschränkungen …

Du wusstest, dass das kommen würde, oder? Wenn die Analytik nur ein Haufen mathematischer Formeln wäre, brauchen wir dafür keine schlauen Leute wie Sie.

Als Erstes ist zu beachten, dass Entfernungen, die mit unterschiedlichen Metriken berechnet werden, unterschiedlich sind. Sie könnten versucht sein zu glauben, dass der Kosinusabstand von 1,3 am kleinsten ist und daher darauf hinweist, dass die Vektoren am nächsten sind, aber dies ist nicht die richtige Interpretation. Distanzen zwischen verschiedenen Methoden können nicht verglichen werden, und nur Distanzen zwischen verschiedenen Paaren von Beobachtungen mit derselben Methode können verglichen werden. Entfernungen haben eine relative Bedeutung und keine absolute Bedeutung für sich .

Dies führt zur nächsten Frage, wie man die richtige Entfernungsmetrik auswählt. Leider gibt es darauf keine wahre Antwort. Je nach Datentyp, Kontext, Geschäftsproblem, Anwendung und Modelltrainingsmethode liefern verschiedene Metriken unterschiedliche Ergebnisse. Sie müssen Ihr Urteilsvermögen einsetzen, Annahmen treffen oder die Modellleistung testen, um sich für die richtige Metrik zu entscheiden .

Der zweite Vorbehalt ist mein oft wiederholter über den Fluch der Dimensionalität. In höheren Dimensionen verhalten sich Entfernungen nicht so, wie wir es uns intuitiv vorstellen , und Analysten müssen äußerst vorsichtig sein, wenn sie Metriken verwenden.

Der dritte Vorbehalt bezieht sich auf die Beziehung zwischen den Abständen zwischen drei Beobachtungen. Einige Metriken unterstützen die Dreiecksungleichung und andere nicht . Die Dreiecksungleichung impliziert, dass es immer am kürzesten ist, direkt von Punkt i zu Punkt j zu gelangen, anstatt über einen Zwischenpunkt k. Mathematisch,

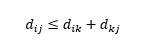
Abhängig von Ihrer Anwendung kann dies eine erforderliche Eigenschaft der Entfernungsmetrik sein oder nicht.

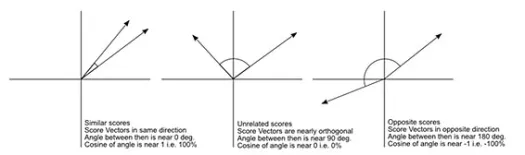
Oh, noch etwas, „Distanz“ ist das Gegenteil von „Ähnlichkeit“. Je größer der Abstand, desto geringer die Ähnlichkeit und umgekehrt. Clustering-Algorithmen arbeiten mit Entfernungen und Empfehlungsalgorithmen arbeiten mit Ähnlichkeiten, aber im Wesentlichen sprechen sie über dasselbe.

Wie können Sie also die Abstandszahl in eine Ähnlichkeitszahl umwandeln?