次元の呪い
公開: 2015-07-08次元の呪いとは何ですか
Curse of Dimensionalityは、高次元空間*で作業しているときに観察されるデータの非直感的なプロパティを指します。特に、距離とボリュームの使いやすさと解釈に関連しています。 これは、機械学習と統計で私のお気に入りのトピックの1つです。これは、幅広いアプリケーション(どの機械学習方法にも固有ではない)があり、非常に直感に反し、したがって畏敬の念を起こさせるものであり、あらゆる分析手法に深遠なアプリケーションがあるためです。エジプトの呪いのように「かっこいい」怖い名前が付いています!
すばやく把握するために、次の例を検討してください。たとえば、100メートルのラインにコインを落としたとします。 どうやって見つけますか? シンプルで、ラインを歩いて検索するだけです。 しかし、100x100平方メートルの場合はどうでしょうか。 分野? (大まかに)サッカー場で1枚のコインを探しようとして、すでに困難になっています。 しかし、100 x 100 x 100 cu.mのスペースだとしたらどうでしょうか?! ご存知のように、サッカー場の高さは30階建てになっています。 そこでコインを見つけて頑張ってください! つまり、本質的には「次元の呪い」です。
多くのMLメソッドは距離測定を使用します
ほとんどのセグメンテーションおよびクラスタリング手法は、観測間の距離の計算に依存しています。 よく知られているk-Meansセグメンテーションは、最も近い中心にポイントを割り当てます。 DBSCANおよび階層的クラスタリングにも距離メトリックが必要でした。 分布および密度ベースの外れ値検出アルゴリズムも、他の距離との相対距離を利用して外れ値をマークします。
k最近傍法のような教師あり分類ソリューションも、観測間の距離を使用して、クラスを未知の観測に割り当てます。 サポートベクターマシン方式では、観測値とカーネルの間の距離に基づいて、選択したカーネルの周囲の観測値を変換します。
レコメンデーションシステムの一般的な形式には、ユーザーとアイテムの属性ベクトル間の距離ベースの類似性が含まれます。 他の形式の距離が使用されている場合でも、分析設計では次元の数が影響します。
最も一般的な距離メトリックの1つは、ユークリッド距離メトリックです。これは、多次元ハイパースペース内の2点間の単純な線形距離です。 n次元空間の点iと点jのユークリッド距離は次のように計算できます。
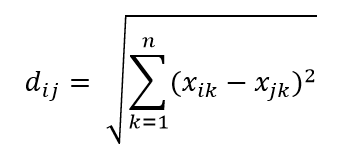
距離は高次元で大混乱を引き起こします
データサンプリングの簡単なプロセスを考えてみましょう。 図1の黒い外側のボックスが、ボリューム全体にデータポイントが均一に分布しているデータユニバースであり、赤い内側のボックスで囲まれた観測値の1%をサンプリングするとします。 ブラックボックスは多次元空間のハイパーキューブであり、各辺はその次元の値の範囲を表します。 図1の単純な3次元の例では、次の範囲があります。
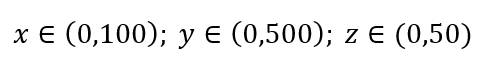
図1:サンプリング
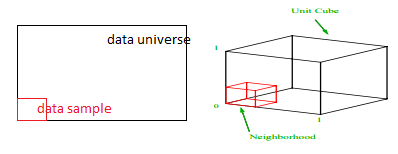
その1%のサンプルを取得するには、各範囲のどのくらいの割合をサンプリングする必要がありますか? 2次元の場合、範囲の10%で全体の1%のサンプリングが達成されるため、x∈(0,10)とy∈(0,50)を選択して、すべての観測値の1%をキャプチャすることを期待できます。 これは、10%2 = 1%であるためです。 この比率は、3次元で高くなると思いますか、それとも低くなると思いますか?
現在、検索は追加の方向に進んでいますが、比例は実際には21.5%に増加します。 そして、増加するだけでなく、1つの追加の次元のために、それは2倍になります! そして、全体の100分の1を取得するには、各次元のほぼ5分の1をカバーする必要があることがわかります。 10次元では、この割合は63%であり、100次元では、実際の機械学習では珍しいことではありませんが、観測値の1%をサンプリングするには、各次元に沿って範囲の95%をサンプリングする必要があります。 この気が遠くなるような結果は、高次元では、データポイントが均一に分散していても、データポイントの拡散が大きくなるために発生します。

これは、実験計画法とサンプリングの観点から重要です。 サンプルサイズが母集団よりはるかに小さいままであるにもかかわらず、サンプリングが漸近的に母集団に近づく程度でさえ、プロセスは非常に計算コストが高くなります。
高次元の別の大きな結果を考えてみましょう。 多くのアルゴリズムは、2つのデータポイント間の距離を測定して、事前定義された距離しきい値を参照して、ある種の近さ(DBSCAN、カーネル、k最近傍)を定義します。 2次元では、一方が他方の特定の半径内にある場合、2つの点が近くにあると想像できます。 図2の左側の画像を考えてみましょう。黒い四角の中に等間隔に配置された点が赤い円の中に入る割合はどれくらいですか。 それは約です
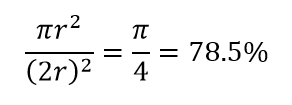
図2:近さ
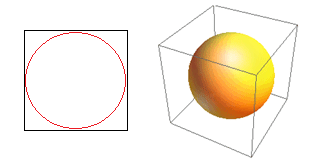
したがって、正方形の内側に可能な最大の円を収めると、正方形の78%をカバーします。 それでも、立方体内で可能な最大の球はカバーするだけです
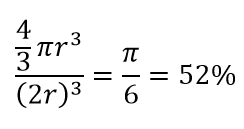
ボリュームの。 このボリュームは、わずか10次元で指数関数的に0.24%に減少します。 つまり、高次元の世界では、すべてのデータポイントがコーナーにあり、実際にはボリュームの中心には何もありません。つまり、(ほとんど)中心がないため、中心のボリュームはゼロになります。 これは、距離ベースのクラスタリングアルゴリズムに大きな影響を及ぼします。 すべての距離は同じように見え始め、他の距離よりも多かれ少なかれ距離は、非類似性の尺度ではなく、データのよりランダムな変動です!
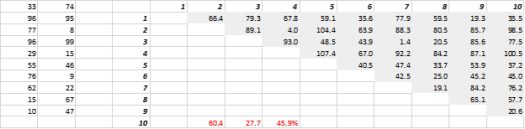
図3は、ランダムに生成された2Dデータと対応する全距離を示しています。 標準偏差を平均で割って計算した距離の変動係数は45.9%です。 同様に生成された5-Dデータの対応する数は26.5%であり、10-Dの場合は19.1%です。 確かにこれは1つのサンプルですが、傾向は、高次元ではすべての距離がほぼ同じであり、近くにも遠くにもないという結論を裏付けています。
図3:距離クラスタリング
高次元は他のものにも影響を及ぼします
距離と体積は別として、次元の数は他の実際的な問題を引き起こします。 ソリューションの実行時およびシステムメモリの要件は、多くの場合、次元数の増加に伴って非線形にエスカレートします。 実行可能なソリューションが指数関数的に増加するため、多くの最適化手法はグローバルな最適化に到達できず、ローカルな最適化を実行する必要があります。 さらに、最適化では、閉じた形式のソリューションの代わりに、最急降下法、遺伝的アルゴリズム、シミュレーテッドアニーリングなどの検索ベースのアルゴリズムを使用する必要があります。 より多くの次元は相関の可能性をもたらし、回帰アプローチではパラメーター推定が困難になる可能性があります。
高次元への対応
これ自体は別のブログ投稿になりますが、相関分析、クラスタリング、情報値、分散拡大係数、主成分分析は、次元数を減らすことができるいくつかの方法です。
*データポイントを構成する変数、観測値、または特徴の数は、データの次元と呼ばれます。 たとえば、空間内の任意のポイントは、長さ、幅、高さの3つの座標を使用して表すことができ、3つの次元があります。
