ヒストグラムを使用した密度推定

確率密度関数（PDF）は、空間のある領域で連続確率変数を観測する確率を表します。 1次元確率変数Xの場合、PDF f（x）が次のプロパティに従うことを思い出してください。

変数が次の値を取る確率

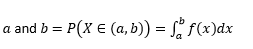
変数が正確に等しい値を取る確率

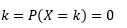
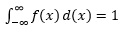
観測のサンプルからこのようなPDFを推定することは、機械学習でよくある問題です。 これは、サンプルの観測値に基づいて「真の」分布を推定し、既存または新規の観測値の一部を外れ値として分類する多くの外れ値検出アルゴリズムで役立ちます。 たとえば、詐欺を捕まえることに関心のある自動車保険会社は、バンパーの交換など、ボディワークのタイプごとに請求額の要求を調べ、高すぎる金額を詐欺の可能性があるとマークする場合があります。 別の例として、子供の心理学者は、さまざまな子供たちの間で特定のタスクを完了するのにかかる時間を調べ、潜在的な調査に時間がかかりすぎる、または短すぎる子供たちにマークを付けることができます。

このブログ投稿では、観測のサンプルからPDFを学習する方法について説明します。これにより、各観測の確率を計算し、それが一般的かまれかを判断できます。

ヒストグラムを使用した密度推定

まず、デモンストレーション用にランダムなデータを生成します。

set.seed(123)
data <- c(rnorm(200, 10, 20), rnorm(200, 60, 30), runif(200, 120, 180)) # 600 points

次に、図1のように、ヒストグラムを使用して、理解のためにそれらを視覚化します。

# Plot 1
hist(data, breaks=50, freq=F, main="Univariate Distribution", xlab="Data Value")
# Plot 2
hist(data, breaks=20, freq=F, main="", xlab="20 Data Bins", col='red', border='red')
par(new=T)
hist(data, breaks=100, freq=F, main="Univariate Distribution", xlab=NULL, xaxt='n', yaxt='n')

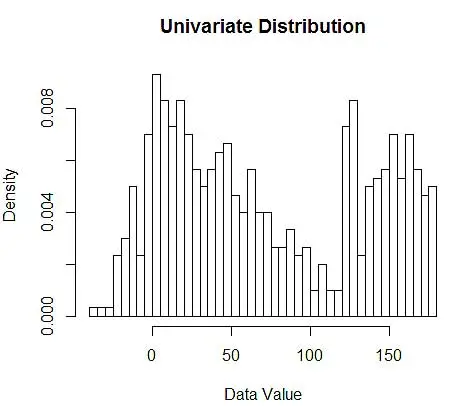
ヒストグラムはデータを視覚化するためのグラフですが、密度の最初の推定値であることがわかります。 より具体的には、データをビンに分割し、密度がそのビンの範囲内で一定であり、観測の総数の割合としてそのビンに分類される観測の数に等しい値を持つと仮定することにより、密度を推定できます。

したがって、推定PDFは

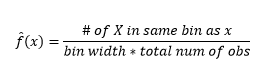
そして、密度推定に影響を与えるビン幅について仮定を立てたことに気づきます。 したがって、bin-widthは、ヒストグラムを使用した密度推定モデルのパラメーターです。 ただし、見落とされている事実は、最初のビンの開始位置であるもう1つのパラメーターも使用しているということです。 これがすべてのビンの密度推定にどのように影響するかを確認できます。 ビン幅の影響を確認するために、図2は、密度推定値を20ビンおよび100ビンのヒストグラムと重ね合わせています。 囲まれた領域を見てください。ここでは、ビンが少ない/粗い場合は密度推定がフラットになり、ビンが多い場合/密度が異なる場合は密度推定が異なります。 黄色の点の場合、密度の推定値は2つの異なるモデルから0.004から0.008の範囲になります。

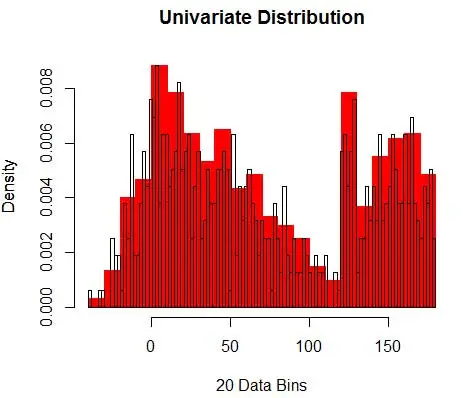
したがって、パラメータを正しく選択することは、密度の推定を正しく行うために重要です。 これについては説明しますが、ヒストグラムには他にも問題があることに注意してください。 ヒストグラムを使用した密度推定は、非常にぎくしゃくして不連続です。 密度はビンに対してフラットであり、その後、ビンの非常に外側のポイントで急激に変化します。 これにより、実際の問題では、誤った見積もりの​​結果がさらに悪化します。

最後に、説明を簡単にするために1次元変数を使用して作業しましたが、実際には、ほとんどの問題は多次元です。 ビンの数は次元の数とともに指数関数的に増加するため、密度を推定するために必要な観測の数も増加します。 実際、何百万もの観測値があるにもかかわらず、多くのビンが空のままであるか、1桁の観測値が含まれている可能性があります。 それぞれがわずか3次元で50個のビンがあるため、入力する必要のある503=125000セルがあります。 これは、均一な分布、100万の観測トレーニングデータを想定すると、セルあたり平均8つの観測になります。

適切なパラメータを選択する方法は？

ビン幅nの場合、観測数N、ビンJの場合、観測の割合は次のようになります。

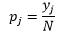
密度推定は

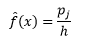
統計理論は、f（x）がビン内の密度の期待値であるのに対し、密度の分散は

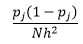
ビン幅nを減らすことでより良い密度推定を得ることができますが、ビン幅が細すぎることを直感的に感じることができるため、推定の分散を増やします。 Leave one-out cross-validation手法を使用して、最適なパラメーターのセットを推定できます。 1つを除くすべての観測値を使用して密度を推定し、次に、除外された観測値の密度を計算して、推定の誤差を測定できます。 これをヒストグラムについて数学的に解くと、与えられたビン幅の損失関数の閉じた形の解が得られます。

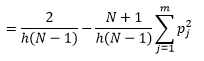
ここで、mはビンの数です。 上記の技術的な詳細は、この講義[pdf]にあります。 この損失関数をさまざまな数のビンに対してプロットできます（図3）

getLoss <- function(n.break) {
N <- 600
res <- hist(data, breaks=n.break, freq=F)
bin <- as.numeric(res$breaks)
h <- bin[2]-bin[1]
p <- res$density
p <- p * h
return ( 2/(h*(N-1)) - ( (N+1)/(h*(N-1))*sum(p*p) ) )
}
loss.func <- data.frame(n=1:600)
loss.func$J <- sapply(loss.func$n, function(x) getLoss(x))
# Plot 3
plot(loss.func$n, loss.func$J, col='red', type='l')
opt.break <- max(loss.func[loss.func$J == min(loss.func$J), 'n'])
print(opt.break)
# Plot 4
hist(data, breaks=opt.break, freq=F, main="Univariate Distribution", xlab="15 Data Bins")

最適な数は15になります。実際には8〜15の範囲で問題ありません。

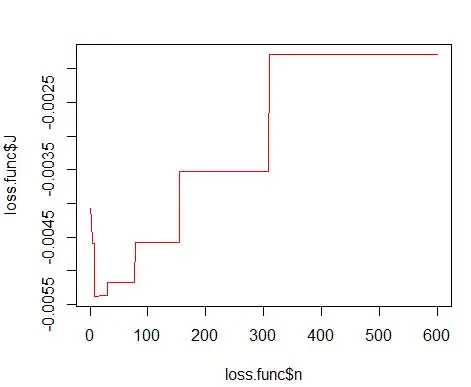
したがって、図4の下には、密度値と粒度のバランスをとる密度推定があります（最適なバイアス分散のトレードオフを使用）。

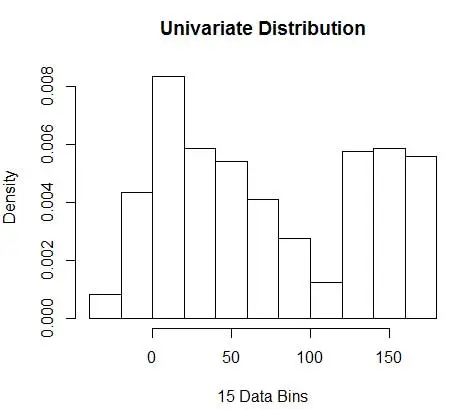
この時点で少し不安を感じるなら、私はあなたと一緒です。 ビンの数は数学的に最適ですが、見積もりが粗すぎるように感じます。 なぜ私たちが最高の仕事をしたのか、直感的な感覚はありません。 そして、開始位置、不連続な推定、および次元の呪いに関する他の懸念を忘れないでください。 失望しないでください、より良い方法があります。 次の投稿では、カーネルを使用した密度推定について説明します。