超空間での距離の測定
公開: 2016-01-10分析手法に大まかに精通している人なら誰でも、アプリケーションのデータポイント間の距離に依存するアルゴリズムがたくさんあることに気付くでしょう。 各観測値またはデータインスタンスは通常、多次元ベクトルとして表され、アルゴリズムへの入力には、そのような観測値の各ペア間の距離が必要です。
距離の計算方法は、データのタイプ(数値、カテゴリ、または混合)によって異なります。 一部のアルゴリズムは1つのクラスの観測にのみ適用されますが、他のアルゴリズムは複数のクラスで機能します。 この投稿では、数値データを処理する距離測度について説明します。 多次元ハイパースペースで距離を測定する方法は、単一のブログ投稿でカバーできる方法よりもおそらく多く、常に新しい方法を考案することができますが、一般的な距離メトリックとそれらの相対的なメリットのいくつかを調べます。
ブログ投稿の残りの目的のために、私たちは意味します
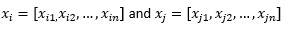
2つの観測値またはデータベクトルを参照します。
まず、データを準備します…
さまざまな距離メトリックを確認する前に、データを準備する必要があります。
数値ベクトルへの変換
数値次元とカテゴリ次元の両方を含む混合観測の場合、最初のステップは、実際にカテゴリ次元を数値次元に変換することです。 3つの潜在的な値を持つカテゴリディメンションは、バイナリ値を持つ2つまたは3つの数値ディメンションに変換できます。 このカテゴリ変数は必然的に3つの値のいずれかを取るため、3つの数値次元の1つは他の2つと完全に相関します。 これは、アプリケーションによっては問題ない場合とそうでない場合があります。

観測がテキスト文字列(さまざまな長さの文)やゲノムシーケンス(固定長のシーケンス)など、純粋にカテゴリ別である場合、データを数値形式に変換せずに、特別な距離メトリックを直接適用できます。 これらのアルゴリズムについては、次の投稿で説明します。
正規化
ユースケースによっては、各次元を同じスケールで正規化して、任意の1つの次元に沿った距離が観測間の全体的な距離に過度に影響を与えないようにすることができます。 同じことがk-Meansアルゴリズムでも議論されました。 可能な正規化には2種類あります。
範囲の正規化(再スケーリング)は、各ディメンションから最小値を減算し、そのディメンションの値の範囲で除算することにより、データを0から1の範囲に正規化します。
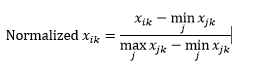
範囲の正規化に関する最初の問題は、見えない値が0-1の範囲を超えて正規化される可能性があることです。 ただし、これは通常、ほとんどの距離メトリックでは問題になりませんが、アルゴリズムが負の値を処理できない場合は、これが問題になる可能性があります。 2番目の問題は、これが外れ値に大きく依存していることです。 1つの観測値が次元に対して非常に極端な(高いまたは低い)値を持っている場合、他の観測値のその次元の正規化された値は一緒に群がり、識別力を失います。
標準正規化(zスケーリング)は、各観測値の次元から平均を差し引き、すべての観測値にわたるその次元の値の標準偏差で除算することにより、次元を正規化して平均0と標準偏差1にします。
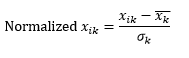
これにより、通常、データはおおよそ-5〜 + 5の範囲に保たれ、極値の影響を回避できます。
2つの観測値のzスケーリングをシミュレートしました。 シミュレートされたのは、各次元の平均と標準偏差を計算するために2つ以上の観測値が実際に必要であり、ここでは各次元についてこれらの数値の両方を想定しているためです。

次に、距離を計算します…
ユークリッド距離(別名「カラスが飛ぶとき」の距離)は、2点間の多次元超空間での最短距離です。 これは2D平面または3D空間(これは線です)でよく知っていますが、同様の概念がより高い次元に拡張されます。 n次元空間のベクトル間のユークリッド距離は次のように計算されます。
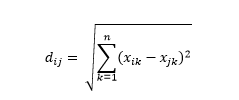
変換されたデータベクトルの例の場合、これは
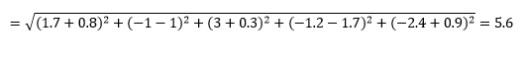
これは最も一般的なメトリックであり、多くの場合、ほとんどのアプリケーションに非常に適しています。 これの変形は、2乗されたユークリッド距離です。これは、2乗された差の合計です。
マンハッタン距離(ニューヨークのマンハッタンの通りの東西南北グリッドのような構造にちなんで名付けられました)は、軸に平行に移動するときの2点間の距離です。
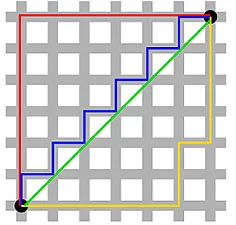
マンハッタン距離
ユークリッド距離

これは次のように計算されます
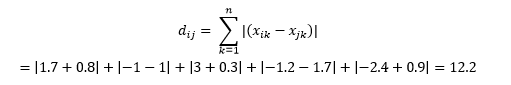
これは、機械学習の「非類似性」という意味ではなく、実際の物理的な意味で距離が使用されるアプリケーションで役立つ場合があります。 たとえば、消防車がポイントに到達するまでにかかる距離を計算する必要がある場合は、これを使用する方が実用的です。
キャンベラ距離はマンハッタン距離の加重バリアントであり、次のように計算されます。
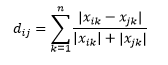
L-ノルム距離は2つ以上の延長であり、2つ以上はL-ノルム距離の特定のケースであると言えます。これは次のように定義されます。
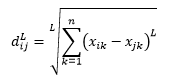
ここで、Lは正の整数です。 これを使用する必要があるケースはありませんが、それでも可能性を知るのは良いことです。 たとえば、3ノルムの距離は
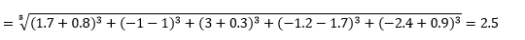
正または負の距離の寄与をキャンセルしたくないので、Lは一般に整数である必要があることに注意してください。
ミンコフスキー距離は、Lノルム距離の一般化であり、Lは0から小数値を含むまでの任意の値を取ることができます。 次数pのミンコフスキー距離は次のように定義されます。
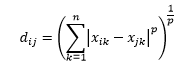

コサイン距離は、それぞれが2つの観測値を表す、2つのベクトル間の角度の尺度であり、データポイントを原点に結合することによって形成されます。 コサイン距離は0(まったく同じ)から1(接続なし)の範囲で、次のように計算されます。
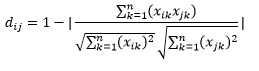
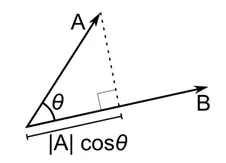
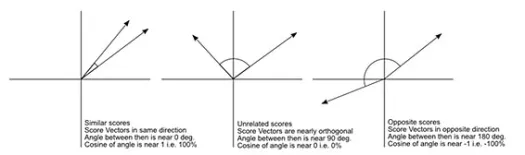
これは、カテゴリデータを操作する場合のより一般的な距離測定ですが、数値ベクトルに対しても定義できます。 数値ベクトルの場合、これは次のようになります。
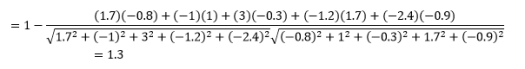
ただし、注意点に注意してください…
あなたはこれが来ることを知っていましたね? 分析が単なる数式の集まりである場合、あなたのような賢い人々がそれを行う必要はありません。
最初に注意することは、異なるメトリックによって計算された距離が異なることです。 1.3のコサイン距離が最小であり、したがってベクトルが最も近いことを示していると考えたくなるかもしれませんが、これは正しい解釈方法ではありません。 異なる方法間の距離を比較することはできず、同じ方法での異なる観測ペア間の距離のみを比較できます。 距離には相対的な意味があり、それ自体では絶対的な意味はありません。
これは、正しい距離メトリックを選択する方法の次の質問につながります。 残念ながら、本当の答えはありません。 データのタイプ、コンテキスト、ビジネス上の問題、アプリケーション、およびモデルのトレーニング方法に応じて、メトリックが異なれば結果も異なります。 適切なメトリックを決定するには、判断を使用するか、仮定を作成するか、モデルのパフォーマンスをテストする必要があります。
2番目の注意点は、次元の呪いについてよく繰り返される警告です。 高次元では、距離は直感的に考えられるようには動作しません。また、分析者は、メトリックを使用する場合は非常に注意する必要があります。
3番目の注意点は、3つの観測値間の距離の関係についてです。 一部のメトリックは三角不等式をサポートしますが、他のメトリックはサポートしません。 三角不等式は、中間点kを経由するのではなく、点iから点jに直接移動することが常に最短であることを意味します。 数学的には、
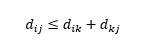
アプリケーションに応じて、これは距離メトリックの必須プロパティである場合とそうでない場合があります。
ああ、もう1つ、 「距離」は「類似性」の反対です。 距離が長くなるほど、類似性が低くなり、その逆も同様です。 クラスタリングアルゴリズムは距離で機能し、レコメンデーションアルゴリズムは類似性で機能しますが、基本的には同じことを話します。
では、どのようにして距離数を相似数に変換できますか?
