Maldición de dimensionalidad
Publicado: 2015-07-08¿Qué es la maldición de la dimensionalidad?
La maldición de la dimensionalidad se refiere a las propiedades no intuitivas de los datos observados cuando se trabaja en un espacio de alta dimensión*, específicamente relacionadas con la usabilidad y la interpretación de distancias y volúmenes. Este es uno de mis temas favoritos en Aprendizaje automático y estadísticas, ya que tiene amplias aplicaciones (no específicas de ningún método de aprendizaje automático), es muy contrario a la intuición y, por lo tanto, impresionante, tiene una aplicación profunda para cualquiera de las técnicas de análisis y ¡Tiene un nombre aterrador 'genial' como una maldición egipcia!
Para una comprensión rápida, considere este ejemplo: Digamos que dejó caer una moneda en una línea de 100 metros. ¿Cómo lo encuentras? Simple, simplemente camine sobre la línea y busque. Pero, ¿y si es de 100 x 100 m2? ¿campo? Ya se está poniendo difícil tratar de buscar en un campo de fútbol (más o menos) una sola moneda. Pero, ¿y si es un espacio de 100 x 100 x 100 m3? Ya sabes, el campo de fútbol ahora tiene treinta pisos de altura. ¡Buena suerte encontrando una moneda allí! Eso, en esencia, es "maldición de la dimensionalidad".
Muchos métodos de ML usan Medida de distancia
La mayoría de los métodos de segmentación y agrupación se basan en el cálculo de distancias entre observaciones. La conocida segmentación k-Means asigna puntos al centro más cercano . DBSCAN y el agrupamiento jerárquico también requerían métricas de distancia. Los algoritmos de detección de valores atípicos basados en la distribución y la densidad también hacen uso de la distancia relativa a otras distancias para marcar los valores atípicos.
Las soluciones de clasificación supervisada como el método k-Nearest Neighbors también usan la distancia entre las observaciones para asignar clases a las observaciones desconocidas. El método Support Vector Machine implica transformar las observaciones en torno a Kernels seleccionados en función de la distancia entre la observación y el kernel.
La forma común de los sistemas de recomendación implica la similitud basada en la distancia entre los vectores de atributos del usuario y del elemento. Incluso cuando se utilizan otras formas de distancias, el número de dimensiones juega un papel en el diseño analítico.
Una de las métricas de distancia más comunes es la métrica de distancia euclidiana, que es simplemente la distancia lineal entre dos puntos en un hiperespacio multidimensional. La distancia euclidiana para el punto i y el punto j en un espacio dimensional n se puede calcular como:
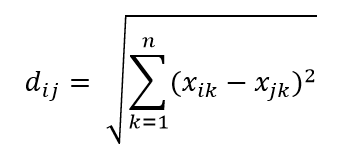
La distancia hace estragos en alta dimensión
Considere un proceso simple de muestreo de datos. Suponga que el cuadro exterior negro en la Fig. 1 es un universo de datos con una distribución uniforme de puntos de datos en todo el volumen, y que queremos muestrear el 1% de las observaciones encerradas en el cuadro interior rojo. La caja negra es un hipercubo en un espacio multidimensional en el que cada lado representa un rango de valor en esa dimensión. Para un ejemplo tridimensional simple en la Fig. 1, podemos tener el siguiente rango:
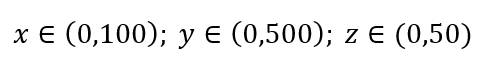
Figura 1: Muestreo
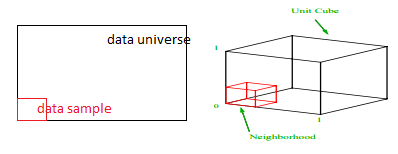
¿Cuál es la proporción de cada rango que debemos muestrear para obtener esa muestra del 1%? Para 2 dimensiones, el 10 % del rango logrará un muestreo general del 1 %, por lo que podemos seleccionar x∈(0,10) e y∈(0,50) y esperar capturar el 1 % de todas las observaciones. Esto se debe a que 10%2=1%. ¿Espera que esta proporción sea mayor o menor para las 3 dimensiones?
A pesar de que nuestra búsqueda ahora va en otra dirección, la proporción en realidad aumenta al 21,5 %. Y no solo aumenta, por solo una dimensión adicional, ¡se duplica! ¡Y puede ver que tenemos que cubrir casi una quinta parte de cada dimensión solo para obtener una centésima parte del total! En 10 dimensiones, esta proporción es del 63 % y en 100 dimensiones, que no es un número poco común de dimensiones en cualquier aprendizaje automático de la vida real, ¡uno tiene que muestrear el 95 % del rango a lo largo de cada dimensión para muestrear el 1 % de las observaciones! Este resultado alucinante se debe a que, en dimensiones altas, la dispersión de los puntos de datos se vuelve más grande incluso si se distribuyen uniformemente.

Esto tiene consecuencias en términos de diseño de experimentos y muestreo. El proceso se vuelve muy costoso desde el punto de vista computacional, incluso en la medida en que el muestreo se aproxima asintóticamente a la población a pesar de que el tamaño de la muestra sigue siendo mucho más pequeño que la población.
Considere otra gran consecuencia de la alta dimensionalidad. Muchos algoritmos miden la distancia entre dos puntos de datos para definir algún tipo de cercanía (DBSCAN, Kernels, k-Nearest Neighbor) en referencia a algún umbral de distancia predefinido. En 2 dimensiones, podemos imaginar que dos puntos están cerca si uno cae dentro de cierto radio de otro. Considere la imagen de la izquierda en la Fig. 2. ¿Cuál es la proporción de puntos uniformemente espaciados dentro del cuadrado negro que cae dentro del círculo rojo? eso es sobre
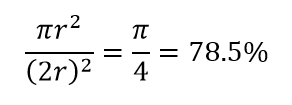
Figura 2: Cercanía
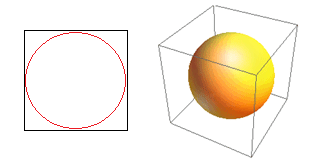
Entonces, si coloca el círculo más grande posible dentro del cuadrado, cubre el 78% del cuadrado. Sin embargo, la esfera más grande posible dentro del cubo cubre solo
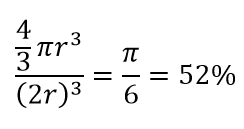
del volumen ¡Este volumen se reduce exponencialmente a 0.24% para solo 10 dimensiones! Lo que significa esencialmente que en el mundo de alta dimensión, cada punto de datos está en las esquinas y nada es realmente el centro del volumen, o en otras palabras, ¡el volumen central se reduce a nada porque (casi) no hay centro! Esto tiene enormes consecuencias para los algoritmos de agrupamiento basados en la distancia. ¡Todas las distancias comienzan a verse iguales y cualquier distancia mayor o menor que otra es una fluctuación aleatoria en los datos en lugar de una medida de disimilitud!
La Fig. 3 muestra datos 2D generados aleatoriamente y las correspondientes distancias de todos a todos. El coeficiente de variación de la distancia, calculado como la desviación estándar dividida por la media, es del 45,9 %. El número correspondiente de datos 5-D generados de manera similar es 26,5% y para 10-D es 19,1%. Es cierto que esta es una muestra, pero la tendencia respalda la conclusión de que en dimensiones altas cada distancia es aproximadamente la misma, ¡y ninguna está cerca o lejos!
Figura 3: Agrupación de distancia
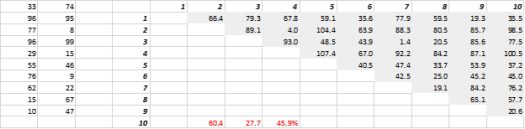
La alta dimensión también afecta a otras cosas
Aparte de las distancias y los volúmenes, el número de dimensiones crea otros problemas prácticos. Los requisitos de memoria del sistema y tiempo de ejecución de la solución a menudo aumentan de forma no lineal con el aumento del número de dimensiones. Debido al aumento exponencial de las soluciones factibles, muchos métodos de optimización no pueden alcanzar los óptimos globales y tienen que arreglárselas con los óptimos locales. Además, en lugar de una solución de forma cerrada, la optimización debe utilizar algoritmos basados en la búsqueda, como el descenso de gradiente, el algoritmo genético y el recocido simulado. Más dimensiones introducen la posibilidad de correlación y la estimación de parámetros puede resultar difícil en los enfoques de regresión.
Tratar con alta dimensión
Esta será una publicación de blog separada en sí misma, pero el análisis de correlación, la agrupación, el valor de la información, el factor de inflación de la varianza, el análisis de componentes principales son algunas de las formas en que se puede reducir el número de dimensiones.
* El número de variables, observaciones o características de las que se compone un punto de datos se denomina dimensión de los datos. Por ejemplo, cualquier punto en el espacio se puede representar usando 3 coordenadas de largo, ancho y alto, y tiene 3 dimensiones
