Estimación de densidad usando histogramas

Las funciones de densidad de probabilidad (PDF) describen la probabilidad de observar alguna variable aleatoria continua en alguna región del espacio. Para una variable aleatoria unidimensional X, recuerde que la PDF f(x) sigue las propiedades que

Probabilidad de que la variable tome valores entre

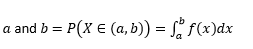
probabilidad de que la variable tome valores exactamente iguales a

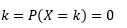
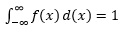
La estimación de dicho PDF a partir de una muestra de observaciones es un problema común en el aprendizaje automático. Esto es útil en muchos algoritmos de detección de valores atípicos en los que buscamos estimar la distribución "verdadera" en función de las observaciones de muestra y luego clasificar algunas de las observaciones existentes o nuevas como atípicos o no. Por ejemplo, una aseguradora de automóviles interesada en detectar un fraude podría examinar la solicitud de monto de reclamo para cada tipo de trabajo de carrocería, por ejemplo, reemplazo de parachoques, y marcar para posible fraude cualquier monto que sea demasiado alto. A modo de otro ejemplo, un psicólogo infantil puede examinar el tiempo necesario para completar una tarea determinada en diferentes niños y marcar a los niños que tardan demasiado o demasiado poco tiempo para una posible investigación.

En esta publicación de blog, discutimos cómo podemos aprender el PDF de una muestra de observaciones , para que podamos calcular la probabilidad de cada observación y decidir si es una ocurrencia común o rara.

Estimación de densidad usando histograma

Primero generamos algunos datos aleatorios para demostración.

set.seed(123)
data <- c(rnorm(200, 10, 20), rnorm(200, 60, 30), runif(200, 120, 180)) # 600 points

A continuación, los visualizamos para nuestra comprensión, usando histograma, como en la Figura 1.

# Plot 1
hist(data, breaks=50, freq=F, main="Univariate Distribution", xlab="Data Value")
# Plot 2
hist(data, breaks=20, freq=F, main="", xlab="20 Data Bins", col='red', border='red')
par(new=T)
hist(data, breaks=100, freq=F, main="Univariate Distribution", xlab=NULL, xaxt='n', yaxt='n')

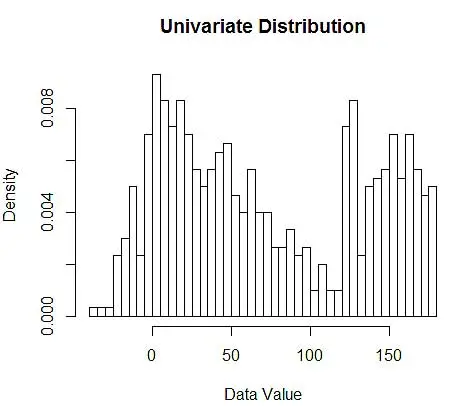
Si bien los histogramas son gráficos para la visualización de datos, también puede ver que son nuestra primera estimación de la densidad. Más específicamente, podemos estimar la densidad dividiendo los datos en contenedores y asumiendo que la densidad es constante dentro de ese rango de contenedores y tiene un valor igual al número de observaciones que caen en ese contenedor como proporción del número total de observaciones.

Por lo tanto, el PDF estimado es

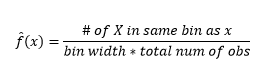
Y se da cuenta de que ha hecho una suposición sobre el ancho del contenedor que afectará la estimación de la densidad. Por lo tanto , bin-width es un parámetro para el modelo de estimación de densidad usando histograma . Sin embargo, el hecho pasado por alto es que también estamos trabajando con un parámetro más, que es la posición inicial del primer contenedor . Puede ver cómo eso puede afectar las estimaciones de densidad para todos los contenedores. Para ver el impacto del ancho del contenedor, la Figura 2 superpone estimaciones de densidad con histogramas de 20 y 100 contenedores. Mire la región rodeada, donde menos recipientes/más gruesos dan una estimación de densidad plana, mientras que muchos recipientes/más finos dan una estimación de densidad variable. Para el punto amarillo, las estimaciones de densidad oscilarán entre 0,004 y 0,008 a partir de dos modelos diferentes.

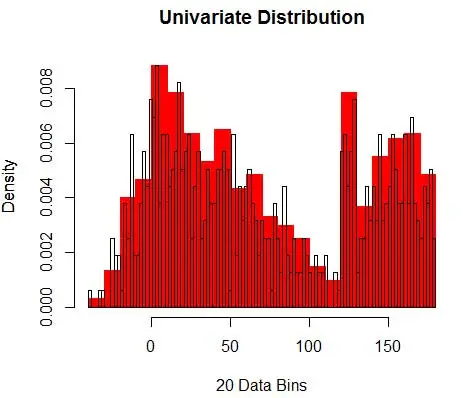
Por lo tanto, la selección correcta de los parámetros es crucial para obtener la estimación correcta de la densidad. Llegaremos a eso, pero tenga en cuenta que también hay otros problemas con los histogramas. Las estimaciones de densidad que utilizan histogramas son bastante desiguales y discontinuas . La densidad es plana para un contenedor y luego, de repente, cambia drásticamente para un punto infinitesimalmente fuera del contenedor. Esto hace que la consecuencia de una estimación incorrecta sea aún peor para los problemas prácticos.

Por último, hemos estado trabajando con variables de una sola dimensión para facilitar la ilustración, pero en la práctica la mayoría de los problemas son multidimensionales. Dado que la cantidad de contenedores crece exponencialmente con la cantidad de dimensiones, la cantidad de observaciones requeridas para estimar la densidad también crece . De hecho, es plausible que, a pesar de tener millones de observaciones, muchos contenedores permanezcan vacíos o contengan observaciones de un solo dígito. Con solo 50 contenedores cada uno en solo 3 dimensiones, tenemos 503 = 125 000 celdas que deben llenarse. Eso viene en promedio de 8 observaciones por celda, suponiendo una distribución uniforme, un millón de datos de entrenamiento de observación.

¿Cómo seleccionar los parámetros correctos?

Para bin-ancho n número de observaciones N para bin J proporción de observaciones es

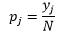
y la densidad estimada es

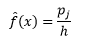
La teoría estadística demuestra que mientras f(x) es el valor esperado de la densidad en el contenedor, la varianza de la densidad es

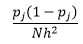
Si bien podemos obtener una mejor estimación de la densidad al reducir el ancho del contenedor n , aumentamos la varianza de la estimación, ya que intuitivamente podemos sentir que el ancho del contenedor es demasiado fino. Podemos utilizar la técnica de validación cruzada dejar uno fuera para estimar el conjunto óptimo de parámetros. Podemos estimar la densidad usando todas las observaciones menos una, y luego calcular la densidad de esa observación omitida y medir el error en la estimación. Resolver esto matemáticamente para histogramas da una solución de forma cerrada para la función de pérdida para un ancho de contenedor dado.

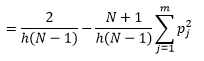
donde m es el número de contenedores. Los detalles técnicos de lo anterior se encuentran en esta conferencia [pdf] . Podemos trazar esta función de pérdida para varios números de contenedores (Figura 3)

getLoss <- function(n.break) {
N <- 600
res <- hist(data, breaks=n.break, freq=F)
bin <- as.numeric(res$breaks)
h <- bin[2]-bin[1]
p <- res$density
p <- p * h
return ( 2/(h*(N-1)) - ( (N+1)/(h*(N-1))*sum(p*p) ) )
}
loss.func <- data.frame(n=1:600)
loss.func$J <- sapply(loss.func$n, function(x) getLoss(x))
# Plot 3
plot(loss.func$n, loss.func$J, col='red', type='l')
opt.break <- max(loss.func[loss.func$J == min(loss.func$J), 'n'])
print(opt.break)
# Plot 4
hist(data, breaks=opt.break, freq=F, main="Univariate Distribution", xlab="15 Data Bins")

y obtenga el número óptimo como 15. En realidad, cualquier cosa entre 8 y 15 está bien.

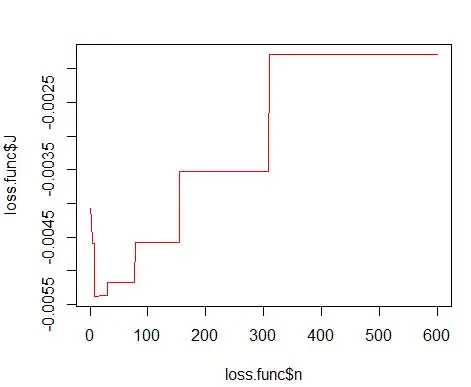
En consecuencia, debajo de la Figura 4 se encuentra la estimación de densidad que equilibra los valores de densidad y la granularidad (con una compensación óptima de sesgo y varianza).

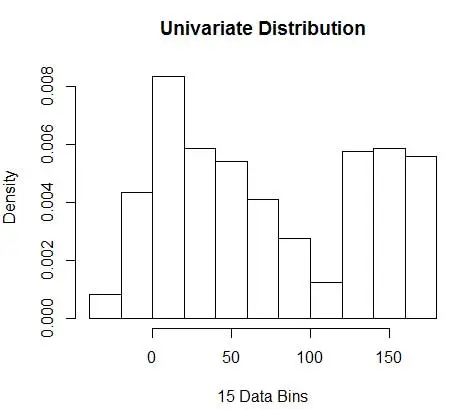
Si te sientes un poco incómodo en este punto, entonces estoy contigo. Aunque el número de contenedores es matemáticamente óptimo, parece una estimación demasiado aproximada. No hay un sentimiento intuitivo de por qué hemos hecho el mejor trabajo. Y sin olvidar otras preocupaciones sobre la posición inicial, la estimación discontinua y la maldición de la dimensionalidad. No te desesperes, hay una mejor manera. En la próxima publicación hablaremos sobre la Estimación de Densidad usando Kernels.