Medición de la distancia en el hiperespacio

Cualquiera que esté ligeramente familiarizado con las técnicas analíticas habría notado muchos algoritmos que se basan en distancias entre puntos de datos para su aplicación. Cada observación, o instancia de datos, generalmente se representa como un vector multidimensional, y la entrada al algoritmo requiere distancias entre cada par de tales observaciones.

El método de cálculo de la distancia depende del tipo de datos: numéricos, categóricos o mixtos. Algunos de los algoritmos se aplican a una sola clase de observaciones, mientras que otros funcionan en múltiples. En esta publicación, discutiremos las medidas de distancia que funcionan con datos numéricos. Quizás hay más formas en que se puede medir la distancia en el hiperespacio multidimensional de las que se pueden cubrir en una sola publicación de blog, y siempre se pueden inventar nuevas formas, pero analizamos algunas de las métricas de distancia comunes y sus méritos relativos.

Para el propósito del resto de la publicación del blog, implicamos

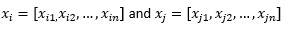
para referirse a dos observaciones o vectores de datos.

Primero prepara los datos...

Antes de revisar diferentes métricas de distancia, debemos preparar los datos:

Transformación a vector numérico

Para la observación mixta, que contiene dimensiones tanto numéricas como categóricas, el primer paso es transformar realmente la dimensión categórica en dimensión(es) numérica(s). Una dimensión categórica con tres valores potenciales se puede convertir en dos o tres dimensiones numéricas con valores binarios. Dado que esta variable categórica toma necesariamente uno de tres valores, una de las tres dimensiones numéricas estará perfectamente correlacionada con las otras dos. Esto puede o no estar bien dependiendo de su aplicación.

Si la observación es puramente categórica, como una cadena de texto (oraciones de longitud variable) o una secuencia del genoma (secuencias de longitud fija), entonces se puede aplicar directamente alguna métrica de distancia especial sin transformar los datos en formato numérico. Discutiremos estos algoritmos en la próxima publicación.

Normalización

Dependiendo de su caso de uso, es posible que desee normalizar cada dimensión en la misma escala, de modo que la distancia a lo largo de cualquier dimensión no influya indebidamente en la distancia total entre las observaciones. Lo mismo se discutió en el algoritmo k-Means. Hay dos tipos de normalización posibles:

La normalización de rango (reescalado) normaliza los datos para que estén en el rango 0-1, restando el valor mínimo de cada dimensión y luego dividiéndolos por el rango de valores en esa dimensión.

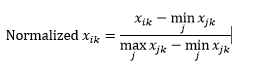
El primer problema con la normalización del rango es que un valor invisible puede normalizarse más allá del rango 0-1. Sin embargo, esto generalmente no es una preocupación para la mayoría de las métricas de distancia, pero si el algoritmo no puede manejar valores negativos, entonces esto puede ser un problema. El segundo problema es que esto depende en gran medida de los valores atípicos. Si una observación tiene un valor muy extremo (alto o bajo) para una dimensión, el valor normalizado de esa dimensión para otras observaciones se agrupará y perderá sus poderes de discriminación.

La normalización estándar (escala z) normaliza la dimensión para que tenga una media de 0 y una desviación estándar, restando la media de esa dimensión de cada observación y luego dividiéndola por la desviación estándar del valor de esa dimensión en todas las observaciones.

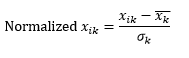
Esto generalmente mantiene los datos en un rango de -5 a +5, aproximadamente, y evita la influencia de un valor extremo.

Hemos simulado la escala z de dos observaciones. Simulado, porque realmente necesitamos muchas más que dos observaciones para calcular la media y la desviación estándar de cada dimensión, y aquí hemos asumido estos dos números para cada dimensión.

Luego calcula la distancia...

La distancia euclidiana , también conocida como distancia "a vuelo de pájaro", es la distancia más corta en el hiperespacio multidimensional entre dos puntos. Está familiarizado con esto en el plano 2D o en el espacio 3D (esto es una línea), pero un concepto similar se extiende a dimensiones más altas. La distancia euclidiana entre vectores en el espacio n-dimensional se calcula como

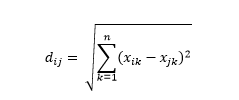
Para ejemplos de vectores de datos transformados, esto es

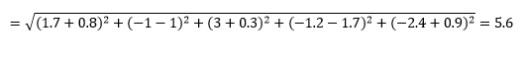
Esta es la métrica más común y, a menudo, muy adecuada para la mayoría de las aplicaciones. Una variante de esto es la distancia euclidiana al cuadrado, que es solo la suma de las diferencias al cuadrado.

La distancia de Manhattan , llamada así por la estructura de cuadrícula Este-Oeste-Norte-Sur de las calles de Manhattan en Nueva York, es la distancia entre dos puntos cuando se cruzan en paralelo a los ejes.

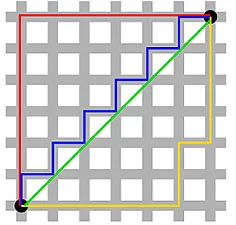
Distancia de Manhattan
Distancia euclidiana

Esto se calcula como

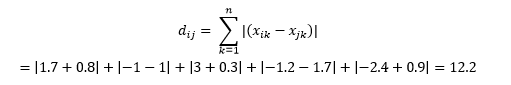
Esto puede ser útil en alguna aplicación donde la distancia se usa en un sentido físico real en lugar del sentido de "disemejanza" del aprendizaje automático. Por ejemplo, si necesita calcular la distancia recorrida por un camión de bomberos para llegar a un punto, usar esto es más práctico.

La distancia de Canberra es una variante ponderada de la distancia de Manhattan y se calcula como

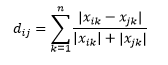
La distancia L-norma es una extensión de las dos anteriores, o puede decir que las dos anteriores son casos específicos de distancia L-norma, y ​​se define como

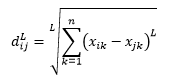
donde L es un entero positivo. No he encontrado ningún caso en el que necesite usar esto, pero aún es bueno conocer esta posibilidad. Por ejemplo, la distancia de 3 normas será

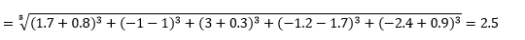
Tenga en cuenta que L generalmente debe ser un número entero par, ya que no queremos que las contribuciones de distancia positivas o negativas se cancelen.

La distancia de Minkowski es una generalización de la distancia L-norma, donde L podría tomar cualquier valor desde 0 hasta incluir valores fraccionarios. La distancia de Minkowski de orden p se define como

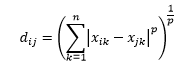
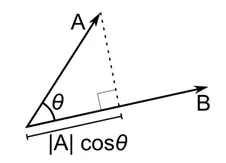
La distancia del coseno es la medida del ángulo entre dos vectores, cada uno de los cuales representa dos observaciones, y se forma al unir el punto de datos con el origen. La distancia del coseno varía de 0 (exactamente igual) a 1 (sin conexión), y se calcula como

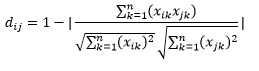
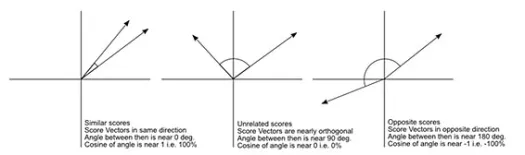
Si bien esta es una medida de distancia más común cuando se trabaja con datos categóricos, también se puede definir para un vector numérico. Para nuestros vectores numéricos, esto será

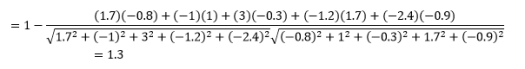
Pero cuidado con las advertencias…

Sabías que esto vendría, ¿no? Si el análisis fuera solo un montón de fórmulas matemáticas, no necesitaremos gente inteligente como usted para hacerlo.

Lo primero a tener en cuenta es que las distancias calculadas por diferentes métricas son diferentes. Puede sentirse tentado a pensar que la distancia del coseno de 1.3 es la más pequeña y, por lo tanto, indica que los vectores son los más cercanos, pero esta no es la forma correcta de interpretar. Las distancias entre diferentes métodos no se pueden comparar, y solo se pueden comparar las distancias entre diferentes pares de observaciones bajo el mismo método. Las distancias tienen un significado relativo y no un significado absoluto por sí mismas .

Esto lleva a la siguiente pregunta sobre cómo seleccionar la métrica de distancia correcta. Desafortunadamente, no hay una respuesta verdadera. Según el tipo de datos, el contexto, el problema comercial, la aplicación y el método de entrenamiento del modelo, diferentes métricas dan resultados diferentes. Tendrá que usar el juicio, hacer suposiciones o probar el rendimiento del modelo para decidir cuál es la métrica correcta .

La segunda advertencia es la que a menudo repito sobre la maldición de la dimensionalidad. En dimensiones más altas, las distancias no se comportan de la manera que intuitivamente pensamos que lo hacen , y el analista debe ser extremadamente cauteloso al usar cualquier métrica.

La tercera advertencia es sobre la relación entre las distancias entre tres observaciones. Algunas métricas admiten la desigualdad triangular y otras no . La desigualdad triangular implica que siempre es más corto ir del punto i al punto j directamente, en lugar de pasar por cualquier punto intermedio k. Matemáticamente,

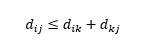
Dependiendo de su aplicación, esto puede o no ser una propiedad requerida de la métrica de distancia.

Oh, una cosa más, "distancia" es lo opuesto a "similitud". A mayor distancia, menor similitud y viceversa. Los algoritmos de agrupamiento funcionan en distancias y los algoritmos de recomendación funcionan en similitud, pero esencialmente están hablando de lo mismo.

Entonces, ¿cómo puedes transformar el número de distancia en número de similitud?