Malédiction de dimensionnalité
Publié: 2015-07-08Qu'est-ce que la malédiction de la dimensionnalité
La malédiction de la dimensionnalité fait référence aux propriétés non intuitives des données observées lors du travail dans un espace de grande dimension*, spécifiquement liées à la convivialité et à l'interprétation des distances et des volumes. C'est l'un de mes sujets préférés dans l'apprentissage automatique et les statistiques car il a de larges applications (non spécifiques à une méthode d'apprentissage automatique), il est très contre-intuitif et donc impressionnant, il a une application profonde pour toutes les techniques d'analyse, et il a un nom effrayant "cool" comme une malédiction égyptienne !
Pour une compréhension rapide, considérez cet exemple : Disons que vous avez laissé tomber une pièce sur une ligne de 100 mètres. Comment tu le trouves? Simple, il suffit de marcher sur la ligne et de chercher. Mais que se passe-t-il si c'est 100 x 100 m². champ? Il devient déjà difficile d'essayer de rechercher (à peu près) un terrain de football pour une seule pièce. Mais que se passe-t-il si c'est un espace de 100 x 100 x 100 m3 ? ! Vous savez, le terrain de football a maintenant une hauteur de trente étages. Bonne chance pour trouver une pièce là-bas ! C'est essentiellement la "malédiction de la dimensionnalité".
De nombreuses méthodes ML utilisent la mesure de distance
La plupart des méthodes de segmentation et de regroupement reposent sur le calcul des distances entre les observations. La segmentation k-Means bien connue attribue des points au centre le plus proche . DBSCAN et le clustering hiérarchique nécessitaient également des métriques de distance. Les algorithmes de détection des valeurs aberrantes basés sur la distribution et la densité utilisent également la distance par rapport à d'autres distances pour marquer les valeurs aberrantes.
Les solutions de classification supervisée comme la méthode k-Nearest Neighbors utilisent également la distance entre les observations pour attribuer une classe à une observation inconnue. La méthode Support Vector Machine consiste à transformer les observations autour de noyaux sélectionnés en fonction de la distance entre l'observation et le noyau.
Une forme courante de systèmes de recommandation implique une similarité basée sur la distance entre les vecteurs d'attributs d'utilisateur et d'élément. Même lorsque d'autres formes de distances sont utilisées, le nombre de dimensions joue un rôle dans la conception analytique.
L'une des métriques de distance les plus courantes est la métrique de distance euclidienne, qui est simplement une distance linéaire entre deux points dans un hyper-espace multidimensionnel. La distance euclidienne pour le point i et le point j dans un espace à n dimensions peut être calculée comme suit :
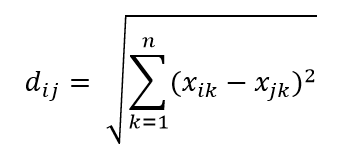
La distance fait des ravages en haute dimension
Envisagez un processus simple d'échantillonnage des données. Supposons que la boîte extérieure noire de la figure 1 soit un univers de données avec une distribution uniforme des points de données sur tout le volume, et que nous voulions échantillonner 1 % des observations entourées d'une boîte intérieure rouge. La boîte noire est un hyper-cube dans un espace multidimensionnel, chaque côté représentant une plage de valeurs dans cette dimension. Pour un exemple tridimensionnel simple sur la figure 1, nous pouvons avoir la plage suivante :
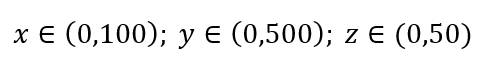
Figure 1 : Échantillonnage
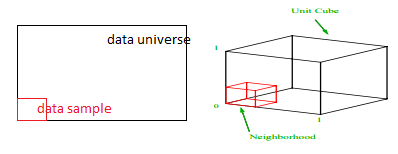
Quelle est la proportion de chaque plage devrions-nous échantillonner pour obtenir cet échantillon de 1 % ? Pour 2 dimensions, 10 % de la plage permettront d'obtenir un échantillonnage global de 1 %, nous pouvons donc sélectionner x∈(0,10) et y∈(0,50) et nous attendre à capturer 1 % de toutes les observations. C'est parce que 10%2=1%. Vous attendez-vous à ce que cette proportion soit supérieure ou inférieure pour la 3D ?
Même si notre recherche va maintenant dans une autre direction, la proportionnalité augmente en fait à 21,5 %. Et non seulement augmente, pour une seule dimension supplémentaire, il double ! Et vous pouvez voir que nous devons couvrir presque un cinquième de chaque dimension pour obtenir un centième de l'ensemble ! En 10 dimensions, cette proportion est de 63 % et en 100 dimensions - ce qui n'est pas un nombre rare de dimensions dans tout apprentissage automatique réel - il faut échantillonner 95 % de la plage le long de chaque dimension pour échantillonner 1 % des observations ! Ce résultat époustouflant se produit parce que dans les dimensions élevées, la propagation des points de données devient plus grande même s'ils sont uniformément répartis.

Cela a des conséquences en termes de conception de l'expérience et d'échantillonnage. Le processus devient très coûteux en calcul, même dans la mesure où l'échantillonnage se rapproche asymptotiquement de la population malgré la taille de l'échantillon qui reste beaucoup plus petite que la population.
Considérez une autre conséquence énorme de la haute dimensionnalité. De nombreux algorithmes mesurent la distance entre deux points de données pour définir une sorte de proximité (DBSCAN, Kernels, k-Nearest Neighbour) en référence à un seuil de distance prédéfini. En 2 dimensions, on peut imaginer que deux points sont proches si l'un tombe dans un certain rayon d'un autre. Considérez l'image de gauche sur la Fig. 2. Quelle est la part des points uniformément espacés dans le carré noir à l'intérieur du cercle rouge ? C'est à peu près
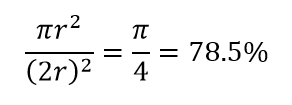
Figure 2 : Proximité
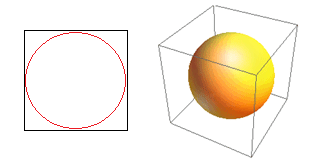
Donc, si vous placez le plus grand cercle possible à l'intérieur du carré, vous couvrez 78 % du carré. Pourtant, la plus grande sphère possible à l'intérieur du cube ne couvre que
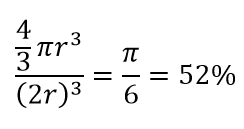
du volume. Ce volume se réduit de manière exponentielle à 0,24 % pour seulement 10 dimensions ! Ce que cela signifie essentiellement que dans un monde de haute dimension, chaque point de données se trouve dans les coins et rien n'est vraiment le centre du volume, ou en d'autres termes, le volume central se réduit à rien car il n'y a (presque) pas de centre ! Cela a d'énormes conséquences sur les algorithmes de clustering basés sur la distance. Toutes les distances commencent à se ressembler et toute distance plus ou moins que les autres est plus une fluctuation aléatoire des données plutôt qu'une mesure de dissemblance !
La figure 3 montre des données 2D générées de manière aléatoire et les distances tout-à-tout correspondantes. Le coefficient de variation de la distance, calculé comme l'écart type divisé par la moyenne, est de 45,9 %. Le nombre correspondant de données 5-D générées de manière similaire est de 26,5 % et de 19,1 % pour le 10-D. Certes, il s'agit d'un échantillon, mais la tendance soutient la conclusion qu'en haute dimension, chaque distance est à peu près la même, et aucune n'est proche ou éloignée !
Figure 3 : Regroupement des distances
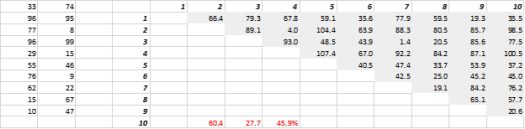
La haute dimension affecte également d'autres choses
Outre les distances et les volumes, le nombre de dimensions crée d'autres problèmes pratiques. Les exigences d'exécution de la solution et de mémoire système augmentent souvent de manière non linéaire avec l'augmentation du nombre de dimensions. En raison de l'augmentation exponentielle des solutions réalisables, de nombreuses méthodes d'optimisation ne peuvent pas atteindre les optima globaux et doivent se contenter des optima locaux. De plus, au lieu d'une solution de forme fermée, l'optimisation doit utiliser des algorithmes basés sur la recherche tels que la descente de gradient, l'algorithme génétique et le recuit simulé. Plus de dimensions introduisent une possibilité de corrélation et l'estimation des paramètres peut devenir difficile dans les approches de régression.
Faire face à la grande dimension
Ce sera un article de blog distinct en soi, mais l'analyse de corrélation, le regroupement, la valeur de l'information, le facteur d'inflation de la variance, l'analyse en composantes principales sont quelques-unes des façons dont le nombre de dimensions peut être réduit.
* Le nombre de variables, d'observations ou de caractéristiques d'un point de données est appelé dimension des données. Par exemple, n'importe quel point dans l'espace peut être représenté en utilisant 3 coordonnées de longueur, largeur et hauteur, et a 3 dimensions
