Estimation de la densité à l'aide d'histogrammes

Les fonctions de densité de probabilité (PDF) décrivent la probabilité d'observer une variable aléatoire continue dans une région de l'espace. Pour une variable aléatoire unidimensionnelle X, rappelez-vous que PDF f(x) suit les propriétés qui

Probabilité que la variable prenne des valeurs entre

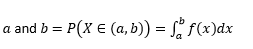
Probabilité que la variable prenne des valeurs exactement égales à

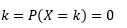
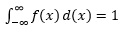
L'estimation d'un tel PDF à partir d'un échantillon d'observations est un problème courant dans l'apprentissage automatique. Cela est pratique dans de nombreux algorithmes de détection de valeurs aberrantes où nous cherchons à estimer la distribution "vraie" sur la base d'observations d'échantillons, puis à classer certaines des observations existantes ou nouvelles comme aberrantes ou non. Par exemple, un assureur automobile intéressé à attraper la fraude pourrait examiner la demande de montant de réclamation pour chaque type de carrosserie, par exemple, le remplacement du pare-chocs, et marquer comme fraude potentielle tout montant trop élevé. À titre d'autre exemple, un psychologue pour enfants peut examiner le temps nécessaire pour accomplir une tâche donnée chez différents enfants et marquer les enfants qui prennent trop de temps ou trop peu de temps pour une enquête potentielle.

Dans cet article de blog, nous expliquons comment apprendre le PDF à partir d'un échantillon d'observations , afin de pouvoir calculer la probabilité de chaque observation et décider s'il s'agit d'un événement courant ou rare.

Estimation de la densité à l'aide de l'histogramme

Nous générons d'abord des données aléatoires pour la démonstration.

set.seed(123)
data <- c(rnorm(200, 10, 20), rnorm(200, 60, 30), runif(200, 120, 180)) # 600 points

Ensuite, nous les visualisons pour notre compréhension, en utilisant un histogramme, comme dans la figure 1.

# Plot 1
hist(data, breaks=50, freq=F, main="Univariate Distribution", xlab="Data Value")
# Plot 2
hist(data, breaks=20, freq=F, main="", xlab="20 Data Bins", col='red', border='red')
par(new=T)
hist(data, breaks=100, freq=F, main="Univariate Distribution", xlab=NULL, xaxt='n', yaxt='n')

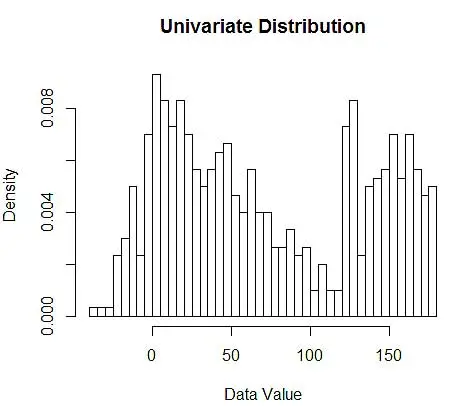
Alors que les histogrammes sont des graphiques pour la visualisation des données, vous pouvez également voir qu'ils sont notre première estimation de la densité. Plus précisément, nous pouvons estimer la densité en divisant les données en bacs et en supposant que la densité est constante dans cette plage de bacs et a une valeur égale au nombre d'observations tombant dans ce bac en proportion du nombre total d'observations.

Par conséquent, le PDF estimé est

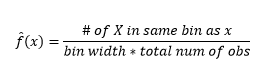
Et vous vous rendez compte que vous avez fait une hypothèse sur la largeur de bac qui aura un impact sur l'estimation de la densité. Par conséquent , bin-width est un paramètre du modèle d'estimation de la densité utilisant histogram . Cependant, un fait négligé est que nous travaillons également avec un autre paramètre - qui est la position de départ du premier bac . Vous pouvez voir comment cela peut affecter les estimations de densité pour tous les bacs. Pour voir l'impact de la largeur de bac, la figure 2 superpose les estimations de densité avec des histogrammes de 20 et 100 bacs. Regardez la région encerclée, où moins de bacs / plus grossiers donnent une estimation de densité plate, tandis que de nombreux bacs / plus fins donnent une estimation de densité variable. Pour le point jaune, les estimations de densité iront de 0,004 à 0,008 à partir de deux modèles différents.

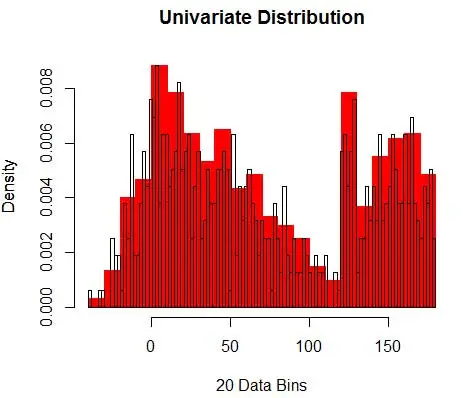
Ainsi, la sélection correcte des paramètres est cruciale pour obtenir la bonne estimation de la densité. Nous y reviendrons, mais notez qu'il existe également d'autres problèmes avec les histogrammes. Les estimations de densité à l'aide d'histogrammes sont assez saccadées et discontinues . La densité est plate pour un bac, puis change soudainement de manière drastique pour un point situé à l'infini à l'extérieur du bac. Cela rend les conséquences d'une mauvaise estimation encore pires pour les problèmes pratiques.

Enfin, nous avons travaillé avec une variable unidimensionnelle pour faciliter l'illustration, mais en pratique, la plupart des problèmes sont multidimensionnels. Étant donné que le nombre de bacs augmente de façon exponentielle avec le nombre de dimensions, le nombre d'observations nécessaires pour estimer la densité augmente également . En fait, il est plausible que malgré des millions d'observations, de nombreuses cases restent vides ou contiennent des observations à un seul chiffre. Avec seulement 50 bacs chacun en seulement 3 dimensions, nous avons 503 = 125 000 cellules qui doivent être remplies. Cela revient à une moyenne de 8 observations par cellule, en supposant une distribution uniforme, un million de données d'entraînement à l'observation.

Comment sélectionner les bons paramètres ?

Pour la largeur de classe n nombre d'observations N pour la classe J proportion d'observations est

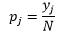
et l'estimation de la densité est

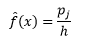
La théorie statistique prouve que si f (x) est la valeur attendue de la densité dans le bac, la variance de la densité est

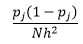
Bien que nous puissions obtenir une meilleure estimation de la densité en réduisant la largeur de bac n , nous augmentons la variance de l'estimation, car nous pouvons intuitivement ressentir une largeur de bac trop fine. Nous pouvons utiliser la technique de validation croisée sans sortie pour estimer l'ensemble optimal de paramètres. Nous pouvons estimer la densité en utilisant toutes les observations sauf une, puis calculer la densité de cette observation omise et mesurer l'erreur d'estimation. Résoudre cela mathématiquement pour les histogrammes donne une solution de forme fermée pour la fonction de perte pour une largeur de bac donnée.

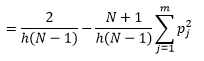
où m est le nombre de cases. Les détails techniques ci-dessus sont dans cette conférence [pdf] . Nous pouvons tracer cette fonction de perte pour différents nombres de bacs (Figure 3)

getLoss <- function(n.break) {
N <- 600
res <- hist(data, breaks=n.break, freq=F)
bin <- as.numeric(res$breaks)
h <- bin[2]-bin[1]
p <- res$density
p <- p * h
return ( 2/(h*(N-1)) - ( (N+1)/(h*(N-1))*sum(p*p) ) )
}
loss.func <- data.frame(n=1:600)
loss.func$J <- sapply(loss.func$n, function(x) getLoss(x))
# Plot 3
plot(loss.func$n, loss.func$J, col='red', type='l')
opt.break <- max(loss.func[loss.func$J == min(loss.func$J), 'n'])
print(opt.break)
# Plot 4
hist(data, breaks=opt.break, freq=F, main="Univariate Distribution", xlab="15 Data Bins")

et obtenez un nombre optimal de 15. En fait, tout ce qui se situe entre 8 et 15 convient.

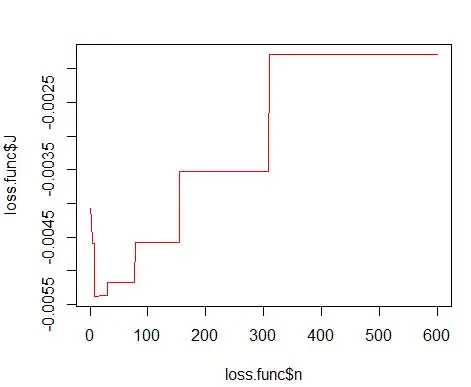
Par conséquent, sous la figure 4 se trouve l'estimation de la densité qui équilibre les valeurs de densité ainsi que la granularité (avec un compromis biais-variance optimal).

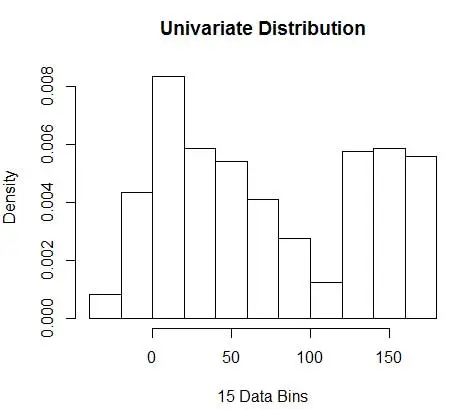
Si vous vous sentez un peu mal à l'aise à ce stade, je suis avec vous. Même si le nombre de bacs est mathématiquement optimal, cela semble être une estimation trop grossière. Il n'y a aucun sentiment intuitif pourquoi nous avons fait le meilleur travail. Et sans oublier d'autres préoccupations concernant la position de départ, l'estimation discontinue et la malédiction de la dimensionnalité. Ne désespérez pas, il existe un meilleur moyen. Dans le prochain article, nous parlerons de l'estimation de la densité à l'aide de noyaux.