Mesurer la distance dans l'hyperespace

Toute personne familiarisée avec les techniques analytiques aurait remarqué de nombreux algorithmes reposant sur les distances entre les points de données pour leur application. Chaque observation, ou instance de données, est généralement représentée sous forme de vecteur multidimensionnel, et l'entrée dans l'algorithme nécessite des distances entre chaque paire de ces observations.

La méthode de calcul de la distance dépend du type de données – numériques, catégorielles ou mixtes. Certains algorithmes s'appliquent à une seule classe d'observations, tandis que d'autres fonctionnent sur plusieurs. Dans cet article, nous discuterons des mesures de distance qui fonctionnent sur des données numériques. Il y a peut-être plus de façons de mesurer la distance dans l'hyperespace multidimensionnel que celles qui peuvent être couvertes dans un seul article de blog, et on peut toujours inventer de nouvelles façons, mais nous examinons certaines des mesures de distance courantes et leurs mérites relatifs.

Aux fins du reste de l'article de blog, nous sous-entendons

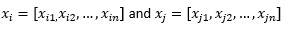
pour faire référence à deux observations ou vecteurs de données.

Préparez d’abord les données…

Avant d'examiner différentes mesures de distance, nous devons préparer les données :

Transformation en vecteur numérique

Pour l'observation mixte, qui contient à la fois des dimensions numériques et catégorielles, la première étape consiste à transformer réellement la dimension catégorique en dimension(s) numérique(s). Une dimension catégorielle avec trois valeurs potentielles peut être transformée en deux ou trois dimensions numériques avec des valeurs binaires. Puisque cette variable catégorielle prend nécessairement l'une des trois valeurs, l'une des trois dimensions numériques sera parfaitement corrélée avec les deux autres. Cela peut être correct ou non selon votre application.

Si l'observation est purement catégorique, telle qu'une chaîne de texte (phrases de longueur variable) ou une séquence du génome (séquences de longueur fixe), une métrique de distance spéciale peut être appliquée directement sans transformer les données en format numérique. Nous discuterons de ces algorithmes dans le prochain article.

Normalisation

En fonction de votre cas d'utilisation, vous souhaiterez peut-être normaliser chaque dimension sur la même échelle, afin que la distance le long d'une dimension n'influence pas indûment la distance globale entre les observations. La même chose a été discutée dans l'algorithme k-Means . Deux types de normalisation sont possibles :

La normalisation de plage (remise à l'échelle) normalise les données pour qu'elles soient dans la plage 0-1, en soustrayant la valeur minimale de chaque dimension, puis en divisant par la plage de valeurs dans cette dimension.

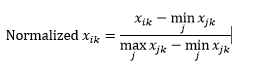
Le premier problème avec la normalisation de plage est qu'une valeur invisible peut être normalisée au-delà de la plage 0-1. Cependant, ce n'est généralement pas un problème pour la plupart des mesures de distance, mais si l'algorithme ne peut pas gérer les valeurs négatives, cela peut poser problème. Le deuxième problème est que cela dépend fortement des valeurs aberrantes. Si une observation a une valeur très extrême (élevée ou faible) pour une dimension, la valeur normalisée pour cette dimension pour les autres observations sera regroupée et perdra son pouvoir discriminant.

La normalisation standard (échelle z) normalise la dimension pour avoir 0 moyenne et 1 écart type, en soustrayant la moyenne de cette dimension de chaque observation, puis en divisant par l'écart type de la valeur de cette dimension sur toutes les observations.

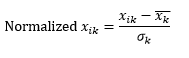
Cela conserve généralement les données dans une plage de -5 à +5, approximativement, et évite l'influence d'une valeur extrême.

Nous avons simulé la mise à l'échelle z de deux observations. Simulé, car nous avons vraiment besoin de beaucoup plus de deux observations pour calculer la moyenne et l'écart type de chaque dimension, et nous avons supposé ces deux nombres pour chaque dimension ici.

Calculez ensuite la distance...

La distance euclidienne - alias la distance "à vol d'oiseau" - est la distance la plus courte dans l'hyperespace multidimensionnel entre deux points. Vous êtes familier avec cela dans le plan 2D ou l'espace 3D (il s'agit d'une ligne), mais un concept similaire s'étend à des dimensions plus élevées. La distance euclidienne entre les vecteurs dans l'espace à n dimensions est calculée comme

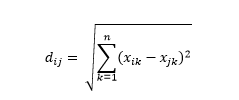
Pour les exemples de vecteurs de données transformés, il s'agit

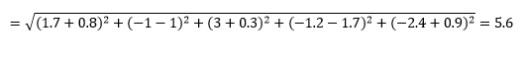
Il s'agit de la mesure la plus courante et souvent très adaptée à la plupart des applications. Une variante de ceci est la distance euclidienne au carré, qui est juste la somme des différences au carré.

La distance de Manhattan - nommée en raison de la grille Est-Ouest-Nord-Sud comme la structure des rues de Manhattan à New York - est la distance entre deux points lorsqu'ils traversent parallèlement aux axes.

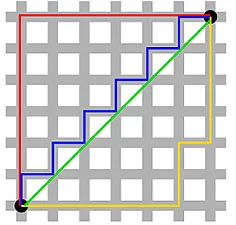
Manhattan Distance
Distance euclidienne

Ceci est calculé comme

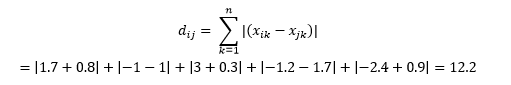
Cela peut être utile dans certaines applications où la distance est utilisée dans un sens réel et physique plutôt que dans un sens d'apprentissage automatique de "dissemblance". Par exemple, si vous avez besoin de calculer la distance parcourue par un camion de pompiers pour atteindre un point, il est alors plus pratique de l'utiliser.

La distance de Canberra est une variante pondérée de la distance de Manhattan, et est calculée comme

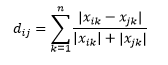
La distance de norme L est l'extension de plus de deux - ou vous pouvez dire qu'au-dessus de deux sont des cas spécifiques de distance de norme L - et est définie comme

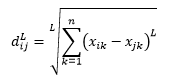
où L est un entier positif. Je n'ai rencontré aucun cas où j'avais besoin de l'utiliser, mais c'est toujours une bonne possibilité à savoir. Par exemple, la distance à la norme 3 sera

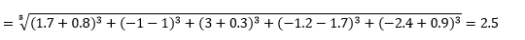
Notez que L devrait généralement être un entier pair puisque nous ne voulons pas que les contributions de distance positives ou négatives s'annulent.

La distance de Minkowski est une généralisation de la distance de norme L, où L peut prendre n'importe quelle valeur de 0 à des valeurs fractionnaires. La distance de Minkowski d'ordre p est définie comme

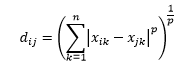
La distance cosinus est la mesure de l'angle entre deux vecteurs, chacun représentant deux observations, et formé en joignant le point de données à l'origine. La distance cosinus va de 0 (exactement identique) à 1 (pas de connexion) et est calculée comme suit

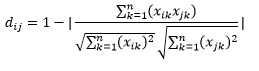
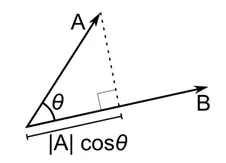
Bien qu'il s'agisse d'une mesure de distance plus courante lorsque vous travaillez avec des données catégorielles, cela peut également être défini pour un vecteur numérique. Pour nos vecteurs numériques, ce sera

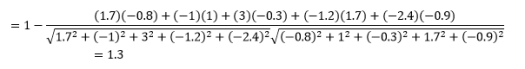
Mais attention aux mises en garde…

Vous saviez que ça allait arriver, n'est-ce pas ? Si l'analyse n'était qu'un tas de formules mathématiques, nous n'aurions pas besoin de gens intelligents comme vous pour le faire.

La première chose à noter est que les distances calculées par différentes métriques sont différentes. Vous pourriez être tenté de penser que la distance cosinus de 1,3 est la plus petite et indique donc que les vecteurs sont les plus proches, mais ce n'est pas la bonne façon d'interpréter. Les distances entre différentes méthodes ne peuvent pas être comparées, et seules les distances entre différentes paires d'observations sous la même méthode peuvent être comparées. Les distances ont une signification relative et non une signification absolue par elles-mêmes .

Cela conduit à la question suivante sur la façon de sélectionner la bonne mesure de distance. Malheureusement, il n'y a pas de vraie réponse. Selon le type de données, le contexte, le problème métier, l'application et la méthode de formation du modèle, différentes métriques donnent des résultats différents. Vous devrez faire preuve de jugement, formuler des hypothèses ou tester les performances du modèle pour décider de la bonne métrique .

La deuxième mise en garde est celle que j'ai souvent répétée à propos de la malédiction de la dimensionnalité. Dans les dimensions supérieures, les distances ne se comportent pas comme nous le pensons intuitivement , et l'analyste doit être extrêmement prudent lorsqu'il utilise une métrique.

La troisième mise en garde concerne la relation entre les distances entre trois observations. Certaines métriques prennent en charge l'inégalité triangulaire et d'autres non . L'inégalité triangulaire implique qu'il est toujours plus court d'aller du point i au point j directement, plutôt que via n'importe quel point intermédiaire k. Mathématiquement,

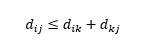
Selon votre application, cela peut ou non être une propriété requise de la métrique de distance.

Oh, encore une chose, "distance" est à l'opposé de "similitude". Plus la distance est élevée, plus la similarité est faible, et vice-versa. Les algorithmes de clustering fonctionnent sur les distances et les algorithmes de recommandation fonctionnent sur la similarité, mais ils parlent essentiellement de la même chose.

Alors, comment pouvez-vous transformer le nombre de distance en nombre de similarité ?