Utiliser les régressions Excel pour mieux comprendre les KPI
Publié: 2021-10-23Un groupe d'entre nous ici à Hanapin a récemment participé à un cours Excel gratuit de 21 jours dirigé par le célèbre expert Microsoft Excel, le Dr Wayne Winston. Le cours lui-même semblait lent au début, mais a finalement révélé plusieurs capacités Excel que je n'avais jamais connues. Le plus excitant d'entre eux, pour moi, est la capacité de régresser plusieurs variables sans un logiciel statistique avancé (tel que STATA). Dans cet article, je vais partager étape par étape pour configurer et exécuter des régressions dans Excel, et comment cet outil peut vous aider dans vos analyses PPC et votre gestion de compte.
Excusez-moi, je régresse
Avant de creuser dans la mise en œuvre technique, vous vous demandez peut-être : « Qu'est-ce qu'une régression dans le monde ? » En bref, les régressions examinent les relations entre les variables. Pour toute variable dépendante (« Y »), quel ensemble de variables indépendantes (« X ») contribue à la variation Y, et quelle part de ce comportement le modèle de régression explique-t-il ? (Voir ici pour un examen approfondi des analyses de régression)
Les régressions linéaires (ou régressions linéaires multiples) sont les plus courantes, s'insérant dans une équation sommée de la forme :
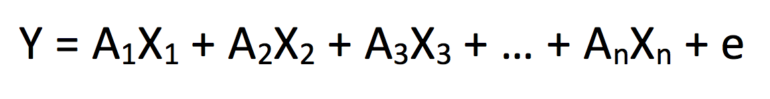
où Y est la variable dépendante, X 1 – X n représentent un ensemble de n variables indépendantes et A 1 – A n sont les constantes de coefficient correspondant à X 1 – X n . Il s'agit de la construction d'un modèle statistique de base, et nous reconnaissons donc qu'il y aura une certaine incohérence entre nos résultats prédits et observés pour chaque itération « y ». Ainsi, le terme d'erreur « + e » est ajouté pour tenir compte de cette variance.
Pourquoi régresser en PPC ?
Les régressions peuvent être utilisées dans n'importe quel nombre d'analyses. Par exemple, vous pouvez envisager l'effet des modifications d'enchères au CPC sur la valeur moy. Position, Taux d'impressions perdues ou Niveau de qualité. Vous pouvez examiner quel élément (CTR attendu, expérience de la page de destination ou pertinence de l'annonce) a le plus d'impact sur le niveau de qualité de votre compte, de votre campagne ou de vos mots clés. Comme nous le verrons dans l'exemple ci-dessous, vous souhaitez peut-être découvrir le rôle que jouent les CPC et les taux de conversion sur les Réseaux de Recherche et Display dans le CPA global de votre compte.
Quel que soit votre objectif final, le processus de configuration et de détermination de la valeur de votre modèle de régression est le même.
Étape 1 : préparez vos données
Comme pour toute analyse, un bon résultat nécessite des données de qualité qui ont été correctement préparées. Pour de bons résultats de régression, vous avez besoin d'une quantité suffisante de données (au moins autant de points de données que le nombre de variables indépendantes, mais plus vous disposez de données, plus votre modèle de régression peut être précis). Pour augmenter le nombre de points de données, vous pouvez envisager de segmenter vos données par jour, semaine ou mois (selon la période examinée).
Pour notre exemple, nous utilisons les données des 24 derniers mois dans Adwords. Après avoir téléchargé un rapport de campagne (segmenté par mois), nous créons un tableau croisé dynamique pour examiner les clics, les coûts et les conversions par mois et par type de campagne :
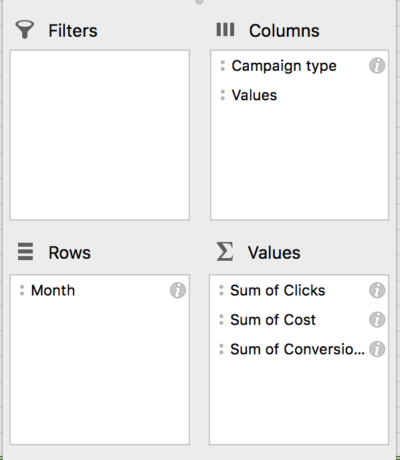
À partir de là, nous pouvons calculer le CPA, le CPC et le CVR pour chaque réseau, ainsi que le CPA total. Ensuite, il suffit d'un simple copier-coller des données dans une nouvelle feuille, nous sommes prêts à commencer à régresser !
Étape 2 : Construisez votre modèle (choix des variables)
La construction de modèles comporte deux éléments principaux : une planification réfléchie et une révision flexible. Une planification réfléchie consiste à déterminer quelles variables seraient logiquement les mieux adaptées à votre modèle (et quelles données sont disponibles pour une utilisation). Passer un peu plus de temps dans la phase de planification peut vous faire gagner du temps et de la raison plus tard lorsque vous testez et retestez votre modèle. Même avec une préparation minutieuse, vous devrez peut-être encore réviser votre modèle de manière flexible au fur et à mesure que vous régressez et identifier les variables qui sont significatives et non.
Deux remarques importantes lors de la sélection de variables indépendantes :
- Les variables indépendantes doivent avoir une relation logique et concevable avec la variable dépendante (c'est-à-dire les précipitations moyennes à Tokyo et le nombre de crises cardiaques dans le Wisconsin seraient en bas de ma liste de corrélations à examiner)
- Les variables indépendantes ne doivent pas être fortement corrélées les unes aux autres (c'est-à-dire que l'inclusion du coût, des clics et du CPC en tant que variables indépendantes dans la même régression entraînerait une erreur de multicolinéarité dans le modèle)
Dans notre exemple, nous voulons examiner ce qui motive le CPA de notre compte. Nous savons qu'il existe deux réseaux sur lesquels nous diffusons des annonces dans Adwords : les Réseaux de Recherche et Display, et nous savons que les deux principales variables qui déterminent le CPA (Coût/Conversion) pour chaque réseau sont le CPC (Coût/Clic) et le CVR (Conversion/Clic ).
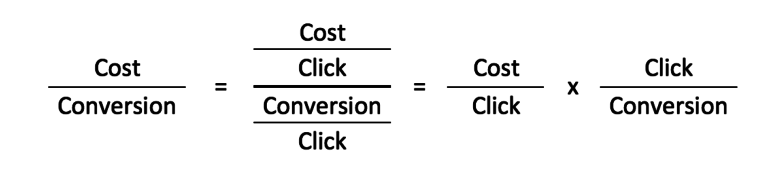
Par conséquent, nous commencerons par régresser séparément le CPA sur le CPC et le CVR pour la recherche et le display afin de déterminer quelles variables indépendantes sont significatives et devraient donc être incluses dans notre modèle final.
Étape 3 : Régresser et réviser
Pour exécuter une régression dans Excel :
1. Avant de lancer la régression dans Excel, vérifiez d'abord que les variables indépendantes (colonnes de données) sont voisines les unes des autres.
2. Ensuite, confirmez que le module complémentaire « Analysis ToolPak » est activé pour Excel (visible dans le ruban « Données » une fois activé).
3. Dans la boîte à outils d'analyse de données, sélectionnez « Régression ».
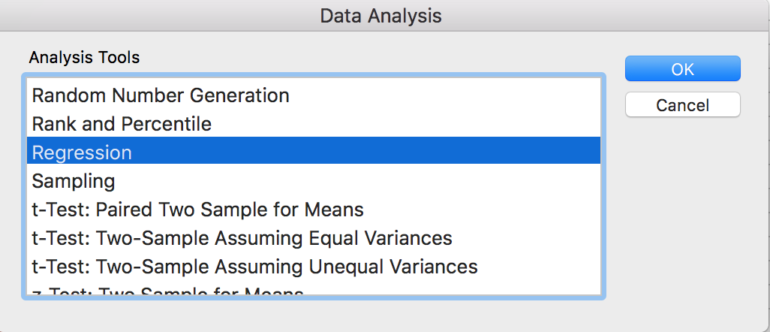
4. Saisissez votre plage de variables dépendantes (Y) et votre plage de variables indépendantes (X), en sélectionnant « Étiquettes » si vous choisissez d'inclure les en-têtes de colonne
5. Sélectionnez un emplacement pour votre sortie de régression (une feuille de calcul nouvelle ou existante)
6. Sélectionnez « résidus » si vous souhaitez rechercher et supprimer les valeurs aberrantes dans les données
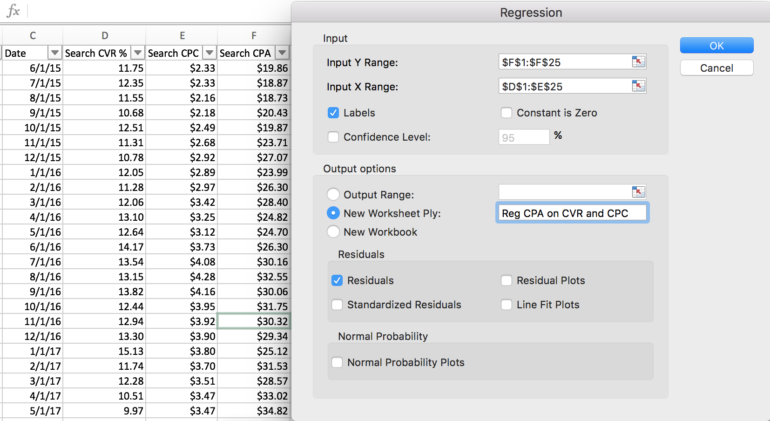
7. Cliquez sur « OK » pour exécuter la régression. Vous serez automatiquement dirigé vers la feuille contenant le résumé et les détails de la sortie.
8. Si l'examen de la sortie de régression révèle des variables indépendantes non significatives (généralement, les valeurs p sont supérieures à 0,1) ou un R-carré inférieur aux attentes (voir « A » ci-dessous), vous pouvez répéter le processus au besoin pour affiner le modèle.
Étape 4 : Comprendre la sortie
Regarder un résultat récapitulatif pour la première fois peut être intimidant et décourageant. Pour faciliter les choses, les sections clés de la sortie sont mises en évidence ci-dessous pour vous aider à évaluer le modèle que votre régression vient de construire.

(A) R carré et R carré ajusté : il s'agit d'une mesure de l'adéquation de votre modèle aux données. En bref, R Square indique dans quelle mesure la variation de la variable dépendante est expliquée par les variables indépendantes choisies. Le carré R ajusté est fondamentalement le même, mais prend également en compte le nombre de variables indépendantes incluses, fournissant une mesure légèrement plus précise. (Il n'y a pas de "bon" ou "bon" R Square, car cela dépend du type de modèle et de données que vous utilisez, mais plus il est haut, mieux c'est).
(B) Erreur standard : La racine carrée de la somme des différences au carré entre les résultats prévus et réels. Pour une distribution normale, environ 65 % des résidus (voir « E » ci-dessous) seront inférieurs à une erreur standard et 95 % seront inférieurs à 2. Les résidus supérieurs à deux fois l'erreur standard sont généralement étiquetés comme des valeurs aberrantes dans les données.
(C) Coefficients des variables indépendantes : les coefficients sont les termes « A » dans votre formule de régression. Ainsi, pour cet exemple, une augmentation d'une unité du CPC devrait être égale à une augmentation de 8,4 du CPA (en supposant que le CVR reste constant).
(D) Valeur P des variables indépendantes : En termes simples, la valeur P indique la signification de la variable indépendante. Les valeurs P faibles sont significatives (visant moins de 0,1), tandis que les valeurs P élevées indiquent que la corrélation perçue pourrait être purement fortuite. Les variables indépendantes avec des valeurs p élevées doivent être exclues pendant l'étape de « révision flexible ».
(E) Résidus : Ceci montre la différence entre la valeur prédite de la variable dépendante pour chaque itération et la valeur réelle enregistrée. Comme mentionné ci-dessus, la plupart des résidus devraient être inférieurs à 1 erreur standard et presque tous devraient être inférieurs à la valeur de 2 * erreur standard. Vous pouvez décider d'inclure ou d'exclure les valeurs aberrantes identifiées (résidus supérieurs à deux fois l'erreur standard) de votre modèle.
Étape 5 : Assembler (la partie à emporter !)
Après avoir exécuté trois régressions, nous avons trouvé les trois équations suivantes reliant le CPC et le CVR sur les Réseaux de Recherche et Display au réseau et aux CPA totaux :



Ces équations vérifient ce que nous savions déjà (ou pensions savoir) : que les CPC et les CVR sur les Réseaux de Recherche et Display jouent tous un rôle important dans le comportement de notre CPA total. Au-delà de cela, cependant, ils ont également révélé 3 choses qu'une carte thermique standard ne ferait pas.
- Une augmentation du CPC sur le Réseau de Recherche a 3,5 fois plus d'impact sur le CPA sur le Réseau de Recherche qu'une augmentation équivalente du CVR sur le Réseau de Recherche
- Les fluctuations du CPC sur le Réseau Display ont presque 5 fois plus d'impact que le CVR sur le Réseau Display sur le CPA sur le Réseau Display
- Dans l'ensemble, les changements dans les performances du réseau Display affectent le CPA total de manière plus importante que les changements d'une ampleur similaire dans les performances du réseau de recherche
De là, il est clair que Display CPC est la cible n°1 pour l'optimisation si je vise à réduire le CPA total. Le CPC de recherche et le CVR d'affichage sont les suivants, avec le CVR de recherche la moindre de mes priorités.
Les régressions sont un outil puissant et un excellent ajout à la ceinture à outils du gestionnaire PPC. Cet exemple de base ne montre qu'une des nombreuses manières dont les régressions peuvent vous aider à comprendre les relations entre vos KPI préférés. Nous espérons que vous testerez ou continuerez à utiliser la fonction de régression d'Excel et que vous partagerez votre expérience/réflexions/résultats avec nous sur Twitter !
