Kutukan Dimensi
Diterbitkan: 2015-07-08Apa itu Kutukan Dimensi
Curse of Dimensionality mengacu pada sifat non-intuitif dari data yang diamati saat bekerja di ruang dimensi tinggi*, khususnya terkait dengan kegunaan dan interpretasi jarak dan volume. Ini adalah salah satu topik favorit saya dalam Pembelajaran Mesin dan Statistik karena memiliki aplikasi yang luas (tidak spesifik untuk metode pembelajaran mesin apa pun), ini sangat kontra-intuitif dan karenanya menakjubkan, memiliki aplikasi mendalam untuk teknik analitik apa pun, dan ia memiliki nama menakutkan 'keren' seperti kutukan Mesir!
Untuk pemahaman cepat, pertimbangkan contoh ini: Katakanlah, Anda menjatuhkan koin pada garis 100 meter. Bagaimana kamu menemukannya? Sederhana, hanya berjalan di garis dan mencari. Tapi bagaimana jika itu 100 x 100 m persegi. bidang? Sudah semakin sulit, mencoba mencari (kira-kira) lapangan sepak bola untuk satu koin. Tetapi bagaimana jika itu adalah ruang 100 x 100 x 100 m3?! Anda tahu, lapangan sepak bola sekarang memiliki ketinggian tiga puluh lantai. Semoga berhasil menemukan koin di sana! Itu, pada dasarnya adalah "kutukan dimensi".
Banyak metode ML menggunakan Pengukur Jarak
Sebagian besar metode segmentasi dan pengelompokan bergantung pada jarak komputasi antara pengamatan. Segmentasi k-Means yang terkenal memberikan titik ke pusat terdekat . Pengelompokan DBSCAN dan Hierarchical juga membutuhkan metrik jarak. Algoritme deteksi outlier berbasis distribusi dan kepadatan juga menggunakan jarak relatif terhadap jarak lain untuk menandai outlier.
Solusi klasifikasi terawasi seperti metode k-Nearest Neighbors juga menggunakan jarak antar observasi untuk menetapkan kelas ke observasi yang tidak diketahui. Metode Support Vector Machine melibatkan transformasi pengamatan di sekitar Kernel terpilih berdasarkan jarak antara pengamatan dan kernel.
Bentuk umum dari sistem rekomendasi melibatkan kesamaan berbasis jarak antara vektor atribut pengguna dan item. Bahkan ketika bentuk jarak lain digunakan, jumlah dimensi memainkan peran dalam desain analitik.
Salah satu metrik jarak yang paling umum adalah metrik Jarak Euclidian, yang merupakan jarak linier antara dua titik dalam ruang hiper multidimensi. Jarak Euclidian untuk titik i dan titik j dalam ruang berdimensi n dapat dihitung sebagai:
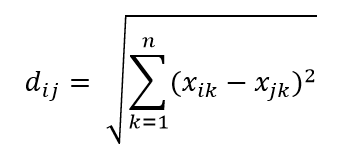
Jarak memainkan malapetaka di dimensi tinggi
Pertimbangkan proses pengambilan sampel data yang sederhana. Misalkan kotak luar hitam pada Gambar 1 adalah alam semesta data dengan distribusi titik data yang seragam di seluruh volume, dan bahwa kita ingin mengambil sampel 1% dari pengamatan yang diapit oleh kotak merah di dalam. Kotak hitam adalah hiper-kubus dalam ruang multi-dimensi dengan masing-masing sisi mewakili rentang nilai dalam dimensi itu. Untuk contoh 3 dimensi sederhana pada Gambar. 1, kita mungkin memiliki rentang berikut:
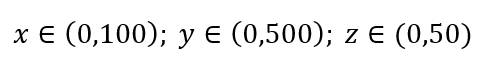
Gambar 1: Pengambilan Sampel
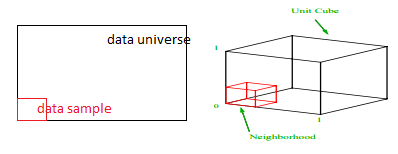
Berapa proporsi setiap rentang yang harus kita sampel untuk mendapatkan sampel 1% itu? Untuk 2-dimensi, 10% rentang akan mencapai keseluruhan sampel 1%, jadi kami dapat memilih x∈(0,10) dan y∈(0,50) dan berharap dapat menangkap 1% dari semua pengamatan. Ini karena 10%2=1%. Apakah Anda mengharapkan proporsi ini lebih tinggi atau lebih rendah untuk 3 dimensi?
Meskipun pencarian kami sekarang ke arah tambahan, proporsional sebenarnya meningkat menjadi 21,5%. Dan tidak hanya meningkat, hanya untuk satu dimensi tambahan, itu berlipat ganda! Dan Anda dapat melihat bahwa kita harus menutupi hampir seperlima dari setiap dimensi hanya untuk mendapatkan seperseratus dari keseluruhan! Dalam 10-dimensi, proporsi ini adalah 63% dan dalam 100-dimensi – yang merupakan jumlah dimensi yang tidak biasa dalam pembelajaran mesin kehidupan nyata mana pun – seseorang harus mengambil sampel 95% dari rentang di setiap dimensi untuk mengambil sampel 1% dari pengamatan! Hasil yang membingungkan ini terjadi karena dalam dimensi tinggi penyebaran titik data menjadi lebih besar meskipun tersebar secara seragam.

Ini memiliki konsekuensi dalam hal desain eksperimen dan pengambilan sampel. Proses menjadi sangat mahal secara komputasi, bahkan sampai pengambilan sampel secara asimtotik mendekati populasi meskipun ukuran sampel tetap jauh lebih kecil daripada populasi.
Pertimbangkan konsekuensi besar lainnya dari dimensi tinggi. Banyak algoritma mengukur jarak antara dua titik data untuk menentukan semacam kedekatan ( DBSCAN , Kernel, k-Nearest Neighbour) mengacu pada beberapa ambang jarak yang telah ditentukan sebelumnya. Dalam 2-dimensi, kita dapat membayangkan bahwa dua titik dekat jika satu jatuh dalam radius tertentu dari yang lain. Perhatikan gambar kiri pada Gambar. 2. Berapa bagian dari titik-titik yang berjarak seragam di dalam kotak hitam yang berada di dalam lingkaran merah? Itu tentang
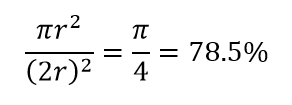
Gambar 2: Kedekatan
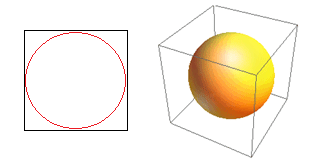
Jadi, jika Anda memasukkan lingkaran terbesar yang mungkin di dalam bujur sangkar, Anda menutupi 78% persegi. Namun, bola terbesar yang mungkin di dalam kubus hanya mencakup
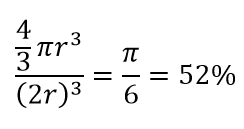
dari volume. Volume ini berkurang secara eksponensial menjadi 0,24% hanya untuk 10-dimensi! Apa yang pada dasarnya berarti bahwa di dunia dimensi tinggi setiap titik data berada di sudut dan tidak ada yang benar-benar merupakan pusat volume, atau dengan kata lain, volume pusat berkurang menjadi nol karena (hampir) tidak ada pusat! Ini memiliki konsekuensi besar dari algoritma pengelompokan berbasis jarak. Semua jarak mulai terlihat sama dan jarak apa pun yang lebih atau kurang dari yang lain adalah fluktuasi data yang lebih acak daripada ukuran ketidakmiripan apa pun!
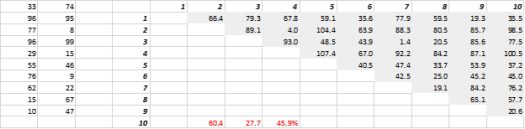
Gambar 3 menunjukkan data 2-D yang dihasilkan secara acak dan jarak semua-ke-semua yang sesuai. Koefisien Variasi Jarak, dihitung sebagai Standar Deviasi dibagi Mean, adalah 45,9%. Jumlah yang sesuai dari data 5-D yang dihasilkan serupa adalah 26,5% dan untuk 10-D adalah 19,1%. Memang ini adalah satu sampel, tetapi tren mendukung kesimpulan bahwa dalam dimensi tinggi setiap jarak hampir sama, dan tidak ada yang dekat atau jauh!
Gambar 3: Pengelompokan Jarak
Dimensi tinggi mempengaruhi hal-hal lain juga
Selain jarak dan volume, jumlah dimensi menciptakan masalah praktis lainnya. Persyaratan run-time dan sistem-memori solusi sering kali meningkat secara non-linier dengan peningkatan jumlah dimensi. Karena peningkatan eksponensial dalam solusi yang layak, banyak metode optimasi tidak dapat mencapai optima global dan harus dilakukan dengan optima lokal. Lebih lanjut, alih-alih solusi bentuk tertutup, optimasi harus menggunakan algoritma berbasis pencarian seperti penurunan gradien, algoritma genetika dan simulasi anil. Lebih banyak dimensi memperkenalkan kemungkinan korelasi dan estimasi parameter dapat menjadi sulit dalam pendekatan regresi.
Berurusan dengan Dimensi Tinggi
Ini akan menjadi posting blog tersendiri, tetapi analisis korelasi, pengelompokan, nilai informasi, faktor inflasi varians, analisis komponen utama adalah beberapa cara di mana jumlah dimensi dapat dikurangi.
* Jumlah variabel, pengamatan atau fitur titik data terdiri dari disebut dimensi data. Misalnya, setiap titik dalam ruang dapat direpresentasikan menggunakan 3 koordinat panjang, lebar, dan tinggi, dan memiliki 3 dimensi
