Estimasi Densitas menggunakan Histogram

Probability Density Functions (PDFs) menggambarkan probabilitas mengamati beberapa variabel acak kontinu di beberapa wilayah ruang. Untuk variabel acak satu dimensi X, ingat bahwa PDF f(x) mengikuti sifat-sifat yang

Probabilitas bahwa variabel mengambil nilai antara

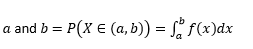
Probabilitas bahwa variabel mengambil nilai persis sama dengan

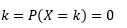
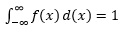
Memperkirakan PDF tersebut dari sampel pengamatan adalah masalah umum dalam Pembelajaran Mesin. Ini berguna dalam banyak algoritme deteksi outlier di mana kami berusaha memperkirakan distribusi "benar" berdasarkan pengamatan sampel dan kemudian mengklasifikasikan beberapa pengamatan yang ada atau baru sebagai outlier atau tidak. Misalnya, perusahaan asuransi mobil yang tertarik untuk menangkap penipuan mungkin memeriksa permintaan jumlah klaim untuk setiap jenis pekerjaan bodi, katakanlah, penggantian bumper, dan menandai potensi penipuan dengan jumlah yang terlalu tinggi. Melalui contoh lain, seorang psikolog anak dapat memeriksa waktu yang dibutuhkan untuk menyelesaikan tugas yang diberikan pada anak-anak yang berbeda dan menandai anak-anak yang membutuhkan waktu terlalu lama atau terlalu pendek untuk penyelidikan potensial.

Dalam posting blog ini, kami membahas bagaimana kami dapat mempelajari PDF dari sampel pengamatan , sehingga kami dapat menghitung probabilitas untuk setiap pengamatan dan memutuskan apakah itu sering atau jarang terjadi.

Estimasi Densitas menggunakan Histogram

Pertama kita menghasilkan beberapa data acak untuk demonstrasi.

set.seed(123)
data <- c(rnorm(200, 10, 20), rnorm(200, 60, 30), runif(200, 120, 180)) # 600 points

Selanjutnya, kami memvisualisasikannya untuk pemahaman kami, menggunakan histogram, seperti pada Gambar 1.

# Plot 1
hist(data, breaks=50, freq=F, main="Univariate Distribution", xlab="Data Value")
# Plot 2
hist(data, breaks=20, freq=F, main="", xlab="20 Data Bins", col='red', border='red')
par(new=T)
hist(data, breaks=100, freq=F, main="Univariate Distribution", xlab=NULL, xaxt='n', yaxt='n')

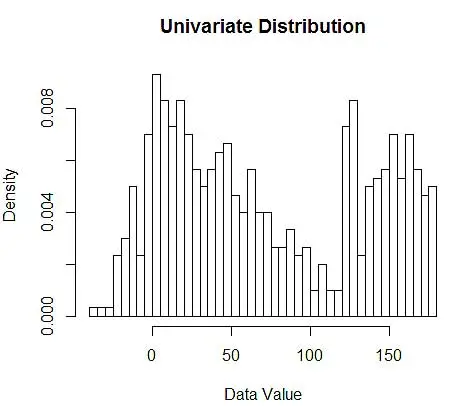
Meskipun histogram adalah bagan untuk visualisasi data, Anda juga dapat melihat bahwa itu adalah perkiraan pertama kami tentang kepadatan. Lebih khusus lagi, kita dapat memperkirakan densitas dengan membagi data ke dalam bin dan mengasumsikan bahwa densitas konstan dalam rentang bin itu dan memiliki nilai yang sama dengan jumlah pengamatan yang masuk ke dalam bin itu sebagai proporsi dari jumlah total pengamatan.

Oleh karena itu, perkiraan PDF adalah

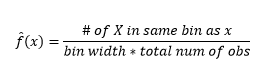
Dan Anda menyadari bahwa Anda telah membuat asumsi tentang bin-width yang akan mempengaruhi perkiraan kepadatan. Oleh karena itu bin-width merupakan parameter untuk model pendugaan densitas menggunakan histogram . Namun, fakta yang diabaikan adalah bahwa kami juga bekerja dengan satu parameter lagi – yang merupakan posisi awal bin pertama . Anda dapat melihat bagaimana hal itu dapat memengaruhi estimasi kepadatan untuk semua tempat sampah. Untuk melihat dampak lebar bin, Gambar 2 menutupi perkiraan kepadatan dengan histogram 20-bin dan 100-bin. Lihatlah daerah yang dilingkari, di mana bin yang lebih sedikit/lebih kasar memberikan perkiraan kepadatan yang datar, sementara banyak/tempat yang lebih halus memberikan perkiraan kepadatan yang bervariasi. Untuk titik kuning, perkiraan kepadatan akan berkisar dari 0,004 hingga 0,008 dari dua model yang berbeda.

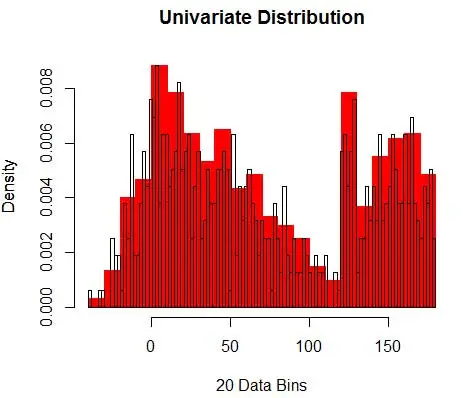
Oleh karena itu, pemilihan parameter yang tepat sangat penting untuk mendapatkan estimasi densitas yang tepat. Kami akan membahasnya, tetapi perhatikan bahwa ada juga masalah lain dengan histogram. Perkiraan kepadatan menggunakan histogram cukup tersentak-sentak dan terputus-putus . Kepadatan datar untuk bin dan kemudian tiba-tiba berubah drastis untuk titik yang sangat kecil di luar bin. Hal ini membuat konsekuensi dari perkiraan yang salah bahkan lebih buruk untuk masalah praktis.

Terakhir, kami telah bekerja dengan variabel satu dimensi untuk kemudahan ilustrasi, tetapi dalam praktiknya sebagian besar masalah adalah multi-dimensi. Karena jumlah bin tumbuh secara eksponensial dengan jumlah dimensi, jumlah pengamatan yang diperlukan untuk memperkirakan densitas juga bertambah . Faktanya, masuk akal bahwa meskipun memiliki jutaan pengamatan, banyak tempat sampah tetap kosong atau berisi pengamatan satu digit. Dengan hanya 50 tempat sampah masing-masing hanya dalam 3 dimensi, kami memiliki 503=125.000 sel yang perlu diisi. Itu berarti rata-rata 8 pengamatan per sel, dengan asumsi distribusi seragam, satu juta data pelatihan pengamatan.

Bagaimana cara memilih parameter yang tepat?

Untuk bin-width n jumlah pengamatan N untuk bin J proporsi pengamatan adalah

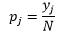
dan perkiraan kepadatan adalah

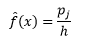
Teori statistik membuktikan bahwa sementara f(x) adalah nilai densitas yang diharapkan dalam bin, varians densitas adalah

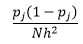
Meskipun kita bisa mendapatkan estimasi kepadatan yang lebih baik dengan mengurangi bin-width n , kita meningkatkan varians estimasi, karena kita dapat secara intuitif merasakan tentang bin-width yang terlalu halus. Kita dapat menggunakan teknik validasi silang keluar satu untuk memperkirakan set parameter yang optimal. Kita dapat memperkirakan kepadatan menggunakan semua pengamatan kecuali satu, dan kemudian menghitung kepadatan dari pengamatan yang ditinggalkan dan kesalahan pengukuran dalam estimasi. Memecahkan ini secara matematis untuk histogram memberikan solusi bentuk tertutup untuk fungsi kerugian untuk lebar bin yang diberikan.

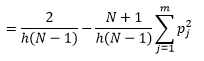
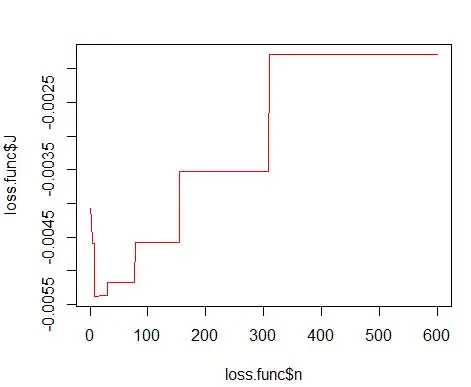
di mana m adalah jumlah kotak. Rincian teknis di atas ada dalam kuliah ini [pdf] . Kita dapat memplot fungsi kerugian ini untuk berbagai jumlah tempat sampah (Gambar 3)

getLoss <- function(n.break) {
N <- 600
res <- hist(data, breaks=n.break, freq=F)
bin <- as.numeric(res$breaks)
h <- bin[2]-bin[1]
p <- res$density
p <- p * h
return ( 2/(h*(N-1)) - ( (N+1)/(h*(N-1))*sum(p*p) ) )
}
loss.func <- data.frame(n=1:600)
loss.func$J <- sapply(loss.func$n, function(x) getLoss(x))
# Plot 3
plot(loss.func$n, loss.func$J, col='red', type='l')
opt.break <- max(loss.func[loss.func$J == min(loss.func$J), 'n'])
print(opt.break)
# Plot 4
hist(data, breaks=opt.break, freq=F, main="Univariate Distribution", xlab="15 Data Bins")

dan dapatkan angka optimal sebagai 15. Sebenarnya apa pun dari 8-15 baik-baik saja.

Akibatnya, di bawah Gambar 4 adalah estimasi densitas yang menyeimbangkan nilai densitas serta granularitas (dengan tradeoff bias-varians optimal).

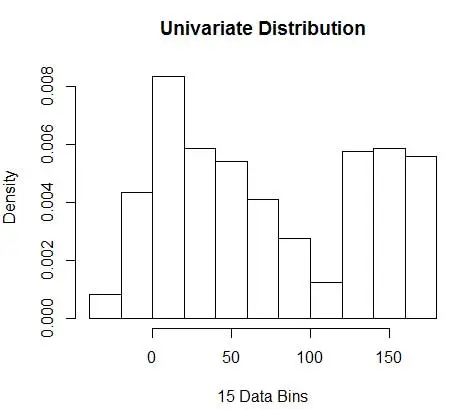
Jika Anda merasa sedikit tidak nyaman pada saat ini maka saya bersama Anda. Meskipun jumlah bins secara matematis optimal, rasanya perkiraan yang terlalu kasar. Tidak ada perasaan intuitif mengapa kami telah melakukan pekerjaan terbaik. Dan jangan lupakan kekhawatiran lain tentang posisi awal, estimasi terputus-putus, dan kutukan dimensi. Jangan putus asa, ada cara yang lebih baik. Dalam posting berikutnya kita akan berbicara tentang Estimasi Densitas menggunakan Kernel.