Mengukur Jarak di Hyperspace

Siapa pun yang akrab dengan teknik analitik akan memperhatikan banyak algoritme yang mengandalkan jarak di antara titik data untuk aplikasi mereka. Setiap pengamatan, atau contoh data, biasanya direpresentasikan sebagai vektor multidimensi, dan input ke algoritma memerlukan jarak antara setiap pasangan pengamatan tersebut.

Metode perhitungan jarak tergantung pada jenis data – numerik, kategorikal, atau campuran. Beberapa algoritma hanya berlaku untuk satu kelas pengamatan, sementara yang lain bekerja pada banyak. Dalam posting ini, kita akan membahas ukuran jarak yang bekerja pada data numerik. Mungkin ada lebih banyak cara jarak dapat diukur dalam hyperspace multi-dimensi daripada yang dapat dicakup dalam satu posting blog, dan seseorang selalu dapat menemukan cara yang lebih baru, tetapi kami melihat beberapa metrik jarak umum dan manfaat relatifnya.

Untuk tujuan sisa posting blog, kami menyiratkan

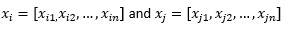
untuk merujuk pada dua pengamatan atau vektor data.

Siapkan dulu datanya…

Sebelum kita meninjau metrik jarak yang berbeda, kita perlu menyiapkan data:

Transformasi ke vektor numerik

Untuk pengamatan campuran, yang berisi dimensi numerik dan kategorik, langkah pertama adalah benar-benar mengubah dimensi kategoris menjadi dimensi numerik. Dimensi kategoris dengan tiga nilai potensial dapat diubah menjadi dua atau tiga dimensi numerik dengan nilai biner. Karena variabel kategoris ini harus mengambil salah satu dari tiga nilai, salah satu dari tiga dimensi numerik akan berkorelasi sempurna dengan dua lainnya. Ini mungkin atau mungkin tidak baik-baik saja tergantung pada aplikasi Anda.

Jika pengamatan murni kategoris, seperti string teks (kalimat panjang yang bervariasi) atau urutan genom (urutan panjang tetap), maka beberapa metrik jarak khusus dapat langsung diterapkan tanpa mengubah data ke dalam format numerik. Kami akan membahas algoritma ini di posting berikutnya.

Normalisasi

Bergantung pada kasus penggunaan Anda, Anda mungkin ingin menormalkan setiap dimensi pada skala yang sama, sehingga jarak di sepanjang satu dimensi tidak terlalu memengaruhi jarak keseluruhan antara pengamatan. Hal yang sama juga dibahas pada algoritma k-Means. Ada dua jenis normalisasi yang mungkin:

Normalisasi rentang (rescaling) menormalkan data berada dalam rentang 0-1, dengan cara mengurangkan nilai minimum dari setiap dimensi kemudian membaginya dengan rentang nilai dalam dimensi tersebut.

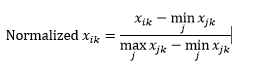
Masalah pertama dengan normalisasi rentang adalah bahwa nilai yang tidak terlihat dapat dinormalisasi di luar rentang 0-1. Padahal, ini umumnya tidak menjadi perhatian untuk sebagian besar metrik jarak, tetapi jika algoritme tidak dapat menangani nilai negatif maka ini bisa menjadi masalah. Masalah kedua adalah bahwa ini sangat tergantung pada outlier. Jika satu pengamatan memiliki nilai yang sangat ekstrem (tinggi atau rendah) untuk suatu dimensi, nilai yang dinormalisasi untuk dimensi tersebut untuk pengamatan lain akan diringkas bersama dan kehilangan kekuatan diskriminatifnya.

Normalisasi standar (z-scaling) menormalkan dimensi menjadi 0 mean dan 1 standar deviasi, dengan mengurangkan mean dari dimensi tersebut dari setiap pengamatan dan kemudian membaginya dengan standar deviasi nilai dimensi tersebut di semua pengamatan.

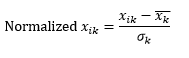
Ini umumnya menyimpan data dalam kisaran -5 hingga +5, secara kasar, dan menghindari pengaruh nilai ekstrem.

Kami telah mensimulasikan penskalaan z dari dua pengamatan. Disimulasikan, karena kita benar-benar membutuhkan lebih dari dua pengamatan untuk menghitung rata-rata dan simpangan baku setiap dimensi, dan kita telah mengasumsikan kedua angka ini untuk setiap dimensi di sini.

Lalu hitung jaraknya…

Jarak Euclidean – alias jarak “saat burung gagak terbang” – adalah jarak terpendek dalam hyperspace multidimensi antara dua titik. Anda sudah familiar dengan ini di bidang 2D atau ruang 3D (ini adalah garis), tetapi konsep serupa meluas ke dimensi yang lebih tinggi. Jarak Euclidean antara vektor dalam ruang n-dimensi dihitung sebagai

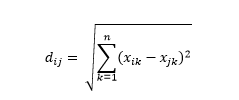
Untuk contoh vektor data yang diubah, ini adalah

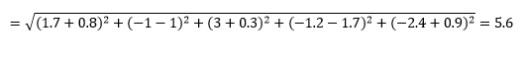
Ini adalah metrik yang paling umum dan seringkali sangat cocok untuk sebagian besar aplikasi. Varian dari ini adalah jarak kuadrat-Euclidean, yang hanya merupakan jumlah dari selisih kuadrat.

Jarak Manhattan – dinamai karena jaringan Timur-Barat-Utara-Selatan seperti struktur jalan-jalan Manhattan di New York – adalah jarak antara dua titik ketika melintasi sejajar dengan sumbu.

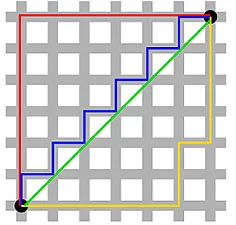
Jarak Manhattan
Jarak Euclidean

Ini dihitung sebagai

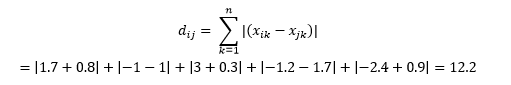
Ini mungkin berguna dalam beberapa aplikasi di mana jarak digunakan dalam arti fisik yang nyata daripada pengertian pembelajaran mesin tentang "ketidakmiripan". Misalnya, jika Anda perlu menghitung jarak yang ditempuh mobil pemadam kebakaran untuk mencapai suatu titik, maka menggunakan ini lebih praktis.

Jarak Canberra adalah varian tertimbang dari jarak Manhattan, dan dihitung sebagai

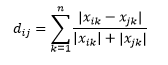
Jarak norma-L adalah perpanjangan dari dua di atas – atau Anda dapat mengatakan bahwa di atas dua adalah kasus khusus dari jarak norma-L – dan didefinisikan sebagai

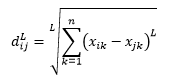
di mana L adalah bilangan bulat positif. Saya belum menemukan kasus di mana saya perlu menggunakan ini, tetapi ini masih bagus untuk mengetahui kemungkinan. Misalnya jarak 3-norma adalah

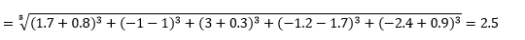
Perhatikan bahwa L umumnya harus bilangan bulat genap karena kita tidak ingin kontribusi jarak positif atau negatif dibatalkan.

Jarak Minkowski adalah generalisasi dari jarak norma-L, di mana L dapat mengambil nilai apa pun dari 0 hingga memasukkan nilai pecahan. Jarak minkowski orde p didefinisikan sebagai

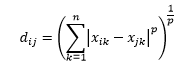
Jarak cosinus adalah ukuran sudut antara dua vektor, masing-masing mewakili dua pengamatan, dan dibentuk dengan menggabungkan titik data ke titik asal. Jarak kosinus berkisar dari 0 (persis sama) hingga 1 (tidak ada koneksi), dan dihitung sebagai:

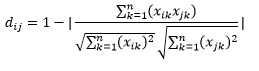
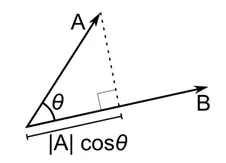
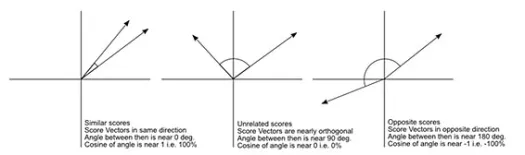
Meskipun ini adalah ukuran jarak yang lebih umum ketika bekerja dengan data kategorikal, ini juga dapat didefinisikan untuk vektor numerik. Untuk vektor numerik kami, ini akan menjadi

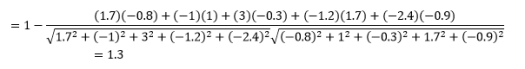
Tapi ingat peringatannya…

Anda tahu ini akan datang, bukan? Jika analitik hanyalah sekumpulan rumus matematika, kami tidak membutuhkan orang pintar seperti Anda untuk melakukannya.

Hal pertama yang perlu diperhatikan adalah bahwa jarak yang dihitung oleh metrik yang berbeda berbeda. Anda mungkin tergoda untuk berpikir bahwa jarak Cosinus 1,3 adalah yang terkecil dan karenanya menunjukkan vektor yang paling dekat tetapi ini bukan cara yang tepat untuk menafsirkannya. Jarak antar metode yang berbeda tidak dapat dibandingkan, dan hanya jarak antara pasangan pengamatan yang berbeda dengan metode yang sama yang dapat dibandingkan. Jarak memiliki makna relatif dan tidak memiliki makna absolut dengan sendirinya .

Ini mengarah ke pertanyaan berikutnya tentang bagaimana memilih metrik jarak yang tepat. Sayangnya, tidak ada jawaban yang benar. Tergantung pada jenis data, konteks, masalah bisnis, aplikasi, dan metode pelatihan model, metrik yang berbeda memberikan hasil yang berbeda. Anda harus menggunakan penilaian, membuat asumsi, atau menguji kinerja model untuk memutuskan metrik yang tepat .

Peringatan kedua adalah yang sering saya ulangi tentang kutukan dimensi. Dalam dimensi yang lebih tinggi, jarak tidak berperilaku seperti yang kita pikirkan secara intuitif , dan analis harus sangat berhati-hati saat menggunakan metrik apa pun.

Peringatan ketiga adalah tentang hubungan antara jarak antara tiga pengamatan. Beberapa metrik mendukung ketidaksetaraan segitiga dan sementara yang lain tidak . Pertidaksamaan segitiga menyiratkan bahwa selalu terpendek untuk pergi dari titik i ke titik j secara langsung, daripada melalui titik perantara mana pun k. Secara matematis,

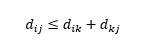
Bergantung pada aplikasi Anda, ini mungkin atau mungkin tidak memerlukan properti metrik jarak.

Oh, satu hal lagi, "jarak" adalah kebalikan dari "kesamaan". Semakin tinggi jarak, semakin rendah kesamaan, dan sebaliknya. Algoritma pengelompokan bekerja pada jarak, dan algoritma rekomendasi bekerja pada kesamaan, tetapi pada dasarnya mereka berbicara tentang hal yang sama.

Jadi, bagaimana Anda bisa mengubah nomor jarak menjadi nomor kesamaan?