Maledizione della dimensionalità
Pubblicato: 2015-07-08Cos'è la maledizione della dimensionalità
La maledizione della dimensionalità si riferisce alle proprietà non intuitive dei dati osservati quando si lavora in uno spazio ad alta dimensione*, in particolare in relazione all'usabilità e all'interpretazione di distanze e volumi. Questo è uno dei miei argomenti preferiti in Machine Learning e Statistica poiché ha ampie applicazioni (non specifiche per alcun metodo di apprendimento automatico), è molto controintuitivo e quindi impressionante, ha una profonda applicazione per qualsiasi tecnica di analisi e ha un nome spaventoso "cool" come una maledizione egiziana!
Per una rapida comprensione, considera questo esempio: supponiamo di aver lasciato cadere una moneta su una linea di 100 metri. Come lo trovi? Semplice, basta camminare sulla linea e cercare. E se fosse 100 x 100 mq. campo? Sta già diventando difficile, cercare di cercare un campo da calcio (approssimativamente) per una singola moneta. E se fosse 100 x 100 x 100 m3 di spazio?! Sai, il campo da calcio ora ha un'altezza di trenta piani. Buona fortuna a trovare una moneta lì! Questa, in sostanza, è "maledizione della dimensionalità".
Molti metodi ML utilizzano la misurazione della distanza
La maggior parte dei metodi di segmentazione e raggruppamento si basa sul calcolo delle distanze tra le osservazioni. La ben nota segmentazione k-Means assegna punti al centro più vicino. DBSCAN e il clustering gerarchico richiedevano anche metriche di distanza. Gli algoritmi di rilevamento dei valori anomali basati sulla distribuzione e sulla densità utilizzano anche la distanza rispetto ad altre distanze per contrassegnare i valori anomali.
Anche le soluzioni di classificazione supervisionate come il metodo k-Nearest Neighbors utilizzano la distanza tra le osservazioni per assegnare la classe all'osservazione sconosciuta. Il metodo Support Vector Machine prevede la trasformazione delle osservazioni attorno a kernel selezionati in base alla distanza tra l'osservazione e il kernel.
La forma comune di sistemi di raccomandazione implica la somiglianza basata sulla distanza tra i vettori di attributi dell'utente e dell'elemento. Anche quando vengono utilizzate altre forme di distanze, il numero di dimensioni gioca un ruolo nella progettazione analitica.
Una delle metriche di distanza più comuni è la metrica della distanza euclidea, che è semplicemente la distanza lineare tra due punti nell'iperspazio multidimensionale. La distanza euclidea per il punto i e il punto j nello spazio n dimensionale può essere calcolata come:
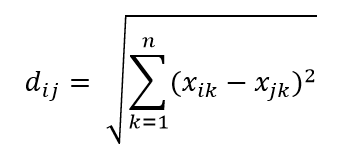
La distanza fa il caos in alta dimensione
Considera un semplice processo di campionamento dei dati. Supponiamo che il riquadro esterno nero in Fig. 1 sia un universo di dati con una distribuzione uniforme dei punti dati sull'intero volume e che vogliamo campionare l'1% delle osservazioni racchiuse da un riquadro rosso all'interno. La scatola nera è un ipercubo nello spazio multidimensionale con ciascun lato che rappresenta un intervallo di valori in quella dimensione. Per un semplice esempio tridimensionale in Fig. 1, potremmo avere il seguente intervallo:
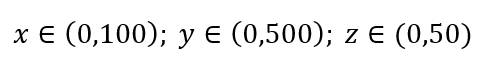
Figura 1: Campionamento
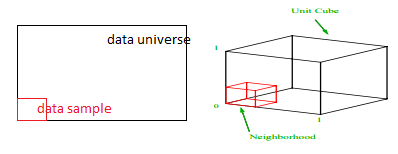
Qual è la proporzione di ciascun intervallo che dovremmo campionare per ottenere quel campione dell'1%? Per le 2 dimensioni, il 10% dell'intervallo raggiungerà un campionamento complessivo dell'1%, quindi possiamo selezionare x∈(0,10) e y∈(0,50) e aspettarci di catturare l'1% di tutte le osservazioni. Questo perché 10%2=1%. Ti aspetti che questa proporzione sia maggiore o minore per le 3 dimensioni?
Anche se la nostra ricerca è ora in una direzione aggiuntiva, il proporzionale aumenta effettivamente al 21,5%. E non solo aumenta, per una sola dimensione in più, raddoppia! E puoi vedere che dobbiamo coprire quasi un quinto di ogni dimensione solo per ottenere un centesimo del totale! In 10 dimensioni, questa proporzione è del 63% e in 100 dimensioni – che non è un numero raro di dimensioni in qualsiasi apprendimento automatico della vita reale – è necessario campionare il 95% dell'intervallo lungo ciascuna dimensione per campionare l'1% delle osservazioni! Questo risultato sbalorditivo si verifica perché in dimensioni elevate la diffusione dei punti dati diventa più ampia anche se sono distribuite uniformemente.

Ciò ha conseguenze in termini di progettazione dell'esperimento e campionamento. Il processo diventa molto costoso dal punto di vista computazionale, anche nella misura in cui il campionamento si avvicina asintoticamente alla popolazione nonostante la dimensione del campione rimanga molto più piccola della popolazione.
Consideriamo un'altra enorme conseguenza dell'elevata dimensionalità. Molti algoritmi misurano la distanza tra due punti dati per definire una sorta di vicinanza (DBSCAN, Kernel, k-Nearest Neighbour) in riferimento a una soglia di distanza predefinita. In 2 dimensioni, possiamo immaginare che due punti siano vicini se uno cade entro un certo raggio dell'altro. Considera l'immagine a sinistra in Fig. 2. Qual è la quota di punti uniformemente distanziati all'interno del quadrato nero che cade all'interno del cerchio rosso? Che riguarda
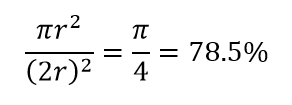
Figura 2: Vicinanza
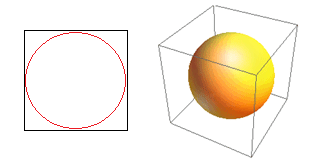
Quindi, se inserisci il cerchio più grande possibile all'interno del quadrato, copri il 78% del quadrato. Tuttavia, la sfera più grande possibile all'interno del cubo copre solo
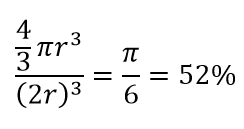
del volume. Questo volume si riduce esponenzialmente allo 0,24% per sole 10 dimensioni! Ciò che essenzialmente significa che nel mondo ad alta dimensione ogni singolo punto dati è agli angoli e nulla è davvero il centro del volume, o in altre parole, il volume del centro si riduce a nulla perché non c'è (quasi) nessun centro! Ciò ha enormi conseguenze degli algoritmi di clustering basati sulla distanza. Tutte le distanze iniziano a sembrare uguali e qualsiasi distanza maggiore o minore rispetto ad altre è una fluttuazione più casuale dei dati piuttosto che una misura di dissomiglianza!
La Fig. 3 mostra dati 2D generati casualmente e corrispondenti distanze totali. Il coefficiente di variazione della distanza, calcolato come deviazione standard divisa per la media, è 45,9%. Il numero corrispondente di dati 5-D generati in modo simile è 26,5% e per 10-D è 19,1%. È vero che questo è un campione, ma la tendenza supporta la conclusione che nelle dimensioni elevate ogni distanza è più o meno la stessa e nessuna è vicina o lontana!
Figura 3: Clustering della distanza
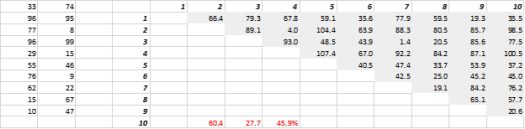
L'alta dimensione influenza anche altre cose
Oltre alle distanze e ai volumi, il numero delle dimensioni crea altri problemi pratici. I requisiti di runtime della soluzione e di memoria di sistema spesso aumentano in modo non lineare con l'aumento del numero di dimensioni. A causa dell'aumento esponenziale delle soluzioni fattibili, molti metodi di ottimizzazione non possono raggiungere l'optima globale e devono accontentarsi dell'optima locale. Inoltre, invece della soluzione in forma chiusa, l'ottimizzazione deve utilizzare algoritmi basati sulla ricerca come la discesa del gradiente, l'algoritmo genetico e la ricottura simulata. Più dimensioni introducono possibilità di correlazione e la stima dei parametri può diventare difficile negli approcci di regressione.
Trattare con l'alta dimensione
Questo sarà di per sé un post sul blog separato, ma l'analisi di correlazione, il raggruppamento, il valore delle informazioni, il fattore di inflazione della varianza, l'analisi delle componenti principali sono alcuni dei modi in cui è possibile ridurre il numero di dimensioni.
* Il numero di variabili, osservazioni o caratteristiche di cui è composto un punto dati è chiamato dimensione dei dati. Ad esempio, qualsiasi punto nello spazio può essere rappresentato utilizzando 3 coordinate di lunghezza, larghezza e altezza e ha 3 dimensioni
