Stima della densità mediante istogrammi

Le funzioni di densità di probabilità (PDF) descrivono la probabilità di osservare una variabile casuale continua in una certa regione dello spazio. Per la variabile casuale unidimensionale X, ricorda che PDF f(x) segue le proprietà che

Probabilità che la variabile prenda valori tra

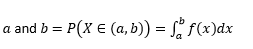
Probabilità che quella variabile assuma valori esattamente uguali

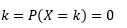
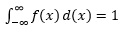
La stima di tale PDF da un campione di osservazioni è un problema comune in Machine Learning. Questo è utile in molti algoritmi di rilevamento dei valori anomali in cui cerchiamo di stimare la "vera" distribuzione sulla base di osservazioni campionarie e quindi classifichiamo alcune delle osservazioni esistenti o nuove come anomale o meno. Ad esempio, un assicuratore automobilistico interessato a rilevare una frode potrebbe esaminare la richiesta dell'importo del sinistro per ogni tipo di carrozzeria, ad esempio la sostituzione del paraurti, e contrassegnare per potenziale frode qualsiasi importo troppo alto. Per fare un altro esempio, uno psicologo infantile può esaminare il tempo impiegato per completare un determinato compito tra bambini diversi e contrassegnare quei bambini che impiegano troppo tempo o troppo poco tempo per potenziali indagini.

In questo post del blog, discutiamo come possiamo imparare il PDF da un campione di osservazioni , in modo da poter calcolare la probabilità per ogni osservazione e decidere se si tratta di un evento comune o raro.

Stima della densità utilizzando l'istogramma

Per prima cosa generiamo alcuni dati casuali per la dimostrazione.

set.seed(123)
data <- c(rnorm(200, 10, 20), rnorm(200, 60, 30), runif(200, 120, 180)) # 600 points

Successivamente, li visualizziamo per la nostra comprensione, utilizzando l'istogramma, come nella Figura 1.

# Plot 1
hist(data, breaks=50, freq=F, main="Univariate Distribution", xlab="Data Value")
# Plot 2
hist(data, breaks=20, freq=F, main="", xlab="20 Data Bins", col='red', border='red')
par(new=T)
hist(data, breaks=100, freq=F, main="Univariate Distribution", xlab=NULL, xaxt='n', yaxt='n')

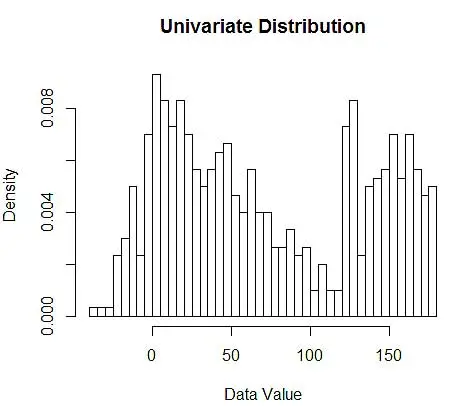
Sebbene gli istogrammi siano grafici per la visualizzazione dei dati, puoi anche vedere che sono la nostra prima stima della densità. Più specificamente, possiamo stimare la densità dividendo i dati in bin e assumendo che la densità sia costante all'interno di quell'intervallo di bin e abbia un valore uguale al numero di osservazioni che cadono in quel bin come proporzione del numero totale di osservazioni

Quindi, il PDF stimato lo è

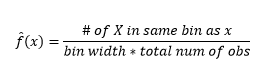
E ti rendi conto di aver fatto un'ipotesi sulla larghezza del contenitore che influirà sulla stima della densità. Quindi bin-width è un parametro per il modello di stima della densità che utilizza l'istogramma . Tuttavia, il fatto trascurato è che stiamo lavorando anche con un altro parametro, che è la posizione iniziale del primo bin . Puoi vedere come ciò può influenzare le stime della densità per tutti i bin. Per vedere l'impatto della larghezza del contenitore, la Figura 2 sovrappone le stime di densità con istogrammi a 20 e 100 contenitori. Osserva la regione circondata, dove un minor numero di contenitori/più grossolani fornisce una stima della densità piatta, mentre molti contenitori/più fini danno una stima di densità variabile. Per il punto giallo, le stime della densità variano da 0,004 a 0,008 da due diversi modelli.

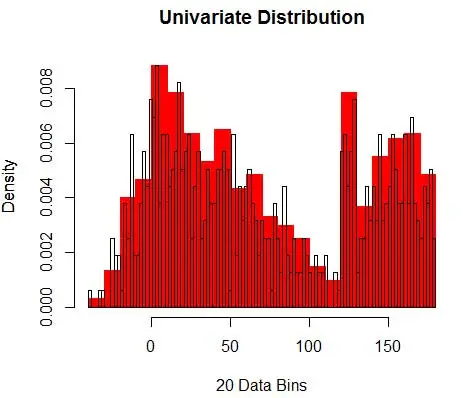
Pertanto, selezionare correttamente i parametri è fondamentale per ottenere la stima della densità corretta. Ci arriveremo, ma nota che ci sono anche altri problemi con gli istogrammi. Le stime della densità utilizzando gli istogrammi sono piuttosto a scatti e discontinue . La densità è piatta per un contenitore e poi cambia improvvisamente drasticamente per un punto infinitesimamente al di fuori del contenitore. Ciò rende la conseguenza di una stima errata ancora peggiore per problemi pratici.

Infine, abbiamo lavorato con una variabile monodimensionale per facilitare l'illustrazione, ma in pratica la maggior parte dei problemi sono multidimensionali. Poiché il numero di bin cresce esponenzialmente con il numero di dimensioni, cresce anche il numero di osservazioni necessarie per stimare la densità . In effetti, è plausibile che, nonostante abbiano milioni di osservazioni, molti contenitori rimangano vuoti o contengano osservazioni a una cifra. Con solo 50 contenitori ciascuno in sole 3 dimensioni, abbiamo 503=125000 celle che devono essere popolate. Ciò si traduce in una media di 8 osservazioni per cella, supponendo una distribuzione uniforme, un milione di dati di addestramento dell'osservazione.

Come selezionare i parametri giusti?

Per bin-width n numero di osservazioni N per bin J la proporzione di osservazioni è

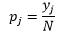
e la stima della densità è

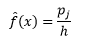
La teoria statistica dimostra che mentre f(x) è il valore atteso della densità nel contenitore, la varianza della densità lo è

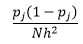
Mentre possiamo ottenere una migliore stima della densità riducendo la larghezza del bin n , aumentiamo la varianza della stima, poiché possiamo intuitivamente sentire una larghezza del bin troppo fine. Possiamo utilizzare la tecnica di convalida incrociata leave one-out per stimare l'insieme ottimale di parametri. Possiamo stimare la densità usando tutte le osservazioni tranne una, quindi calcolare la densità di quell'osservazione tralasciata e misurare l'errore nella stima. Risolvere questo problema matematicamente per gli istogrammi fornisce una soluzione in forma chiusa per la funzione di perdita per una determinata larghezza di bin.

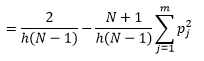
dove m è il numero di bin. I dettagli tecnici di cui sopra sono in questa lezione [pdf] . Possiamo tracciare questa funzione di perdita per vari numeri di contenitori (Figura 3)

getLoss <- function(n.break) {
N <- 600
res <- hist(data, breaks=n.break, freq=F)
bin <- as.numeric(res$breaks)
h <- bin[2]-bin[1]
p <- res$density
p <- p * h
return ( 2/(h*(N-1)) - ( (N+1)/(h*(N-1))*sum(p*p) ) )
}
loss.func <- data.frame(n=1:600)
loss.func$J <- sapply(loss.func$n, function(x) getLoss(x))
# Plot 3
plot(loss.func$n, loss.func$J, col='red', type='l')
opt.break <- max(loss.func[loss.func$J == min(loss.func$J), 'n'])
print(opt.break)
# Plot 4
hist(data, breaks=opt.break, freq=F, main="Univariate Distribution", xlab="15 Data Bins")

e ottieni il numero ottimale come 15. In realtà qualsiasi cosa da 8-15 va bene.

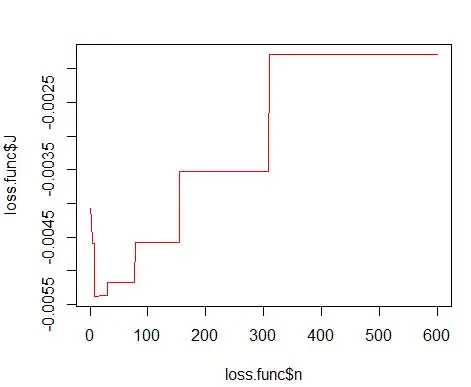
Di conseguenza, sotto la Figura 4 c'è una stima della densità che bilancia i valori di densità e la granularità (con un compromesso ottimale tra bias e varianza).

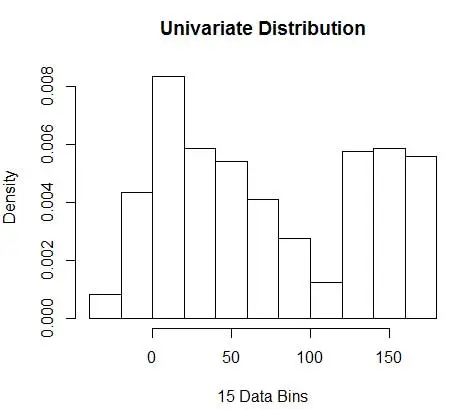
Se a questo punto ti senti un po' a disagio, allora sono con te. Anche se il numero di contenitori è matematicamente ottimale, sembra una stima troppo grossolana. Non c'è alcuna sensazione intuitiva del motivo per cui abbiamo fatto il miglior lavoro. E per non dimenticare altre preoccupazioni sulla posizione di partenza, la stima discontinua e la maledizione della dimensionalità. Non disperare, c'è un modo migliore. Nel prossimo post parleremo della stima della densità utilizzando i kernel.