Misurare la distanza nell'iperspazio

Chiunque abbia una conoscenza superficiale delle tecniche analitiche avrebbe notato molti algoritmi che si basano sulle distanze tra i punti dati per la loro applicazione. Ogni osservazione, o istanza di dati, è solitamente rappresentata come vettore multidimensionale e l'input per l'algoritmo richiede distanze tra ciascuna coppia di tali osservazioni.

Il metodo di calcolo della distanza dipende dal tipo di dati: numerici, categoriali o misti. Alcuni degli algoritmi si applicano a una sola classe di osservazioni, mentre altri funzionano su più. In questo post, discuteremo delle misure di distanza che funzionano su dati numerici. Ci sono forse più modi in cui la distanza può essere misurata nell'iperspazio multidimensionale rispetto a quelli che possono essere coperti in un singolo post sul blog, e si possono sempre inventare modi nuovi, ma esaminiamo alcune delle metriche di distanza comuni e i loro meriti relativi.

Ai fini del resto del post del blog, intendiamo

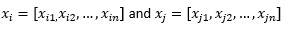
fare riferimento a due osservazioni o vettori di dati.

Per prima cosa prepara i dati...

Prima di esaminare diverse metriche di distanza, dobbiamo preparare i dati:

Trasformazione in vettore numerico

Per l'osservazione mista, che contiene dimensioni sia numeriche che categoriali, il primo passo è trasformare effettivamente la dimensione categoriale in dimensione/i numerica/i. Una dimensione categoriale con tre valori potenziali può essere trasformata in due o tre dimensioni numeriche con valori binari. Poiché questa variabile categoriale assume necessariamente uno dei tre valori, una delle tre dimensioni numeriche sarà perfettamente correlata con le altre due. Questo può o non può andare bene a seconda dell'applicazione.

Se l'osservazione è puramente categoriale, come una stringa di testo (frasi di lunghezza variabile) o una sequenza del genoma (sequenze di lunghezza fissa), è possibile applicare direttamente una metrica di distanza speciale senza trasformare i dati in formato numerico. Discuteremo questi algoritmi nel prossimo post.

Normalizzazione

A seconda del caso d'uso, potresti voler normalizzare ogni dimensione sulla stessa scala, in modo che la distanza lungo una qualsiasi dimensione non influisca indebitamente sulla distanza complessiva tra le osservazioni. La stessa cosa è stata discussa nell'algoritmo k-Means. Sono possibili due tipi di normalizzazione:

La normalizzazione dell'intervallo (ridimensionamento) normalizza i dati in modo che siano compresi nell'intervallo 0-1, sottraendo il valore minimo da ciascuna dimensione e quindi dividendo per l'intervallo di valori in quella dimensione.

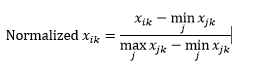
Il primo problema con la normalizzazione dell'intervallo è che un valore invisibile può essere normalizzato oltre l'intervallo 0-1. Tuttavia, questo generalmente non è un problema per la maggior parte delle metriche di distanza, ma se l'algoritmo non è in grado di gestire valori negativi, questo può essere un problema. Il secondo problema è che questo dipende fortemente dai valori anomali. Se un'osservazione ha un valore molto estremo (alto o basso) per una dimensione, il valore normalizzato per quella dimensione per le altre osservazioni sarà raggruppato insieme e perderà i loro poteri discriminatori.

La normalizzazione standard (ridimensionamento z) normalizza la dimensione in modo che abbia 0 media e 1 deviazione standard, sottraendo la media da quella dimensione di ciascuna osservazione e quindi dividendo per la deviazione standard del valore di quella dimensione in tutte le osservazioni.

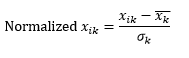
Questo generalmente mantiene i dati nell'intervallo da -5 a +5, approssimativamente, ed evita l'influenza di valori estremi.

Abbiamo simulato lo z-scaling di due osservazioni. Simulato, perché abbiamo davvero bisogno di molte più di due osservazioni per calcolare la media e la deviazione standard di ciascuna dimensione e abbiamo assunto entrambi questi numeri per ciascuna dimensione qui.

Poi calcola la distanza...

La distanza euclidea , nota anche come distanza "in linea d'aria", è la distanza più breve nell'iperspazio multidimensionale tra due punti. Hai familiarità con questo nel piano 2D o nello spazio 3D (questa è una linea), ma un concetto simile si estende a dimensioni superiori. La distanza euclidea tra i vettori nello spazio n-dimensionale è calcolata come

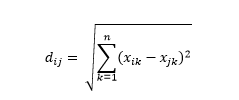
Per esempi di vettori di dati trasformati, questo è

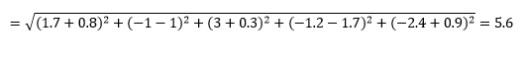
Questa è la metrica più comune e spesso molto adatta per la maggior parte delle applicazioni. Una variante di questo è la distanza euclidea al quadrato, che è solo la somma delle differenze al quadrato.

La distanza di Manhattan - chiamata così per la griglia Est-Ovest-Nord-Sud come la struttura delle strade di Manhattan a New York - è la distanza tra due punti quando attraversano parallelamente agli assi.

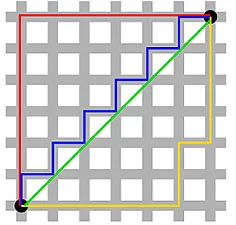
Distanza di Manhattan
Distanza euclidea

Questo è calcolato come

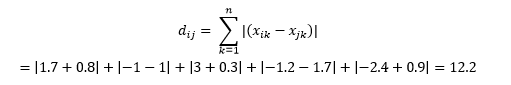
Questo può essere utile in alcune applicazioni in cui la distanza viene utilizzata in senso fisico reale piuttosto che nel senso di "dissomiglianza" dell'apprendimento automatico. Ad esempio, se è necessario calcolare la distanza percorsa dal camion dei pompieri per raggiungere un punto, l'utilizzo di questo è più pratico.

La distanza di Canberra è una variante ponderata della distanza di Manhattan e viene calcolata come

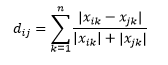
La distanza L-norma è un'estensione di sopra due - o si può dire che sopra due sono casi specifici di distanza L-norma - ed è definita come

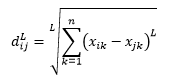
dove L è un numero intero positivo. Non mi sono imbattuto in casi in cui dovessi usarlo, ma è ancora bene conoscere la possibilità. Ad esempio, la distanza di 3 norme sarà

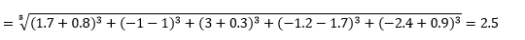
Si noti che L dovrebbe generalmente essere intero pari poiché non vogliamo che i contributi di distanza positivi o negativi si annullino.

La distanza di Minkowski è la generalizzazione della distanza della norma L, dove L potrebbe assumere qualsiasi valore da 0 a valori frazionari inclusi. La distanza di Minkowski di ordine p è definita come

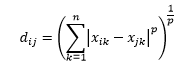
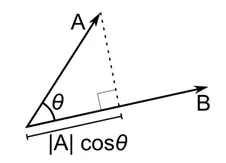
La distanza del coseno è la misura dell'angolo tra due vettori, ciascuno dei quali rappresenta due osservazioni, e formata unendo il punto dati all'origine. La distanza del coseno varia da 0 (esattamente la stessa) a 1 (nessuna connessione) e viene calcolata come

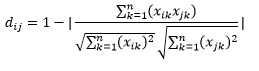
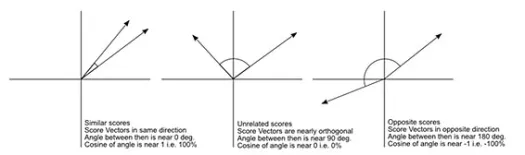
Sebbene questa sia una misura della distanza più comune quando si lavora con dati categoriali, questa può essere definita anche per il vettore numerico. Per i nostri vettori numerici, questo sarà

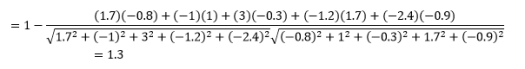
Ma attenzione agli avvertimenti...

Sapevi che sarebbe arrivato, vero? Se l'analisi fosse solo un mucchio di formule matematiche, non avremmo bisogno di persone intelligenti come te per farlo.

La prima cosa da notare è che le distanze calcolate da diverse metriche sono diverse. Potresti essere tentato di pensare che la distanza del coseno di 1,3 sia la più piccola e quindi indica che i vettori sono più vicini, ma questo non è il modo corretto di interpretare. Non è possibile confrontare le distanze tra metodi diversi e solo le distanze tra diverse coppie di osservazioni con lo stesso metodo possono essere confrontate. Le distanze hanno un significato relativo e non un significato assoluto di per sé .

Questo porta alla prossima domanda su come selezionare la giusta metrica di distanza. Sfortunatamente, non esiste una risposta vera. A seconda del tipo di dati, del contesto, del problema aziendale, dell'applicazione e del metodo di addestramento del modello, metriche diverse danno risultati diversi. Dovrai usare il giudizio, fare ipotesi o testare le prestazioni del modello per decidere la metrica giusta .

Il secondo avvertimento è quello che mi ripeto spesso sulla maledizione della dimensionalità. Nelle dimensioni superiori, le distanze non si comportano come pensiamo intuitivamente e l'analista deve essere estremamente cauto quando utilizza qualsiasi metrica.

Il terzo avvertimento riguarda la relazione tra le distanze tra tre osservazioni. Alcune metriche supportano la disuguaglianza triangolare e altre no . La disuguaglianza triangolare implica che è sempre più breve andare dal punto i al punto j direttamente, piuttosto che attraverso qualsiasi punto intermedio k. Matematicamente,

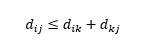
A seconda dell'applicazione, questa potrebbe essere o meno una proprietà richiesta della metrica della distanza.

Oh, un'altra cosa, "distanza" è l'opposto di "somiglianza". Maggiore è la distanza, minore è la somiglianza e viceversa. Gli algoritmi di clustering funzionano sulle distanze e gli algoritmi di raccomandazione funzionano sulla somiglianza, ma essenzialmente parlano della stessa cosa.

Quindi, come puoi trasformare il numero di distanza in un numero di somiglianza?