히스토그램을 사용한 밀도 추정

확률 밀도 함수(PDF)는 공간의 일부 영역에서 일부 연속 랜덤 변수를 관찰할 확률을 설명합니다. 1차원 확률 변수 X의 경우 PDF f(x)는 다음과 같은 속성을 따릅니다.

변수가 다음 사이의 값을 취할 확률

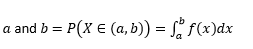
변수가 다음과 정확히 같은 값을 취할 확률

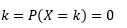
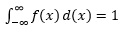
관찰 샘플에서 이러한 PDF를 추정하는 것은 기계 학습에서 일반적인 문제입니다. 이것은 샘플 관찰을 기반으로 "진정한" 분포를 추정하고 기존 또는 새로운 관찰 중 일부를 이상값으로 분류하려는 많은 이상값 감지 알고리즘에서 유용합니다. 예를 들어, 사기 적발에 관심이 있는 자동 보험사는 범퍼 교체와 같은 각 유형의 차체에 대한 청구 금액 요청을 검토하고 너무 높은 금액을 잠재적 사기로 표시할 수 있습니다. 또 다른 예로서, 아동 심리학자는 여러 아동에 걸쳐 주어진 과제를 완료하는 데 걸린 시간을 조사하고 잠재적 조사를 위해 시간이 너무 길거나 너무 짧은 아동을 표시할 수 있습니다.

이 블로그 게시물에서 우리는 각 관찰에 대한 확률을 계산하고 일반적인 또는 드문 발생 여부를 결정할 수 있도록 관찰 샘플에서 PDF를 학습하는 방법에 대해 설명합니다.

히스토그램을 사용한 밀도 추정

먼저 데모를 위해 임의의 데이터를 생성합니다.

set.seed(123)
data <- c(rnorm(200, 10, 20), rnorm(200, 60, 30), runif(200, 120, 180)) # 600 points

다음으로 그림 1과 같이 히스토그램을 사용하여 이해를 돕기 위해 시각화합니다.

# Plot 1
hist(data, breaks=50, freq=F, main="Univariate Distribution", xlab="Data Value")
# Plot 2
hist(data, breaks=20, freq=F, main="", xlab="20 Data Bins", col='red', border='red')
par(new=T)
hist(data, breaks=100, freq=F, main="Univariate Distribution", xlab=NULL, xaxt='n', yaxt='n')

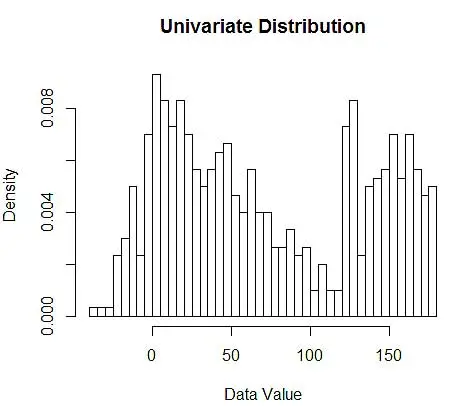
히스토그램은 데이터 시각화를 위한 차트이지만 밀도에 대한 첫 번째 추정치임을 알 수 있습니다. 보다 구체적으로, 우리는 데이터를 빈으로 나누고 밀도가 해당 빈 범위 내에서 일정하고 해당 빈에 속하는 관찰의 수와 동일한 값을 전체 관찰 수의 비율로 갖는다고 가정하여 밀도를 추정 할 수 있습니다.

따라서 추정 PDF는

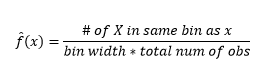
그리고 밀도 추정에 영향을 미칠 bin-width에 대한 가정을 했다는 것을 알게 됩니다. 따라서 bin-width는 histogram을 사용하는 밀도 추정 모델에 대한 매개변수 입니다. 그러나 간과된 사실은 우리 가 첫 번째 bin 의 시작 위치인 매개변수를 하나 더 사용하고 있다는 것입니다. 이것이 모든 빈에 대한 밀도 추정에 어떤 영향을 미칠 수 있는지 알 수 있습니다. 빈 너비의 영향을 확인하기 위해 그림 2는 밀도 추정치를 20-bin 및 100-bin 히스토그램으로 오버레이합니다. 더 적은/거친 빈이 평평한 밀도 추정치를 제공하는 반면 많은/더 미세한 빈이 다양한 밀도 추정치를 제공하는 원으로 둘러싸인 영역을 보십시오. 노란색 점의 경우 밀도 추정치는 두 가지 다른 모델에서 0.004에서 0.008 사이입니다.

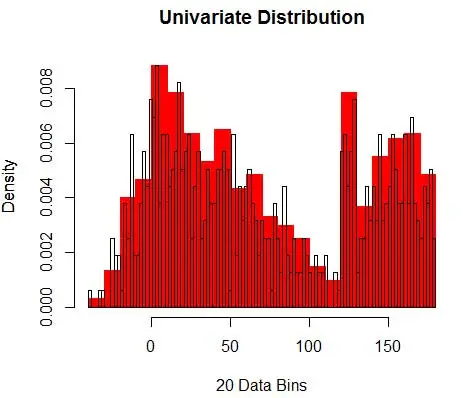
따라서 매개변수를 올바르게 선택하는 것은 밀도 추정을 올바르게 하는 데 중요합니다. 우리는 그것에 도달할 것이지만 히스토그램에 다른 문제도 있다는 점에 유의하십시오. 히스토그램을 사용한 밀도 추정치는 매우 불안정하고 불연속적 입니다. 밀도는 빈에 대해 평평하다가 빈 외부에 무한히 작은 점에 대해 갑자기 급격하게 변합니다. 이것은 실제 문제에서 잘못된 추정의 결과를 더욱 악화시킵니다.

마지막으로 설명의 편의를 위해 1차원 변수로 작업했지만 실제로는 대부분의 문제가 다차원입니다. Bin의 수가 차원의 수에 따라 기하급수적으로 증가하기 때문에 밀도를 추정하는 데 필요한 관측값의 수도 증가 합니다. 사실, 수백만 개의 관측값이 있음에도 불구하고 많은 빈이 비어 있거나 한 자릿수 관측값을 포함하고 있다는 것이 그럴듯합니다. 3차원에 각각 50개의 빈이 있으므로 채워야 하는 503=125000개의 셀이 있습니다. 이는 균일 분포, 백만 개의 관찰 훈련 데이터를 가정할 때 셀당 평균 8개의 관찰이 발생합니다.

올바른 매개변수를 선택하는 방법은 무엇입니까?

Bin-width n의 경우 관측값의 수 N의 경우 bin J의 경우 관측값의 비율은 다음과 같습니다.

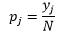
밀도 추정치는

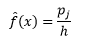
통계 이론은 f(x)가 빈의 밀도에 대한 예상 값인 반면 밀도의 분산은 다음과 같다는 것을 증명합니다.

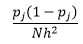
bin-width n 을 줄임으로써 더 나은 밀도 추정치를 얻을 수 있지만 너무 미세한 bin-width에 대해 직관적으로 느낄 수 있으므로 추정의 분산을 증가시킵니다. 최적의 매개변수 집합을 추정하기 위해 Leave one-out 교차 검증 기술을 사용할 수 있습니다. 우리는 하나를 제외한 모든 관측치를 사용하여 밀도를 추정할 수 있으며, 그 다음 누락된 관측치의 밀도를 계산하고 추정 오차를 측정합니다. 이것을 히스토그램에 대해 수학적으로 풀면 주어진 빈 너비에 대한 손실 함수에 대한 폐쇄형 솔루션이 제공됩니다.

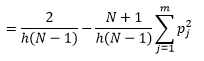
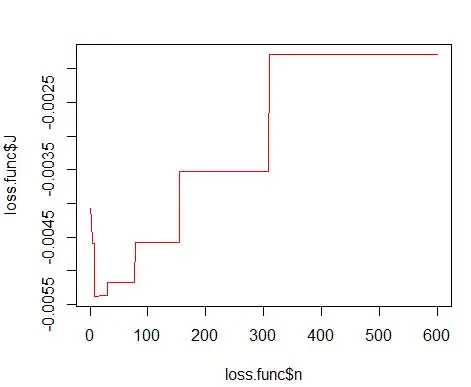
여기서 m은 빈의 수입니다. 위의 기술적인 세부 사항은 이 강의[pdf]에 있습니다. 다양한 수의 빈에 대해 이 손실 함수를 플롯할 수 있습니다(그림 3).

getLoss <- function(n.break) {
N <- 600
res <- hist(data, breaks=n.break, freq=F)
bin <- as.numeric(res$breaks)
h <- bin[2]-bin[1]
p <- res$density
p <- p * h
return ( 2/(h*(N-1)) - ( (N+1)/(h*(N-1))*sum(p*p) ) )
}
loss.func <- data.frame(n=1:600)
loss.func$J <- sapply(loss.func$n, function(x) getLoss(x))
# Plot 3
plot(loss.func$n, loss.func$J, col='red', type='l')
opt.break <- max(loss.func[loss.func$J == min(loss.func$J), 'n'])
print(opt.break)
# Plot 4
hist(data, breaks=opt.break, freq=F, main="Univariate Distribution", xlab="15 Data Bins")

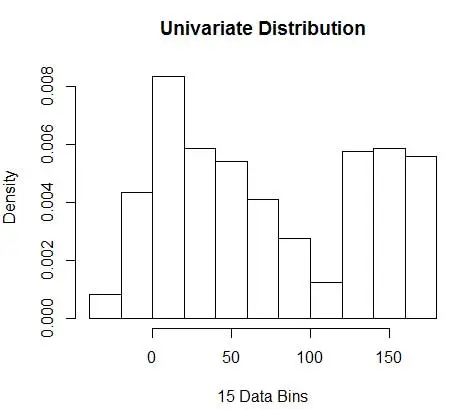
15로 최적의 숫자를 얻습니다. 실제로 8-15 사이의 모든 것이 좋습니다.

결과적으로 그림 4 아래는 밀도 값과 입도(최적의 편향-분산 트레이드오프)의 균형을 이루는 밀도 추정입니다.

이 시점에서 조금 불편하시다면 제가 함께 하겠습니다. bin의 수는 수학적으로 최적이지만 너무 조잡한 추정으로 느껴집니다. 왜 우리가 최고의 일을 했는지 직관적인 느낌이 없습니다. 그리고 시작 위치, 불연속 추정 및 차원의 저주에 대한 다른 우려도 잊지 마십시오. 실망하지 마십시오. 더 좋은 방법이 있습니다. 다음 포스트에서는 커널을 사용한 밀도 추정에 대해 이야기할 것입니다.