Przekleństwo wymiarowości
Opublikowany: 2015-07-08Czym jest Klątwa Wymiarowości?
Klątwa wymiarowości odnosi się do nieintuicyjnych właściwości danych obserwowanych podczas pracy w przestrzeni wielowymiarowej*, w szczególności związanych z użytecznością i interpretacją odległości i objętości. Jest to jeden z moich ulubionych tematów w uczeniu maszynowym i statystyce, ponieważ ma szerokie zastosowanie (nie dotyczy żadnej metody uczenia maszynowego), jest bardzo sprzeczny z intuicją, a przez to wzbudzający podziw, ma głębokie zastosowanie w każdej z technik analitycznych i ma „fajną” przerażającą nazwę jak jakaś egipska klątwa!
Dla szybkiego zrozumienia rozważmy następujący przykład: Powiedzmy, że upuściłeś monetę na 100-metrową linię. Jak ty to znalazłeś? Proste, po prostu chodź po linii i szukaj. Ale co, jeśli to 100 x 100 mkw. pole? Już teraz robi się ciężko, próbując przeszukać (z grubsza) boisko piłkarskie w poszukiwaniu jednej monety. Ale co, jeśli jest to przestrzeń 100 x 100 x 100 m3?! Wiesz, boisko do piłki nożnej ma teraz trzydzieści pięter. Powodzenia w znalezieniu monety! To w istocie „przekleństwo wymiarowości”.
Wiele metod ML wykorzystuje miary odległości
Większość metod segmentacji i klastrowania opiera się na obliczaniu odległości między obserwacjami. Dobrze znana segmentacja k-średnich przypisuje punkty do najbliższego środka. DBSCAN i klastrowanie hierarchiczne również wymagały metryk odległości. Algorytmy wykrywania wartości odstających oparte na rozkładzie i gęstości również wykorzystują odległość względem innych odległości do oznaczania wartości odstających.
Nadzorowane rozwiązania klasyfikacji, takie jak metoda k-Nearest Neighbors , również wykorzystują odległość między obserwacjami w celu przypisania klasy do nieznanej obserwacji. Metoda Support Vector Machine polega na przekształcaniu obserwacji wokół wybranych jąder na podstawie odległości między obserwacją a jądrem.
Popularna forma systemów rekomendacji obejmuje podobieństwo oparte na odległości między wektorami atrybutów użytkownika i elementu. Nawet jeśli stosowane są inne formy odległości, liczba wymiarów odgrywa rolę w projektowaniu analitycznym.
Jedną z najczęstszych metryk odległości jest metryka odległości euklidesowej, która jest po prostu liniową odległością między dwoma punktami w wielowymiarowej hiperprzestrzeni. Odległość euklidesowa dla punktu i oraz punktu j w przestrzeni n wymiarowej może być obliczona jako:
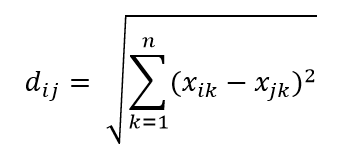
Odległość sieje spustoszenie w dużych wymiarach
Rozważ prosty proces próbkowania danych. Załóżmy, że czarna ramka na ryc. 1 to wszechświat danych z równomiernym rozkładem punktów danych na całej objętości i że chcemy próbkować 1% obserwacji zamkniętych czerwoną ramką wewnętrzną. Czarna skrzynka to hipersześcian w przestrzeni wielowymiarowej, w którym każda strona reprezentuje zakres wartości w tym wymiarze. Dla prostego trójwymiarowego przykładu na rys. 1 możemy mieć następujący zakres:
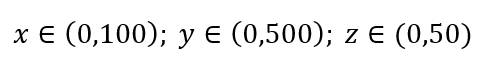
Rysunek 1: Pobieranie próbek
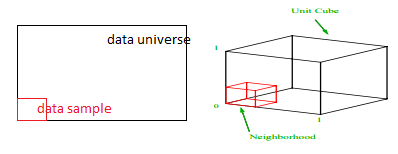
Jaka jest proporcja każdego zakresu, którą powinniśmy próbować, aby uzyskać próbkę 1%? Dla wymiarów 2-wymiarowych 10% zakresu osiągnie łącznie 1% próbkowania, więc możemy wybrać x∈(0,10) i y∈(0,50) i oczekiwać, że przechwyci 1% wszystkich obserwacji. Dzieje się tak, ponieważ 10%2=1%. Czy spodziewasz się, że ta proporcja będzie wyższa czy niższa dla trójwymiarowego?
Mimo że nasze poszukiwania zmierzają teraz w dodatkowym kierunku, proporcjonalność faktycznie wzrasta do 21,5%. I nie tylko wzrasta, ale tylko o jeden dodatkowy wymiar podwaja się! I widać, że musimy objąć prawie jedną piątą każdego wymiaru, aby uzyskać jedną setną całości! W 10-wymiarach odsetek ten wynosi 63%, aw 100-wymiarach – co nie jest rzadkością w każdym rzeczywistym uczeniu maszynowym – trzeba pobrać próbkę 95% zakresu wzdłuż każdego wymiaru, aby próbkować 1% obserwacji! Ten zdumiewający wynik ma miejsce, ponieważ w dużych wymiarach rozproszenie punktów danych staje się większe, nawet jeśli są one równomiernie rozłożone.

Ma to konsekwencje w zakresie projektowania eksperymentu i pobierania próbek. Proces staje się bardzo kosztowny obliczeniowo, nawet do tego stopnia, że próbkowanie asymptotycznie zbliża się do populacji, mimo że wielkość próby pozostaje znacznie mniejsza niż populacja.
Rozważ kolejną ogromną konsekwencję wysokiej wymiarowości. Wiele algorytmów mierzy odległość między dwoma punktami danych w celu zdefiniowania pewnego rodzaju bliskości (DBSCAN, Kernels, k-Nearest Neighbour) w odniesieniu do pewnego predefiniowanego progu odległości. W dwuwymiarach możemy sobie wyobrazić, że dwa punkty są blisko siebie, jeśli jeden znajduje się w pewnym promieniu drugiego. Rozważ lewy obraz na rys. 2. Jaki udział równomiernie rozmieszczonych punktów w czarnym kwadracie mieści się w czerwonym kółku? To jest około
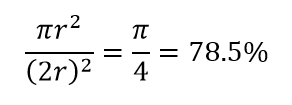
Rysunek 2 : Bliskość
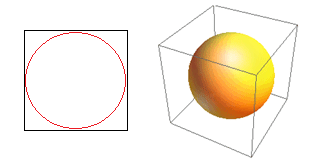
Więc jeśli zmieścisz największy możliwy okrąg wewnątrz kwadratu, pokryjesz 78% kwadratu. Jednak największa kula możliwa tylko wewnątrz sześcianu
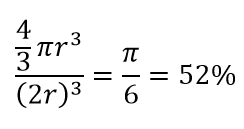
objętości. Ta objętość zmniejsza się wykładniczo do 0,24% dla zaledwie 10-wymiaru! Zasadniczo oznacza to, że w świecie wielowymiarowym każdy punkt danych znajduje się w rogach i tak naprawdę nic nie jest środkiem objętości, czyli innymi słowy, objętość środka zmniejsza się do zera, ponieważ (prawie) nie ma środka! Ma to ogromne konsekwencje związane z algorytmami klastrowania opartymi na odległości. Wszystkie odległości zaczynają wyglądać tak samo, a każda odległość większa lub mniejsza od innych jest bardziej przypadkową fluktuacją danych, a nie jakąkolwiek miarą odmienności!
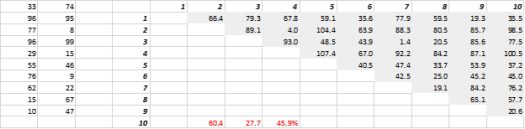
Rys. 3 przedstawia losowo wygenerowane dane 2D i odpowiadające im odległości „wszystko do wszystkich”. Współczynnik zmienności odległości, obliczony jako odchylenie standardowe podzielone przez średnią, wynosi 45,9%. Odpowiednia liczba podobnie wygenerowanych danych 5-D wynosi 26,5%, a 10-D 19,1%. Wprawdzie jest to jedna próbka, ale trend potwierdza wniosek, że w dużych wymiarach każda odległość jest mniej więcej taka sama i żadna nie jest bliska ani daleka!
Rysunek 3: Grupowanie odległości
Duży wymiar wpływa też na inne rzeczy
Oprócz odległości i objętości, wiele wymiarów stwarza inne praktyczne problemy. Wymagania dotyczące czasu wykonywania rozwiązania i pamięci systemowej często nieliniowo eskalują wraz ze wzrostem liczby wymiarów. Ze względu na wykładniczy wzrost wykonalnych rozwiązań, wiele metod optymalizacji nie może osiągnąć globalnego optymizmu i musi zadowolić się optymalizacją lokalną. Ponadto, zamiast rozwiązania w formie zamkniętej, optymalizacja musi wykorzystywać algorytmy oparte na wyszukiwaniu, takie jak opadanie gradientowe, algorytm genetyczny i symulowane wyżarzanie. Więcej wymiarów wprowadza możliwość korelacji, a estymacja parametrów może stać się trudna w podejściach regresji.
Radzenie sobie z wysokimi wymiarami
Sam w sobie będzie to osobny wpis na blogu, ale analiza korelacji, grupowanie, wartość informacyjna, współczynnik inflacji wariancji, analiza głównych komponentów to tylko niektóre ze sposobów, w jakie można zmniejszyć liczbę wymiarów.
* Liczba zmiennych, obserwacji lub cech, z których składa się punkt danych, nazywana jest wymiarem danych. Na przykład dowolny punkt w przestrzeni można przedstawić za pomocą 3 współrzędnych długości, szerokości i wysokości oraz ma 3 wymiary
