Szacowanie gęstości za pomocą histogramów

Funkcje gęstości prawdopodobieństwa (PDF) opisują prawdopodobieństwo obserwowania pewnej ciągłej zmiennej losowej w pewnym obszarze przestrzeni. Przypomnij sobie, że dla jednowymiarowej zmiennej losowej X, PDF f(x) ma właściwości, które

Prawdopodobieństwo, że zmienna przyjmuje wartości między

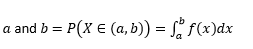
Prawdopodobieństwo, że zmienna przyjmuje wartości dokładnie równe

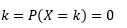
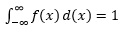
Szacowanie takiego pliku PDF na podstawie próbki obserwacji jest częstym problemem w uczeniu maszynowym. Jest to przydatne w wielu algorytmach wykrywania wartości odstających, w których staramy się oszacować „prawdziwy” rozkład na podstawie obserwacji próbki, a następnie klasyfikować niektóre z istniejących lub nowych obserwacji jako odstające lub nie. Na przykład, autoubezpieczyciel zainteresowany wykryciem oszustwa może zbadać żądanie kwoty roszczenia dla każdego rodzaju nadwozia, powiedzmy, wymiany zderzaka, i oznaczyć jako potencjalne oszustwo każdą kwotę, która jest zbyt wysoka. Inny przykład: psycholog dziecięcy może zbadać czas potrzebny na wykonanie danego zadania u różnych dzieci i oznaczyć te dzieci, którym potencjalne badanie trwa zbyt długo lub zbyt krótko.

W tym poście na blogu omawiamy, w jaki sposób możemy nauczyć się pliku PDF z próbki obserwacji , abyśmy mogli obliczyć prawdopodobieństwo dla każdej obserwacji i zdecydować, czy występuje ona często, czy rzadko.

Szacowanie gęstości za pomocą histogramu

Najpierw generujemy losowe dane do demonstracji.

set.seed(123)
data <- c(rnorm(200, 10, 20), rnorm(200, 60, 30), runif(200, 120, 180)) # 600 points

Następnie wizualizujemy je dla naszego zrozumienia za pomocą histogramu, jak na rysunku 1.

# Plot 1
hist(data, breaks=50, freq=F, main="Univariate Distribution", xlab="Data Value")
# Plot 2
hist(data, breaks=20, freq=F, main="", xlab="20 Data Bins", col='red', border='red')
par(new=T)
hist(data, breaks=100, freq=F, main="Univariate Distribution", xlab=NULL, xaxt='n', yaxt='n')

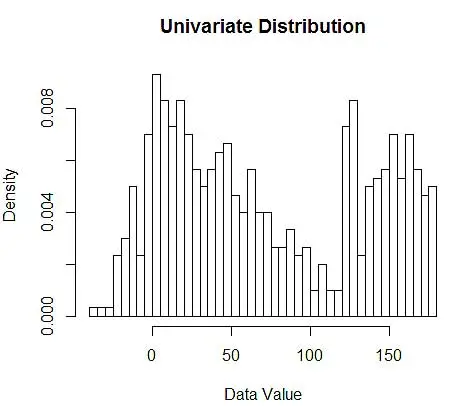
Chociaż histogramy to wykresy służące do wizualizacji danych, można również zauważyć, że stanowią one nasze pierwsze oszacowanie gęstości. Mówiąc dokładniej, możemy oszacować gęstość, dzieląc dane na przedziały i zakładając, że gęstość jest stała w tym zakresie przedziałów i ma wartość równą liczbie obserwacji znajdujących się w tym przedziale jako proporcji całkowitej liczby obserwacji

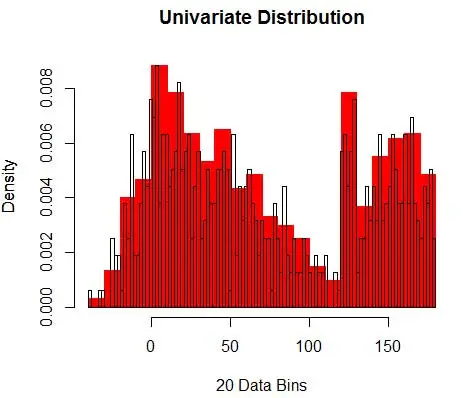
Dlatego szacowany plik PDF to

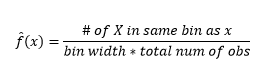
I zdajesz sobie sprawę, że przyjąłeś założenie dotyczące szerokości przedziału, które wpłynie na oszacowanie gęstości. Stąd szerokość bin jest parametrem modelu szacowania gęstości za pomocą histogramu . Jednak przeoczonym faktem jest to, że pracujemy również z jeszcze jednym parametrem – jest to pozycja początkowa pierwszego pojemnika . Możesz zobaczyć, jak może to wpłynąć na szacowanie gęstości dla wszystkich pojemników. Aby zobaczyć wpływ szerokości przedziału, Rysunek 2 nakłada oszacowania gęstości z histogramami 20 i 100 przedziałów. Spójrz na region otoczony, gdzie mniej/grubsze kosze dają oszacowanie płaskiej gęstości, podczas gdy wiele/drobniejszych koszy daje oszacowanie różnej gęstości. W przypadku żółtego punktu oszacowania gęstości będą wynosić od 0,004 do 0,008 na podstawie dwóch różnych modeli.

W związku z tym właściwy dobór parametrów ma kluczowe znaczenie dla prawidłowego oszacowania gęstości. Dojdziemy do tego, ale zwróć uwagę, że są też inne problemy z histogramami. Szacunki gęstości za pomocą histogramów są dość niestabilne i nieciągłe . Gęstość jest płaska dla kosza, a następnie nagle zmienia się drastycznie dla punktu nieskończenie małego poza koszem. To sprawia, że ​​konsekwencje błędnego oszacowania są jeszcze gorsze w przypadku problemów praktycznych.

Na koniec pracowaliśmy ze zmienną jednowymiarową, aby ułatwić ilustrację, ale w praktyce większość problemów jest wielowymiarowa. Ponieważ liczba pojemników rośnie wykładniczo wraz z liczbą wymiarów, rośnie również liczba obserwacji wymaganych do oszacowania gęstości . W rzeczywistości jest prawdopodobne, że pomimo milionów obserwacji, wiele pojemników pozostaje pustych lub zawiera obserwacje jednocyfrowe. Z zaledwie 50 pojemnikami każdy w zaledwie 3 wymiarach, mamy 503=125000 komórek, które należy wypełnić. Daje to średnio 8 obserwacji na komórkę, zakładając równomierny rozkład, milion danych treningowych obserwacji.

Jak dobrać odpowiednie parametry?

Dla szerokości binu n liczba obserwacji N dla bin J proporcja obserwacji wynosi

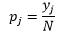
a oszacowanie gęstości to

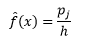
Teoria statystyczna dowodzi, że o ile f(x) jest oczekiwaną wartością gęstości w koszu, o tyle wariancja gęstości wynosi

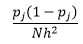
Chociaż możemy uzyskać lepsze oszacowanie gęstości, zmniejszając szerokość przedziału n , zwiększamy wariancję oszacowania, ponieważ intuicyjnie możemy wyczuć zbyt małą szerokość przedziału. Do oszacowania optymalnego zestawu parametrów możemy zastosować technikę walidacji krzyżowej typu „jeden-out”. Możemy oszacować gęstość za pomocą wszystkich obserwacji z wyjątkiem jednej, a następnie obliczyć gęstość tej obserwacji, pomijając obserwację i zmierzyć błąd w estymacji. Rozwiązanie tego matematycznie dla histogramów daje rozwiązanie w postaci zamkniętej dla funkcji straty dla danej szerokości kosza.

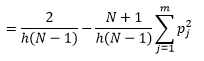
gdzie m to liczba pojemników. Szczegóły techniczne powyższego znajdują się w tym wykładzie [pdf] . Możemy wykreślić tę funkcję straty dla różnej liczby pojemników (rysunek 3)

getLoss <- function(n.break) {
N <- 600
res <- hist(data, breaks=n.break, freq=F)
bin <- as.numeric(res$breaks)
h <- bin[2]-bin[1]
p <- res$density
p <- p * h
return ( 2/(h*(N-1)) - ( (N+1)/(h*(N-1))*sum(p*p) ) )
}
loss.func <- data.frame(n=1:600)
loss.func$J <- sapply(loss.func$n, function(x) getLoss(x))
# Plot 3
plot(loss.func$n, loss.func$J, col='red', type='l')
opt.break <- max(loss.func[loss.func$J == min(loss.func$J), 'n'])
print(opt.break)
# Plot 4
hist(data, breaks=opt.break, freq=F, main="Univariate Distribution", xlab="15 Data Bins")

i uzyskaj optymalną liczbę jako 15. Właściwie wszystko od 8-15 jest w porządku.

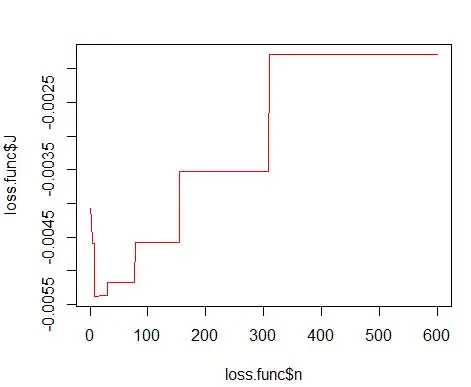
W związku z tym poniżej Rysunek 4 przedstawia oszacowanie gęstości, które równoważy wartości gęstości oraz ziarnistość (z optymalnym kompromisem między odchyleniem a wariancją).

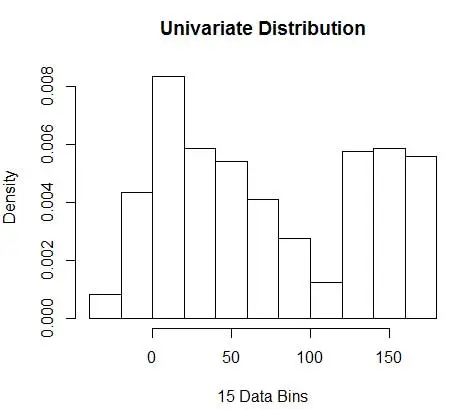
Jeśli w tym momencie czujesz się trochę nieswojo, jestem z tobą. Mimo że liczba pojemników jest matematycznie optymalna, wydaje się, że oszacowanie jest zbyt zgrubne. Nie ma intuicyjnego wyczucia, dlaczego wykonaliśmy najlepszą pracę. I nie zapominajmy o innych obawach związanych z pozycją początkową, nieciągłą estymacją i przekleństwem wymiarowości. Nie rozpaczaj, jest lepszy sposób. W następnym poście porozmawiamy o szacowaniu gęstości za pomocą jąder.