Pomiar odległości w nadprzestrzeni

Każdy, kto pobieżnie zaznajomił się z technikami analitycznymi, zauważyłby wiele algorytmów, które w celu ich zastosowania opierają się na odległościach między punktami danych. Każda obserwacja lub instancja danych jest zwykle reprezentowana jako wielowymiarowy wektor, a dane wejściowe do algorytmu wymagają odległości między każdą parą takich obserwacji.

Metoda obliczania odległości zależy od rodzaju danych – liczbowe, kategoryczne lub mieszane. Niektóre algorytmy dotyczą tylko jednej klasy obserwacji, podczas gdy inne działają na wielu. W tym poście omówimy miary odległości, które działają na danych liczbowych. Być może istnieje więcej sposobów mierzenia odległości w wielowymiarowej hiperprzestrzeni niż te, które można opisać w jednym poście na blogu, i zawsze można wymyślić nowsze sposoby, ale przyjrzymy się niektórym typowym miernikom odległości i ich relatywnym zaletom.

Na potrzeby dalszej części wpisu na blogu sugerujemy

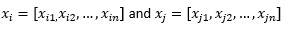
odnosić się do dwóch obserwacji lub wektorów danych.

Najpierw przygotuj dane…

Zanim przejrzymy różne metryki odległości, musimy przygotować dane:

Transformacja do wektora numerycznego

W przypadku obserwacji mieszanej, która zawiera zarówno wymiar liczbowy, jak i kategoryczny, pierwszym krokiem jest faktyczne przekształcenie wymiaru kategorycznego na wymiar(y) liczbowe. Wymiar kategoryczny z trzema potencjalnymi wartościami można przekształcić w dwa lub trzy wymiary liczbowe z wartościami binarnymi. Ponieważ ta zmienna kategorialna z konieczności przyjmuje jedną z trzech wartości, jeden z trzech wymiarów liczbowych będzie doskonale skorelowany z pozostałymi dwoma. Może to być w porządku lub nie, w zależności od aplikacji.

Jeśli obserwacja jest czysto kategoryczna, na przykład ciąg tekstowy (zdania o różnej długości) lub sekwencja genomu (sekwencje o stałej długości), wówczas można bezpośrednio zastosować jakąś specjalną metrykę odległości bez przekształcania danych na format liczbowy. Omówimy te algorytmy w następnym poście.

Normalizacja

W zależności od przypadku użycia możesz chcieć znormalizować każdy wymiar w tej samej skali, aby odległość wzdłuż dowolnego wymiaru nie wpływała nadmiernie na ogólną odległość między obserwacjami. To samo zostało omówione w algorytmie k-średnich. Możliwe są dwa rodzaje normalizacji:

Normalizacja zakresu (ponowne skalowanie) normalizuje dane tak, aby mieściły się w zakresie 0-1, odejmując minimalną wartość z każdego wymiaru, a następnie dzieląc przez zakres wartości w tym wymiarze.

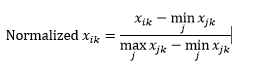
Pierwszy problem z normalizacją zakresu polega na tym, że niewidoczna wartość może zostać znormalizowana poza zakres 0-1. Chociaż generalnie nie jest to problemem dla większości metryk odległości, ale jeśli algorytm nie może obsłużyć wartości ujemnych, może to stanowić problem. Drugim problemem jest to, że jest to w dużym stopniu zależne od wartości odstających. Jeśli jedna obserwacja ma bardzo ekstremalną (wysoką lub niską) wartość dla wymiaru, znormalizowana wartość dla tego wymiaru dla innych obserwacji zostanie zebrana razem i straci swoją moc dyskryminacyjną.

Normalizacja standardowa (skalowanie z) normalizuje wymiar tak, aby miał 0 średniej i 1 odchylenie standardowe, odejmując średnią od tego wymiaru każdej obserwacji, a następnie dzieląc przez odchylenie standardowe wartości tego wymiaru we wszystkich obserwacjach.

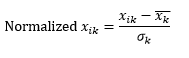
To na ogół utrzymuje dane w zakresie od -5 do +5, z grubsza i pozwala uniknąć wpływu wartości ekstremalnych.

Przeprowadziliśmy symulację skalowania z dwóch obserwacji. Symulacja, ponieważ naprawdę potrzebujemy znacznie więcej niż dwóch obserwacji, aby obliczyć średnią i odchylenie standardowe każdego wymiaru, i założyliśmy tutaj obie te liczby dla każdego wymiaru.

Następnie oblicz odległość…

Odległość euklidesowa – czyli odległość „w linii prostej” – to najkrótsza odległość w wielowymiarowej hiperprzestrzeni między dwoma punktami. Znasz to w płaszczyźnie 2D lub przestrzeni 3D (to jest linia), ale podobna koncepcja rozciąga się na wyższe wymiary. Odległość euklidesowa między wektorami w przestrzeni n-wymiarowej jest obliczana jako

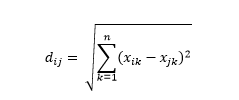
W przypadku przekształconych przykładów wektorów danych jest to

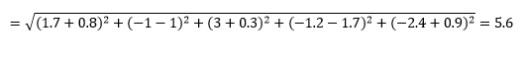
Jest to najczęstsza metryka i często bardzo odpowiednia dla większości zastosowań. Wariantem tego jest kwadratowa odległość euklidesowa, która jest po prostu sumą kwadratów różnic.

Odległość Manhattanu – nazwana ze względu na siatkę Wschód-Zachód-Północ-Południe, przypominającą strukturę ulic Manhattanu w Nowym Jorku – to odległość między dwoma punktami podczas ruchu równoległego do osi.

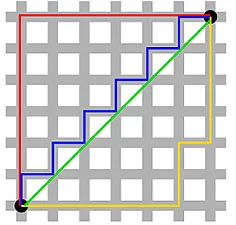
Odległość od Manhattanu
Odległość euklidesowa

Jest to obliczane jako

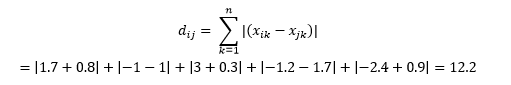
Może to być przydatne w niektórych aplikacjach, w których odległość jest używana w prawdziwym, fizycznym sensie, a nie w sensie „odmienności” uczenia maszynowego. Na przykład, jeśli musisz obliczyć odległość pokonaną przez wóz strażacki, aby dotrzeć do punktu, użycie tego jest bardziej praktyczne.

Odległość Canberry jest ważonym wariantem odległości Manhattan i jest obliczana jako

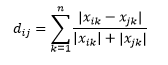
Odległość L-norm jest rozszerzeniem powyżej dwóch – lub można powiedzieć, że powyższe dwa są konkretnymi przypadkami odległości L-normy – i jest zdefiniowana jako

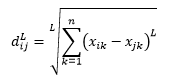
gdzie L jest dodatnią liczbą całkowitą. Nie natknąłem się na żadne przypadki, w których musiałbym to wykorzystać, ale nadal dobrze jest wiedzieć o tej możliwości. Na przykład odległość 3 norm będzie

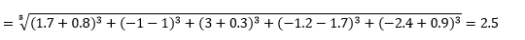
Zwróć uwagę, że L powinno generalnie być parzystą liczbą całkowitą, ponieważ nie chcemy, aby dodatnie lub ujemne składki na odległość były anulowane.

Odległość Minkowskiego jest uogólnieniem odległości L-norm, gdzie L może przyjąć dowolną wartość od 0 do wartości ułamkowych. Odległość Minkowskiego rzędu p jest określona jako

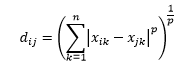
Odległość cosinus jest miarą kąta między dwoma wektorami, z których każdy reprezentuje dwie obserwacje, i jest utworzona przez połączenie punktu danych z początkiem. Odległość cosinusa wynosi od 0 (dokładnie taka sama) do 1 (brak połączenia) i jest obliczana jako

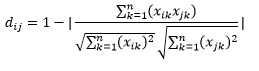
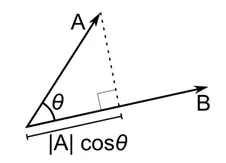
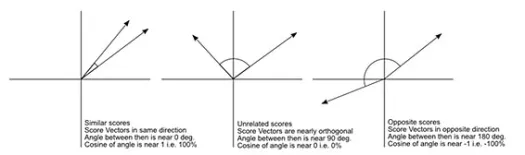
Chociaż jest to bardziej powszechna miara odległości podczas pracy z danymi kategorialnymi, można ją również zdefiniować dla wektora numerycznego. Dla naszych wektorów numerycznych będzie to

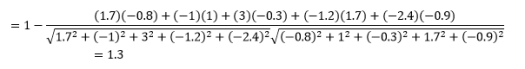
Ale pamiętaj o zastrzeżeniach…

Wiedziałeś, że to nadchodzi, prawda? Gdyby analityka była tylko zbiorem formuł matematycznych, nie potrzebowalibyśmy do tego mądrych ludzi takich jak ty.

Pierwszą rzeczą, na którą należy zwrócić uwagę, jest to, że odległości obliczane przez różne metryki są różne. Możesz pokusić się o stwierdzenie, że odległość cosinusa równa 1,3 jest najmniejsza, a zatem wskazuje, że wektory są najbliższe, ale nie jest to właściwy sposób interpretacji. Odległości między różnymi metodami nie mogą być porównywane i można porównywać tylko odległości między różnymi parami obserwacji w ramach tej samej metody. Odległości mają znaczenie względne i same w sobie nie mają znaczenia absolutnego .

To prowadzi do kolejnego pytania, jak wybrać odpowiednią metrykę odległości. Niestety nie ma prawdziwej odpowiedzi. W zależności od typu danych, kontekstu, problemu biznesowego, aplikacji i metody uczenia modelu, różne metryki dają różne wyniki. Będziesz musiał użyć osądu, poczynić założenia lub przetestować wydajność modelu, aby wybrać odpowiednią metrykę .

Drugie zastrzeżenie to moje często powtarzane o przekleństwie wymiarowości. W wyższych wymiarach odległości nie zachowują się w sposób, w jaki intuicyjnie myślimy, że zachowują się , a analityk musi być niezwykle ostrożny, gdy używa dowolnej metryki.

Trzecie zastrzeżenie dotyczy relacji między odległościami między trzema obserwacjami. Niektóre metryki obsługują nierówność trójkątów, a inne nie . Nierówność trójkąta implikuje, że zawsze najkrótsze jest przejście bezpośrednio z punktu i do punktu j, a nie przez jakikolwiek punkt pośredni k. Matematycznie,

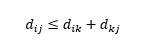
W zależności od aplikacji może to być lub nie być wymagana właściwość metryki odległości.

Och, jeszcze jedno, „odległość” jest przeciwieństwem „podobieństwa”. Większa odległość, mniejsze podobieństwo i odwrotnie. Algorytmy klastrowania działają na odległościach, a algorytmy rekomendacji działają na podobieństwie, ale zasadniczo mówią o tym samym.

Jak więc przekształcić liczbę odległości na liczbę podobieństwa?