Maldição da Dimensionalidade
Publicados: 2015-07-08O que é Maldição da Dimensionalidade
Curse of Dimensionality refere-se a propriedades não intuitivas de dados observados ao trabalhar em espaço de alta dimensão*, especificamente relacionadas à usabilidade e interpretação de distâncias e volumes. Este é um dos meus tópicos favoritos em Aprendizado de Máquina e Estatística, pois tem aplicações amplas (não específicas para nenhum método de aprendizado de máquina), é muito contra-intuitivo e, portanto, inspirador, tem aplicação profunda para qualquer uma das técnicas de análise e tem nome assustador 'legal' como alguma maldição egípcia!
Para uma compreensão rápida, considere este exemplo: digamos, você deixou cair uma moeda em uma linha de 100 metros. Como você o encontra? Simples, basta andar na linha e pesquisar. Mas e se for 100 x 100 m². campo? Já está ficando difícil, tentar procurar um campo de futebol (aproximadamente) por uma única moeda. Mas e se for 100 x 100 x 100 m³ de espaço?! Você sabe, o campo de futebol agora tem trinta andares de altura. Boa sorte para encontrar uma moeda lá! Isso, em essência, é “maldição da dimensionalidade”.
Muitos métodos de ML usam a Medida de distância
A maioria dos métodos de segmentação e agrupamento depende de distâncias computacionais entre observações. A bem conhecida segmentação k-Means atribui pontos ao centro mais próximo . O agrupamento DBSCAN e hierárquico também exigia métricas de distância. Os algoritmos de detecção de outliers baseados em distribuição e densidade também fazem uso da distância relativa a outras distâncias para marcar outliers.
As soluções de classificação supervisionada, como o método k-Nearest Neighbors , também usam a distância entre as observações para atribuir classe à observação desconhecida. O método Support Vector Machine envolve a transformação de observações em torno de Kernels selecionados com base na distância entre a observação e o kernel.
A forma comum de sistemas de recomendação envolve similaridade baseada em distância entre vetores de atributos de usuário e item. Mesmo quando outras formas de distâncias são usadas, o número de dimensões desempenha um papel no projeto analítico.
Uma das métricas de distância mais comuns é a métrica de Distância Euclidiana, que é simplesmente a distância linear entre dois pontos no hiperespaço multidimensional. A distância euclidiana para o ponto i e o ponto j no espaço n dimensional pode ser calculada como:
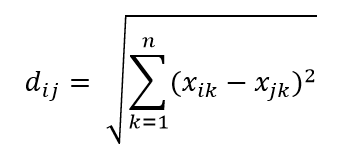
A distância causa estragos em alta dimensão
Considere um processo simples de amostragem de dados. Suponha que a caixa preta externa na Fig. 1 seja um universo de dados com distribuição uniforme de pontos de dados em todo o volume e que queremos amostrar 1% das observações delimitadas pela caixa interna vermelha. A caixa preta é um hipercubo no espaço multidimensional com cada lado representando o intervalo de valor nessa dimensão. Para um exemplo tridimensional simples na Fig. 1, podemos ter o seguinte intervalo:
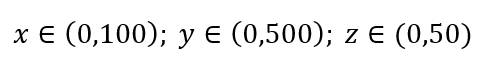
Figura 1: Amostragem
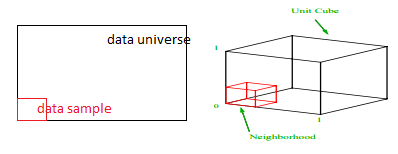
Qual é a proporção de cada intervalo que devemos amostrar para obter essa amostra de 1%? Para 2-dimensões, 10% do alcance atingirá 1% de amostragem geral, então podemos selecionar x∈(0,10) e y∈(0,50) e esperar capturar 1% de todas as observações. Isso ocorre porque 10%2=1%. Você espera que essa proporção seja maior ou menor para 3 dimensões?
Mesmo que nossa busca esteja agora em direção adicional, a proporcional na verdade aumenta para 21,5%. E não só aumenta, por apenas uma dimensão adicional, dobra! E você pode ver que temos que cobrir quase um quinto de cada dimensão apenas para obter um centésimo do total! Em 10 dimensões, essa proporção é de 63% e em 100 dimensões – o que não é um número incomum de dimensões em qualquer aprendizado de máquina da vida real – é preciso amostrar 95% do intervalo ao longo de cada dimensão para amostrar 1% das observações! Esse resultado alucinante acontece porque, em dimensões altas, a dispersão dos pontos de dados se torna maior, mesmo que eles sejam distribuídos uniformemente.

Isso tem consequências em termos de desenho de experimento e amostragem. O processo se torna muito caro computacionalmente, mesmo na medida em que a amostragem se aproxima assintoticamente da população, apesar do tamanho da amostra permanecer muito menor que a população.
Considere outra grande consequência da alta dimensionalidade. Muitos algoritmos medem a distância entre dois pontos de dados para definir algum tipo de proximidade (DBSCAN, Kernels, k-Nearest Neighbour) em referência a algum limite de distância predefinido. Em 2-dimensões, podemos imaginar que dois pontos estão próximos se um cair dentro de certo raio de outro. Considere a imagem da esquerda na Fig. 2. Qual é a proporção de pontos uniformemente espaçados dentro do quadrado preto dentro do círculo vermelho? Isso é sobre
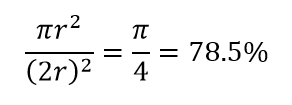
Figura 2: Proximidade
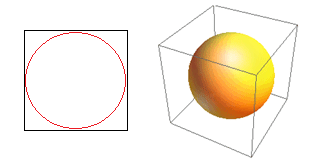
Então, se você encaixar o maior círculo possível dentro do quadrado, você cobre 78% do quadrado. No entanto, a maior esfera possível dentro do cubo cobre apenas
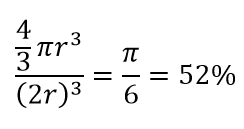
do volume. Este volume reduz exponencialmente para 0,24% para apenas 10 dimensões! O que significa essencialmente que no mundo de alta dimensão cada ponto de dados está nos cantos e nada é realmente o centro de volume, ou em outras palavras, o volume do centro se reduz a nada porque não há (quase) nenhum centro! Isso tem enormes consequências dos algoritmos de agrupamento baseados em distância. Todas as distâncias começam a parecer iguais e qualquer distância maior ou menor do que a outra é mais flutuação aleatória nos dados do que qualquer medida de dissimilaridade!
A Fig. 3 mostra dados 2-D gerados aleatoriamente e as distâncias de todos para todos correspondentes. O Coeficiente de Variação da distância, calculado como Desvio Padrão dividido pela Média, é de 45,9%. O número correspondente de dados 5-D gerados de forma semelhante é 26,5% e para 10-D é 19,1%. É certo que esta é uma amostra, mas a tendência apoia a conclusão de que em dimensões altas todas as distâncias são aproximadamente iguais, e nenhuma está perto ou longe!
Figura 3: Agrupamento de distância
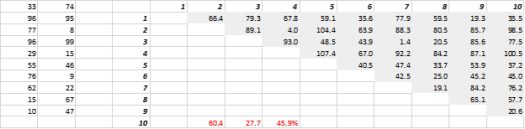
Alta dimensão afeta outras coisas também
Além de distâncias e volumes, o número de dimensões cria outros problemas práticos. O tempo de execução da solução e os requisitos de memória do sistema geralmente aumentam de forma não linear com o aumento do número de dimensões. Devido ao aumento exponencial de soluções viáveis, muitos métodos de otimização não podem alcançar ótimos globais e precisam se contentar com ótimos locais. Além disso, em vez de uma solução de forma fechada, a otimização deve usar algoritmos baseados em pesquisa, como gradiente descendente, algoritmo genético e recozimento simulado. Mais dimensões introduzem a possibilidade de correlação e a estimativa de parâmetros pode se tornar difícil em abordagens de regressão.
Lidando com alta dimensão
Esta será uma postagem de blog separada em si, mas a análise de correlação, agrupamento, valor da informação, fator de inflação de variância, análise de componentes principais são algumas das maneiras pelas quais o número de dimensões pode ser reduzido.
* O número de variáveis, observações ou características de que um ponto de dados é composto é chamado de dimensão de dados. Por exemplo, qualquer ponto no espaço pode ser representado usando 3 coordenadas de comprimento, largura e altura, e tem 3 dimensões
