Estimativa de densidade usando histogramas

As Funções de Densidade de Probabilidade (PDFs) descrevem a probabilidade de observar alguma variável aleatória contínua em alguma região do espaço. Para uma variável aleatória dimensional X, lembre-se de que PDF f(x) segue as propriedades que

Probabilidade de que a variável assuma valores entre

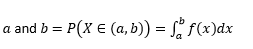
Probabilidade de que a variável receba valores exatamente iguais a

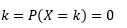
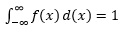
Estimar tal PDF a partir de uma amostra de observações é um problema comum em Machine Learning. Isso é útil em muitos algoritmos de detecção de valores discrepantes, nos quais procuramos estimar a distribuição “verdadeira” com base em observações de amostra e, em seguida, classificamos algumas das observações existentes ou novas como atípicas ou não. Por exemplo, uma seguradora de automóveis interessada em detectar fraudes pode examinar a solicitação de valor de sinistro para cada tipo de carroceria, digamos, substituição de pára-choques, e marcar para fraude em potencial qualquer valor que seja muito alto. Por meio de outro exemplo, um psicólogo infantil pode examinar o tempo gasto para concluir uma determinada tarefa em diferentes crianças e marcar aquelas crianças que demoram muito ou muito pouco tempo para uma investigação potencial.

Nesta postagem do blog, discutimos como podemos aprender o PDF a partir de uma amostra de observações , para que possamos calcular a probabilidade de cada observação e decidir se é uma ocorrência comum ou rara.

Estimativa de densidade usando histograma

Primeiro geramos alguns dados aleatórios para demonstração.

set.seed(123)
data <- c(rnorm(200, 10, 20), rnorm(200, 60, 30), runif(200, 120, 180)) # 600 points

Em seguida, visualizá-los para nossa compreensão, usando histograma, como na Figura 1.

# Plot 1
hist(data, breaks=50, freq=F, main="Univariate Distribution", xlab="Data Value")
# Plot 2
hist(data, breaks=20, freq=F, main="", xlab="20 Data Bins", col='red', border='red')
par(new=T)
hist(data, breaks=100, freq=F, main="Univariate Distribution", xlab=NULL, xaxt='n', yaxt='n')

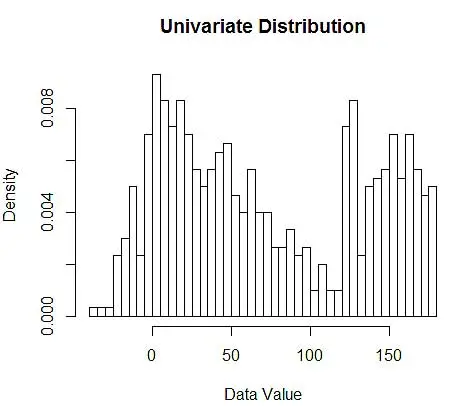
Embora os histogramas sejam gráficos para visualização de dados, você também pode ver que eles são nossa primeira estimativa de densidade. Mais especificamente, podemos estimar a densidade dividindo os dados em compartimentos e assumindo que a densidade é constante dentro desse intervalo de compartimento e tem valor igual ao número de observações que caem nesse compartimento como proporção do número total de observações

Assim, o PDF estimado é

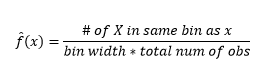
E você percebe que fez uma suposição sobre a largura do compartimento, o que afetará a estimativa de densidade. Portanto , bin-width é um parâmetro para o modelo de estimativa de densidade usando histograma . No entanto, o fato esquecido é que também estamos trabalhando com mais um parâmetro – que é a posição inicial do primeiro bin . Você pode ver como isso pode afetar as estimativas de densidade para todos os compartimentos. Para ver o impacto da largura do compartimento, a Figura 2 sobrepõe as estimativas de densidade com histogramas de 20 e 100 compartimentos. Observe a região circundada, onde menos/mais grossos fornecem uma estimativa de densidade plana, enquanto muitos/mais finos fornecem uma estimativa de densidade variável. Para o ponto amarelo, as estimativas de densidade variam de 0,004 a 0,008 a partir de dois modelos diferentes.

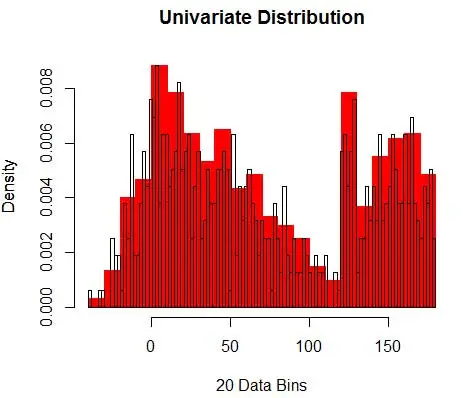
Assim, selecionar os parâmetros corretos é crucial para obter a estimativa de densidade correta. Chegaremos a isso, mas observe que também existem outros problemas com histogramas. As estimativas de densidade usando histogramas são bastante irregulares e descontínuas . A densidade é plana para uma caixa e, de repente, muda drasticamente para um ponto infinitesimalmente fora da caixa. Isso torna a consequência da estimativa errada ainda pior para problemas práticos.

Por fim, trabalhamos com variáveis ​​unidimensionais para facilitar a ilustração, mas na prática a maioria dos problemas são multidimensionais. Como o número de caixas cresce exponencialmente com o número de dimensões, o número de observações necessárias para estimar a densidade também cresce . De fato, é plausível que, apesar de ter milhões de observações, muitas caixas permaneçam vazias ou contenham observações de um dígito. Com apenas 50 compartimentos cada em apenas 3 dimensões, temos 503=125.000 células que precisam ser preenchidas. Isso é uma média de 8 observações por célula, assumindo distribuição uniforme, um milhão de dados de treinamento de observação.

Como selecionar os parâmetros corretos?

Para a largura do compartimento n número de observações N para o compartimento J, a proporção de observações é

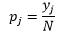
e a estimativa de densidade é

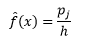
A teoria estatística prova que enquanto f(x) é o valor esperado da densidade no compartimento, a variância da densidade é

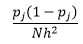
Embora possamos obter uma melhor estimativa de densidade reduzindo a largura do compartimento n , aumentamos a variância da estimativa, pois podemos intuitivamente sentir que a largura do compartimento é muito fina. Podemos usar a técnica de validação cruzada leave one-out para estimar o conjunto ótimo de parâmetros. Podemos estimar a densidade usando todas as observações, exceto uma, e então calcular a densidade dessa observação omitida e medir o erro na estimativa. Resolver isso matematicamente para histogramas fornece uma solução de forma fechada para a função de perda para uma determinada largura do compartimento.

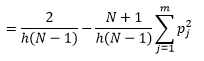
onde m é o número de compartimentos. Os detalhes técnicos acima estão nesta palestra [pdf] . Podemos plotar essa função de perda para vários números de caixas (Figura 3)

getLoss <- function(n.break) {
N <- 600
res <- hist(data, breaks=n.break, freq=F)
bin <- as.numeric(res$breaks)
h <- bin[2]-bin[1]
p <- res$density
p <- p * h
return ( 2/(h*(N-1)) - ( (N+1)/(h*(N-1))*sum(p*p) ) )
}
loss.func <- data.frame(n=1:600)
loss.func$J <- sapply(loss.func$n, function(x) getLoss(x))
# Plot 3
plot(loss.func$n, loss.func$J, col='red', type='l')
opt.break <- max(loss.func[loss.func$J == min(loss.func$J), 'n'])
print(opt.break)
# Plot 4
hist(data, breaks=opt.break, freq=F, main="Univariate Distribution", xlab="15 Data Bins")

e obtenha o número ideal como 15. Na verdade, qualquer coisa de 8 a 15 está bem.

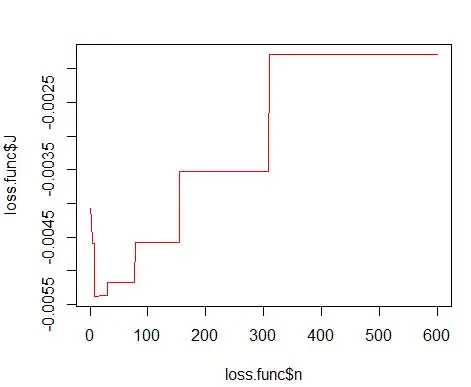
Consequentemente, abaixo da Figura 4 está a estimativa de densidade que equilibra os valores de densidade bem como a granularidade (com compensação ótima de variância de viés).

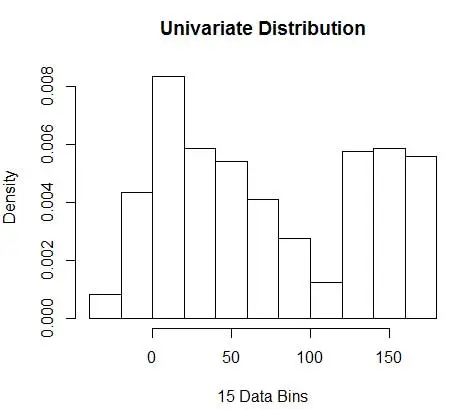
Se você se sente um pouco desconfortável neste momento, então estou com você. Mesmo assim, o número de caixas é matematicamente ideal, parece uma estimativa muito grosseira. Não há um sentimento intuitivo de por que fizemos o melhor trabalho. E para não esquecer outras preocupações sobre posição inicial, estimativa descontínua e maldição de dimensionalidade. Não se desespere, há uma maneira melhor. No próximo post falaremos sobre Estimativa de Densidade usando Kernels.