Medindo a distância no hiperespaço

Qualquer pessoa superficialmente familiarizada com técnicas analíticas teria notado muitos algoritmos que dependem de distâncias entre pontos de dados para sua aplicação. Cada observação, ou instância de dados, geralmente é representada como um vetor multidimensional, e a entrada para o algoritmo requer distâncias entre cada par de tais observações.

O método de cálculo de distância depende do tipo de dados – numérico, categórico ou misto. Alguns dos algoritmos se aplicam a apenas uma classe de observações, enquanto outros trabalham em várias. Neste post, discutiremos medidas de distância que funcionam em dados numéricos. Talvez existam mais maneiras de medir a distância no hiperespaço multidimensional do que aquelas que podem ser abordadas em uma única postagem no blog, e sempre é possível inventar maneiras mais novas, mas analisamos algumas das métricas comuns de distância e seus méritos relativos.

Para fins do restante da postagem do blog, sugerimos

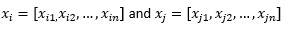
para se referir a duas observações ou vetores de dados.

Primeiro prepare os dados…

Antes de revisarmos as diferentes métricas de distância, precisamos preparar os dados:

Transformação em vetor numérico

Para observação mista, que contém dimensões numéricas e categóricas, o primeiro passo é realmente transformar a dimensão categórica em dimensão(ões) numérica(s). Uma dimensão categórica com três valores potenciais pode ser transformada em duas ou três dimensões numéricas com valores binários. Como essa variável categórica necessariamente assume um dos três valores, uma das três dimensões numéricas estará perfeitamente correlacionada com as outras duas. Isso pode ou não ser aceitável dependendo da sua aplicação.

Se a observação for puramente categórica, como sequência de texto (frases de comprimento variável) ou sequência do genoma (sequências de comprimento fixo), então alguma métrica de distância especial pode ser aplicada diretamente sem transformar os dados em formato numérico. Discutiremos esses algoritmos no próximo post.

Normalização

Dependendo do seu caso de uso, você pode querer normalizar cada dimensão na mesma escala, para que a distância ao longo de qualquer dimensão não influencie indevidamente a distância geral entre as observações. A mesma coisa foi discutida no algoritmo k-Means. Existem dois tipos de normalização possíveis:

A normalização de intervalo (redimensionamento) normaliza os dados para um intervalo de 0-1, subtraindo o valor mínimo de cada dimensão e, em seguida, dividindo pelo intervalo de valores nessa dimensão.

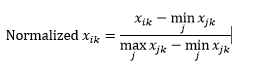
O primeiro problema com a normalização de intervalo é que um valor não visto pode ser normalizado além do intervalo 0-1. No entanto, isso geralmente não é uma preocupação para a maioria das métricas de distância, mas se o algoritmo não puder lidar com valores negativos, isso pode ser um problema. O segundo problema é que isso é altamente dependente de outliers. Se uma observação tiver um valor muito extremo (alto ou baixo) para uma dimensão, o valor normalizado para essa dimensão para outras observações será agrupado e perderá seus poderes discriminativos.

A normalização padrão (escala z) normaliza a dimensão para ter 0 média e 1 desvio padrão, subtraindo a média dessa dimensão de cada observação e, em seguida, dividindo pelo desvio padrão do valor dessa dimensão em todas as observações.

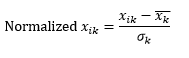
Isso geralmente mantém os dados na faixa de -5 a +5, aproximadamente, e evita a influência de valores extremos.

Simulamos o z-scaling de duas observações. Simulado, porque realmente precisamos de muito mais do que duas observações para calcular a média e o desvio padrão de cada dimensão, e assumimos esses dois números para cada dimensão aqui.

Então calcule a distância...

A distância euclidiana – também conhecida como distância “como o corvo voa” – é a distância mais curta no hiperespaço multidimensional entre dois pontos. Você está familiarizado com isso no plano 2D ou no espaço 3D (isto é uma linha), mas um conceito semelhante se estende a dimensões mais altas. A distância euclidiana entre vetores no espaço n-dimensional é calculada como

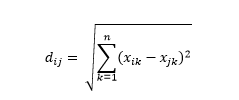
Para exemplos de vetores de dados transformados, isso é

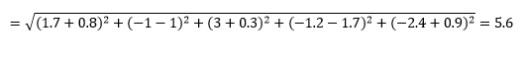
Essa é a métrica mais comum e geralmente muito adequada para a maioria das aplicações. Uma variante disso é a distância euclidiana ao quadrado, que é apenas a soma das diferenças ao quadrado.

A distância de Manhattan – nomeada por causa da grade Leste-Oeste-Norte-Sul como a estrutura das ruas de Manhattan em Nova York – é a distância entre dois pontos ao atravessar paralelamente aos eixos.

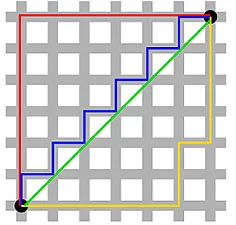
Distância de Manhattan
Distância euclidiana

Isso é calculado como

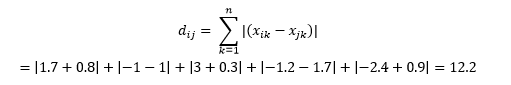
Isso pode ser útil em alguns aplicativos em que a distância é usada no sentido físico real, em vez do sentido de “dissimilaridade” do aprendizado de máquina. Por exemplo, se você precisar calcular a distância percorrida pelo caminhão de bombeiros para chegar a um ponto, usar isso é mais prático.

A distância de Camberra é uma variante ponderada da distância de Manhattan e é calculada como

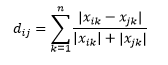
A distância L-norm é a extensão acima de dois – ou você pode dizer que acima de dois são casos específicos de distância L-norm – e é definida como

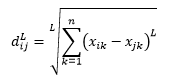
onde L é um inteiro positivo. Não encontrei nenhum caso em que precisei usar isso, mas ainda é bom saber a possibilidade. Por exemplo, a distância de 3 normas será

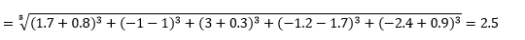
Observe que L geralmente deve ser um número inteiro par, pois não queremos que as contribuições de distância positivas ou negativas sejam canceladas.

A distância de Minkowski é uma generalização da distância da norma L, onde L pode assumir qualquer valor de 0 até incluir valores fracionários. A distância de Minkowski de ordem p é definida como

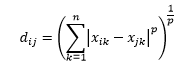
A distância do cosseno é a medida do ângulo entre dois vetores, cada um representando duas observações, e formado pela junção do ponto de dados à origem. A distância do cosseno varia de 0 (exatamente o mesmo) a 1 (sem conexão) e é calculada como

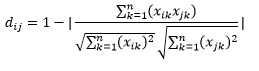
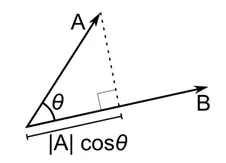
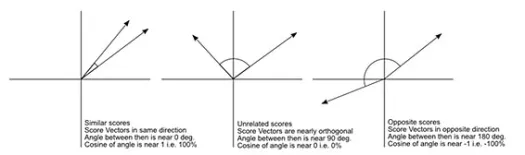
Embora esta seja uma medida de distância mais comum ao trabalhar com dados categóricos, isso também pode ser definido para vetor numérico. Para nossos vetores numéricos, isso será

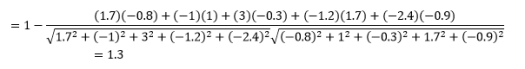
Mas cuidado com as ressalvas…

Você sabia que isso ia acontecer, não é? Se a análise fosse apenas um monte de fórmulas matemáticas, não precisaríamos de pessoas inteligentes como você para fazer isso.

A primeira coisa a notar é que as distâncias calculadas por diferentes métricas são diferentes. Você pode ser tentado a pensar que a distância do cosseno de 1,3 é a menor e, portanto, indica que os vetores estão mais próximos, mas essa não é a maneira correta de interpretar. Distâncias entre diferentes métodos não podem ser comparadas, e apenas distâncias entre diferentes pares de observações sob o mesmo método podem ser comparadas. As distâncias têm um significado relativo e nenhum significado absoluto por si mesmas .

Isso leva à próxima pergunta de como selecionar a métrica de distância correta. Infelizmente, não há uma resposta verdadeira. Dependendo do tipo de dados, contexto, problema de negócios, aplicativo e método de treinamento do modelo, métricas diferentes fornecem resultados diferentes. Você terá que usar o julgamento, fazer suposições ou testar o desempenho do modelo para decidir sobre a métrica correta .

A segunda advertência é a minha frequentemente repetida sobre a maldição da dimensionalidade. Em dimensões mais altas, as distâncias não se comportam da maneira que intuitivamente pensamos , e o analista deve ser extremamente cauteloso ao usar qualquer métrica.

A terceira ressalva é sobre a relação entre as distâncias entre três observações. Algumas métricas suportam a desigualdade triangular e outras não . A desigualdade triangular implica que é sempre mais curto ir do ponto i ao ponto j diretamente, em vez de passar por qualquer ponto intermediário k. Matematicamente,

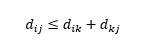
Dependendo da sua aplicação, isso pode ou não ser uma propriedade obrigatória da métrica de distância.

Ah, mais uma coisa, “distância” é o oposto de “semelhança”. Quanto maior a distância, menor a semelhança e vice-versa. Os algoritmos de agrupamento funcionam em distâncias e os algoritmos de recomendação funcionam em similaridade, mas essencialmente eles estão falando sobre a mesma coisa.

Então, como você pode transformar o número de distância em número de similaridade?