Blestemul dimensionalității
Publicat: 2015-07-08Ce este Blestemul Dimensionalității
Blestemul dimensionalității se referă la proprietățile non-intuitive ale datelor observate atunci când se lucrează în spațiu de dimensiuni înalte*, în special legate de utilizare și interpretarea distanțelor și volumelor. Acesta este unul dintre subiectele mele preferate din Învățare automată și statistică, deoarece are aplicații largi (nu specifice oricărei metode de învățare automată), este foarte contraintuitiv și, prin urmare, uimitor, are aplicații profunde pentru oricare dintre tehnicile de analiză și are un nume „mișto” înfricoșător ca un blestem egiptean!
Pentru o înțelegere rapidă, luați în considerare acest exemplu: Să spuneți că ați scăpat o monedă pe o linie de 100 de metri. Cum îl găsești? Simplu, mergeți pe linie și căutați. Dar dacă este de 100 x 100 mp. camp? Deja devine greu să încerci să cauți un teren de fotbal (aproximativ) pentru o singură monedă. Dar dacă este 100 x 100 x 100 cu.m spațiu?! Știi, terenul de fotbal are acum treizeci de etaje. Noroc să găsești o monedă acolo! Acesta, în esență, este „blestemul dimensionalității”.
Multe metode ML folosesc Măsurarea distanței
Majoritatea metodelor de segmentare și grupare se bazează pe calcularea distanțelor dintre observații. Segmentarea k-Means binecunoscută atribuie puncte celui mai apropiat centru. DBSCAN și clusteringul ierarhic au necesitat, de asemenea, metrici de distanță. Algoritmii de detectare a valorii aberante bazate pe distribuție și densitate folosesc, de asemenea, distanța față de alte distanțe pentru a marca valorile aberante.
Soluțiile de clasificare supravegheată, cum ar fi metoda k-Nearest Neighbors , folosesc și distanța dintre observații pentru a atribui o clasă unei observații necunoscute. Metoda Support Vector Machine implică transformarea observațiilor în jurul unor nuclee selectate pe baza distanței dintre observație și nucleu.
Forma comună a sistemelor de recomandare implică similitudinea bazată pe distanță între vectorii de atribute ale utilizatorului și ale articolului. Chiar și atunci când sunt utilizate alte forme de distanțe, numărul de dimensiuni joacă un rol în proiectarea analitică.
Una dintre cele mai comune metrici ale distanței este metrica distanței euclidiane, care este pur și simplu distanța liniară dintre două puncte din hiperspațiul multidimensional. Distanța euclidiană pentru punctul i și punctul j din spațiul n dimensional poate fi calculată ca:
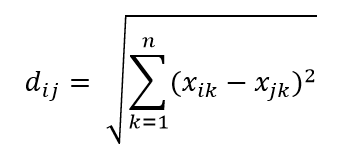
Distanța face ravagii în dimensiunile înalte
Luați în considerare un proces simplu de eșantionare a datelor. Să presupunem că caseta exterioară neagră din Fig. 1 este un univers de date cu distribuție uniformă a punctelor de date pe întreg volumul și că vrem să eșantionăm 1% din observații, așa cum sunt încadrate de caseta roșie din interior. Cutia neagră este un hiper-cub în spațiul multidimensional, fiecare parte reprezentând intervalul de valori în acea dimensiune. Pentru un exemplu simplu tridimensional din Fig. 1, putem avea următorul interval:
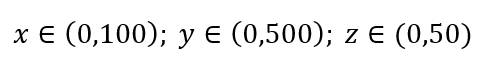
Figura 1: Eșantionare
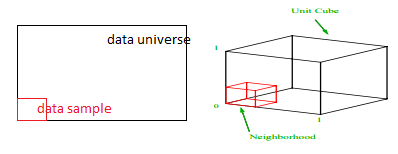
Care este proporția din fiecare interval ar trebui să eșantionăm pentru a obține acel eșantion de 1%? Pentru 2 dimensiuni, 10% din interval va obține o eșantionare totală de 1%, așa că putem selecta x∈(0,10) și y∈(0,50) și ne așteptăm să captăm 1% din toate observațiile. Acest lucru se datorează faptului că 10%2=1%. Vă așteptați ca această proporție să fie mai mare sau mai mică pentru 3 dimensiuni?
Chiar dacă căutarea noastră este acum într-o direcție suplimentară, proporțional crește de fapt la 21,5%. Și nu doar crește, ci doar pentru o dimensiune suplimentară, se dublează! Și puteți vedea că trebuie să acoperim aproape o cincime din fiecare dimensiune doar pentru a obține o sutime din total! În 10 dimensiuni, această proporție este de 63%, iar în 100 de dimensiuni – ceea ce nu este un număr neobișnuit de dimensiuni în orice învățare automată din viața reală – trebuie să eșantioneze 95% din interval de-a lungul fiecărei dimensiuni pentru a eșantiona 1% din observații! Acest rezultat uluitor se întâmplă deoarece, în dimensiuni mari, răspândirea punctelor de date devine mai mare, chiar dacă acestea sunt răspândite uniform.

Acest lucru are consecințe în ceea ce privește proiectarea experimentului și eșantionarea. Procesul devine foarte costisitor din punct de vedere computațional, chiar și în măsura în care eșantionarea se apropie asimptotic de populație, în ciuda dimensiunii eșantionului care rămâne mult mai mică decât populația.
Luați în considerare o altă consecință uriașă a dimensionalității ridicate. Mulți algoritmi măsoară distanța dintre două puncte de date pentru a defini un fel de apropiere (DBSCAN, Kernels, k-Nearest Neighbour) în raport cu un prag de distanță predefinit. În 2 dimensiuni, ne putem imagina că două puncte sunt aproape dacă unul se află pe o anumită rază a altuia. Luați în considerare imaginea din stânga din Fig. 2. Care este cota punctelor uniform distanțate în pătratul negru care se încadrează în interiorul cercului roșu? Cam asta este
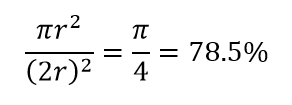
Figura 2: Apropiere
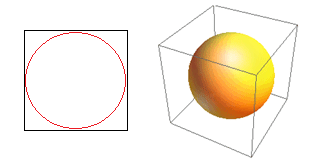
Deci, dacă încadrezi cel mai mare cerc posibil în interiorul pătratului, acoperiți 78% din pătrat. Cu toate acestea, cea mai mare sferă posibilă în interiorul cubului acoperă doar
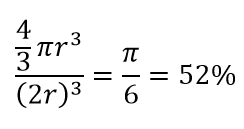
a volumului. Acest volum se reduce exponențial la 0,24% pentru doar 10 dimensiuni! Ceea ce înseamnă în esență că, în lumea cu dimensiuni înalte, fiecare punct de date este la colțuri și nimic nu este cu adevărat centru de volum, sau cu alte cuvinte, volumul central se reduce la nimic pentru că nu există (aproape) niciun centru! Acest lucru are consecințe uriașe ale algoritmilor de grupare bazați pe distanță. Toate distanțele încep să arate la fel și orice distanță mai mare sau mai mică decât cealaltă este o fluctuație mai aleatorie a datelor, mai degrabă decât orice măsură de diferență!
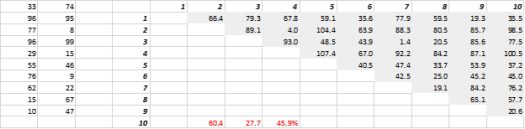
Fig. 3 prezintă date 2-D generate aleatoriu și distanțele corespunzătoare all-to-all. Coeficientul de variație a distanței, calculat ca abaterea standard împărțită la medie, este de 45,9%. Numărul corespunzător de date 5-D generate în mod similar este de 26,5%, iar pentru 10-D este de 19,1%. Desigur, acesta este un eșantion, dar tendința susține concluzia că, în dimensiuni mari, fiecare distanță este aproximativ aceeași și nici una nu este aproape sau departe!
Figura 3: Clustering la distanță
Dimensiunea înaltă afectează și alte lucruri
Pe lângă distanțe și volume, numărul de dimensiuni creează alte probleme practice. Cerințele de rulare a soluției și de memorie de sistem cresc adesea neliniar odată cu creșterea numărului de dimensiuni. Datorită creșterii exponențiale a soluțiilor fezabile, multe metode de optimizare nu pot atinge optime globale și trebuie să se mulțumească cu optime locale. În plus, în loc de soluție în formă închisă, optimizarea trebuie să utilizeze algoritmi bazați pe căutare, cum ar fi coborârea gradientului, algoritmul genetic și recoacere simulată. Mai multe dimensiuni introduc posibilitatea de corelare și estimarea parametrilor poate deveni dificilă în abordările de regresie.
De-a face cu dimensiunea înaltă
Aceasta va fi o postare separată pe blog în sine, dar analiza corelației, gruparea, valoarea informațiilor, factorul de inflație a varianței, analiza componentelor principale sunt câteva dintre modalitățile prin care numărul de dimensiuni poate fi redus.
* Numărul de variabile, observații sau caracteristici din care este format un punct de date se numește dimensiunea datelor. De exemplu, orice punct din spațiu poate fi reprezentat folosind 3 coordonate de lungime, lățime și înălțime și are 3 dimensiuni
