Estimarea densității folosind histograme

Funcțiile de densitate de probabilitate (PDF) descriu probabilitatea de a observa o variabilă aleatoare continuă într-o anumită regiune a spațiului. Pentru variabila aleatoare unidimensională X, amintiți-vă că PDF f(x) urmează proprietățile care

Probabilitatea ca variabila să ia valori între

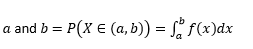
Probabilitatea ca variabila să ia valori exact egale cu

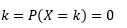
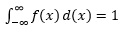
Estimarea unui astfel de PDF din eșantion de observații este o problemă comună în Machine Learning. Acest lucru este util în mulți algoritmi de detectare a valorii aberante, în care căutăm să estimăm distribuția „adevărată” pe baza observațiilor eșantionului și apoi să clasificăm unele dintre observațiile existente sau noi ca fiind excepționale sau nu. De exemplu, un asigurător auto interesat să detecteze frauda ar putea examina cererea de sumă de despăgubire pentru fiecare tip de caroserie, de exemplu, înlocuirea barei de protecție și poate marca pentru fraudă potențială orice sumă care este prea mare. Printr-un alt exemplu, un psiholog pentru copii poate examina timpul necesar pentru a îndeplini o anumită sarcină pentru diferiți copii și poate marca acei copii cărora le ia prea mult sau prea scurt timp pentru investigații potențiale.

În această postare pe blog, discutăm cum putem învăța PDF-ul din eșantion de observații , astfel încât să putem calcula probabilitatea pentru fiecare observație și să decidem dacă este o apariție obișnuită sau rară.

Estimarea densității folosind histograma

Mai întâi generăm câteva date aleatorii pentru demonstrație.

set.seed(123)
data <- c(rnorm(200, 10, 20), rnorm(200, 60, 30), runif(200, 120, 180)) # 600 points

Apoi, le vizualizăm pentru înțelegerea noastră, folosind histograma, ca în Figura 1.

# Plot 1
hist(data, breaks=50, freq=F, main="Univariate Distribution", xlab="Data Value")
# Plot 2
hist(data, breaks=20, freq=F, main="", xlab="20 Data Bins", col='red', border='red')
par(new=T)
hist(data, breaks=100, freq=F, main="Univariate Distribution", xlab=NULL, xaxt='n', yaxt='n')

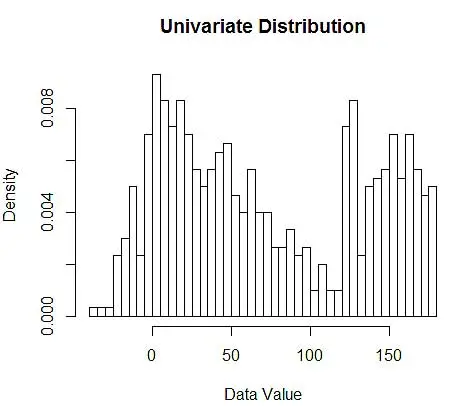
În timp ce histogramele sunt diagrame pentru vizualizarea datelor, puteți vedea, de asemenea, că sunt prima noastră estimare a densității. Mai precis, putem estima densitatea împărțind datele în compartimente și presupunând că densitatea este constantă în intervalul respectiv și are o valoare egală cu numărul de observații care se încadrează în acel bin ca proporție din numărul total de observații

Prin urmare, PDF estimat este

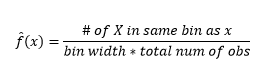
Și vă dați seama că ați făcut presupuneri despre lățimea binului, care va afecta estimarea densității. Prin urmare , bin-width este un parametru pentru modelul de estimare a densității folosind histograma . Cu toate acestea, faptul trecut cu vederea este că lucrăm și cu încă un parametru – care este poziția de pornire a primului bin . Puteți vedea cum poate afecta acest lucru estimările de densitate pentru toate recipientele. Pentru a vedea impactul lățimii bin, Figura 2 suprapune estimările de densitate cu histograme de 20 și 100 de bin. Uitați-vă la regiunea înconjurată, unde mai puține/mai grosiere recipiente oferă o estimare plată a densității, în timp ce multe/mai fine recipiente oferă o estimare a densității variate. Pentru punctul galben, estimările de densitate vor varia de la 0,004 la 0,008 de la două modele diferite.

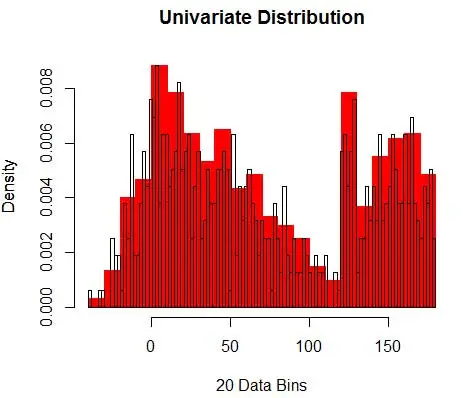
Astfel, selectarea corectă a parametrilor este crucială pentru a obține corect estimarea densității. Vom ajunge la asta, dar rețineți că există și alte probleme cu histogramele. Estimările de densitate folosind histograme sunt destul de sacadate și discontinue . Densitatea este plată pentru un coș și apoi se schimbă brusc drastic pentru un punct infinitezimal în afara coșului. Acest lucru face consecințele unei estimări greșite și mai grave pentru problemele practice.

În cele din urmă, am lucrat cu variabile unidimensionale pentru a facilita ilustrarea, dar în practică majoritatea problemelor sunt multi-dimensionale. Deoarece numărul de containere crește exponențial cu numărul de dimensiuni, crește și numărul de observații necesare pentru estimarea densității . De fapt, este plauzibil că, deși au milioane de observații, multe coșuri rămân goale sau conțin observații cu o singură cifră. Cu doar 50 de containere fiecare în doar 3 dimensiuni, avem 503=125000 de celule care trebuie populate. Aceasta înseamnă o medie de 8 observații pe celulă, presupunând o distribuție uniformă, un milion de date de antrenament de observație.

Cum se selectează parametrii potriviți?

Pentru bin-width n număr de observații N pentru bin J proporția de observații este

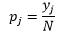
iar densitatea estimată este

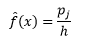
Teoria statistică demonstrează că, în timp ce f(x) este valoarea așteptată a densității în bin, varianța densității este

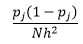
Deși putem obține o estimare mai bună a densității prin reducerea lățimii bin-ului n, creștem varianța estimării, deoarece putem simți intuitiv că lățimea bin-ului este prea mică. Putem folosi tehnica de validare încrucișată pentru a estima setul optim de parametri. Putem estima densitatea folosind toate observațiile, cu excepția uneia, și apoi să calculăm densitatea acelei observații omise și să măsurăm eroarea în estimare. Rezolvarea matematică a acestui lucru pentru histograme oferă o soluție în formă închisă pentru funcția de pierdere pentru lățimea bin-ului dată.

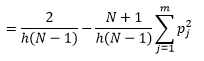
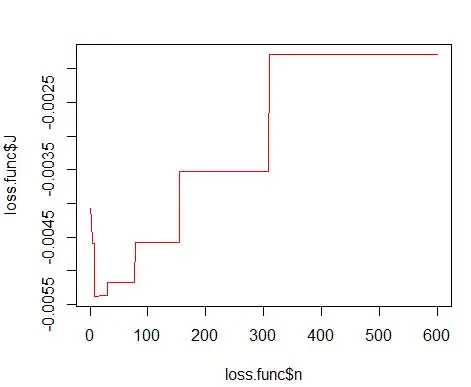
unde m este numărul de containere. Detaliile tehnice de mai sus sunt în această prelegere [pdf] . Putem reprezenta grafic această funcție de pierdere pentru diferite numere de containere (Figura 3)

getLoss <- function(n.break) {
N <- 600
res <- hist(data, breaks=n.break, freq=F)
bin <- as.numeric(res$breaks)
h <- bin[2]-bin[1]
p <- res$density
p <- p * h
return ( 2/(h*(N-1)) - ( (N+1)/(h*(N-1))*sum(p*p) ) )
}
loss.func <- data.frame(n=1:600)
loss.func$J <- sapply(loss.func$n, function(x) getLoss(x))
# Plot 3
plot(loss.func$n, loss.func$J, col='red', type='l')
opt.break <- max(loss.func[loss.func$J == min(loss.func$J), 'n'])
print(opt.break)
# Plot 4
hist(data, breaks=opt.break, freq=F, main="Univariate Distribution", xlab="15 Data Bins")

și obțineți numărul optim ca 15. De fapt, orice de la 8 la 15 este bine.

În consecință, sub Figura 4 este estimarea densității care echilibrează valorile densității și granularitatea (cu un compromis optim de variație de părtinire).

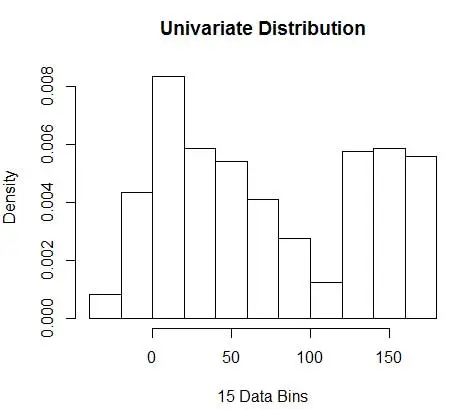
Dacă te simți puțin neliniștit în acest moment, atunci sunt cu tine. Chiar dacă numărul de coșuri este optim din punct de vedere matematic, pare o estimare prea grosieră. Nu există niciun sentiment intuitiv de ce am făcut cea mai bună treabă. Și să nu uităm de alte preocupări legate de poziția de pornire, estimarea discontinuă și blestemul dimensionalității. Nu disperați, există o cale mai bună. În postarea următoare vom vorbi despre Estimarea densității folosind Kernels.