Măsurarea distanței în hiperspațiu

Oricine familiarizat superficial cu tehnicile analitice ar fi observat o mulțime de algoritmi care se bazează pe distanțe dintre punctele de date pentru aplicarea lor. Fiecare observație, sau instanță de date, este de obicei reprezentată ca un vector multidimensional, iar intrarea în algoritm necesită distanțe între fiecare pereche de astfel de observații.

Metoda de calcul a distanței depinde de tipul de date - numerice, categoriale sau mixte. Unii algoritmi se aplică doar unei clase de observații, în timp ce alții funcționează pe mai multe. În această postare, vom discuta despre măsurile de distanță care funcționează pe date numerice. Există probabil mai multe moduri în care distanța poate fi măsurată în hiperspațiul multidimensional decât cele care pot fi acoperite într-o singură postare pe blog și oricând se pot inventa modalități mai noi, dar ne uităm la unele dintre metricile comune ale distanței și meritele lor relative.

În scopul restului postării pe blog, sugerăm

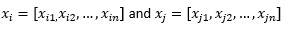
pentru a se referi la doi observații sau vectori de date.

Mai întâi pregătiți datele...

Înainte de a revizui diferite valori de distanță, trebuie să pregătim datele:

Transformare în vector numeric

Pentru observația mixtă, care conține atât dimensiuni numerice, cât și dimensiuni categoriale, primul pas este transformarea efectivă a dimensiunii categoriale în dimensiune(e) numerică. O dimensiune categorială cu trei valori potențiale poate fi transformată în două sau trei dimensiuni numerice cu valori binare. Deoarece această variabilă categorică ia în mod necesar una din trei valori, una dintre cele trei dimensiuni numerice va fi perfect corelată cu celelalte două. Acest lucru poate fi sau nu în regulă, în funcție de aplicația dvs.

Dacă observația este pur categorică, cum ar fi șirul de text (propoziții cu lungime variabilă) sau secvența genomului (secvențe cu lungime fixă), atunci o metrică specială a distanței poate fi aplicată direct fără transformarea datelor în format numeric. Vom discuta despre acești algoritmi în postarea următoare.

Normalizare

În funcție de cazul dvs. de utilizare, este posibil să doriți să normalizați fiecare dimensiune la aceeași scară, astfel încât distanța de-a lungul oricărei dimensiuni să nu influențeze în mod nejustificat distanța totală dintre observații. Același lucru a fost discutat în algoritmul k-Means. Există două tipuri de normalizare posibile:

Normalizarea intervalului (rescalare) normalizează datele pentru a fi în intervalul 0-1, scăzând valoarea minimă din fiecare dimensiune și apoi împărțind la intervalul de valori din acea dimensiune.

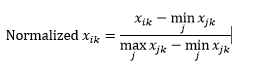
Prima problemă cu normalizarea intervalului este că o valoare nevăzută poate fi normalizată dincolo de intervalul 0-1. Cu toate acestea, acest lucru nu este, în general, o preocupare pentru majoritatea măsurătorilor de distanță, dar dacă algoritmul nu poate gestiona valorile negative, atunci aceasta poate fi o problemă. A doua problemă este că aceasta depinde foarte mult de valori aberante. Dacă o observație are o valoare foarte extremă (înaltă sau scăzută) pentru o dimensiune, valoarea normalizată pentru acea dimensiune pentru alte observații va fi înghesuită și își va pierde puterile discriminatorii.

Normalizarea standard (scalarea z) normalizează dimensiunea pentru a avea 0 medie și 1 abatere standard, prin scăderea mediei din acea dimensiune a fiecărei observații și apoi împărțirea la abaterea standard a valorii acelei dimensiuni în toate observațiile.

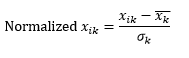
Acest lucru păstrează, în general, datele în intervalul -5 până la +5, aproximativ și evită influența unei valori extreme.

Am simulat scalarea z a două observații. Simulat, deoarece avem nevoie de mai mult de două observații pentru a calcula media și abaterea standard a fiecărei dimensiuni și am presupus ambele numere pentru fiecare dimensiune aici.

Apoi calculează distanța...

Distanța euclidiană – și anume distanța „în volan” – este cea mai scurtă distanță din hiperspațiul multidimensional între două puncte. Sunteți familiarizat cu acest lucru în plan 2D sau spațiu 3D (aceasta este o linie), dar un concept similar se extinde la dimensiuni mai mari. Distanța euclidiană dintre vectori din spațiul n-dimensional este calculată ca

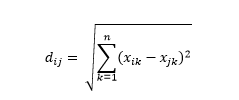
Pentru exemplele de vector de date transformate, aceasta este

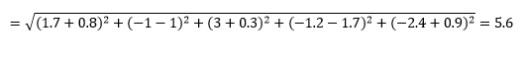
Aceasta este cea mai comună metrică și adesea foarte potrivită pentru majoritatea aplicațiilor. O variantă a acesteia este distanța pătrat-euclidiană, care este doar suma diferențelor pătrate.

Distanța Manhattan – numită datorită structurii de tip grilă Est-Vest-Nord-Sud a străzilor din Manhattan din New York – este distanța dintre două puncte atunci când se traversează paralel cu axele.

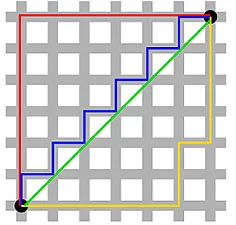
Distanța Manhattan
Distanta euclidiana

Aceasta este calculată ca

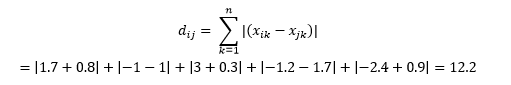
Acest lucru poate fi util în anumite aplicații în care distanța este folosită în sens real, fizic, mai degrabă decât în ​​sensul de „asemănare” de învățare automată. De exemplu, dacă trebuie să calculați distanța parcursă de camionul de pompieri pentru a ajunge la un punct, atunci folosirea acestuia este mai practică.

Distanța Canberra este o variantă ponderată a distanței Manhattan și este calculată ca

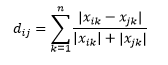
Distanța L-norma este extinderea de peste doi – sau puteți spune că mai sus de două sunt cazuri specifice de distanță L-norma – și este definită ca

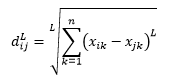
unde L este un întreg pozitiv. Nu am întâlnit niciun caz în care să fi trebuit să folosesc acest lucru, dar este încă o posibilitate bună de știut. De exemplu, distanța de 3 norme va fi

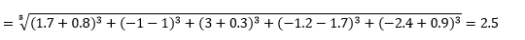
Rețineți că L ar trebui să fie, în general, chiar întreg, deoarece nu dorim să se anuleze contribuțiile la distanță pozitive sau negative.

Distanța Minkowski este generalizarea distanței L-normă, unde L ar putea lua orice valoare de la 0 până la includerea valorilor fracționale. Distanța Minkowski de ordinul p este definită ca

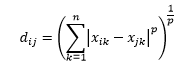
Distanța cosinus este măsura unghiului dintre doi vectori, fiecare reprezentând două observații, și formată prin unirea punctului de date la origine. Distanța cosinusului variază de la 0 (exact aceeași) la 1 (fără conexiune) și este calculată ca

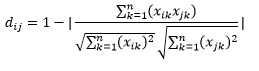
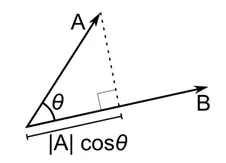
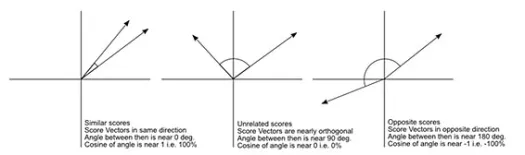
Deși aceasta este o măsură mai comună a distanței atunci când se lucrează cu date categorice, aceasta poate fi definită și pentru vectorul numeric. Pentru vectorii noștri numerici, aceasta va fi

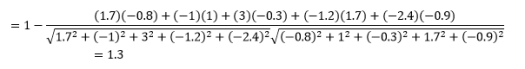
Dar ține cont de avertismente...

Știai că asta va veni, nu-i așa? Dacă analitica ar fi fost doar o grămadă de formule matematice, nu vom avea nevoie de oameni deștepți ca tine să o facă.

Primul lucru de remarcat este că distanțele calculate de diferite valori sunt diferite. Ați putea fi tentat să credeți că distanța Cosinus de 1,3 este cea mai mică și, prin urmare, indică că vectorii sunt cei mai apropiați, dar aceasta nu este modalitatea corectă de interpretare. Distanțele dintre diferite metode nu pot fi comparate și doar distanțele dintre diferite perechi de observații în cadrul aceleiași metode pot fi comparate. Distanțele au semnificație relativă și nici un sens absolut în sine .

Acest lucru duce la următoarea întrebare despre cum să selectați metrica distanței corecte. Din păcate, nu există un răspuns adevărat. În funcție de tipul de date, context, problema de afaceri, aplicație și metoda de formare a modelului, diferite metrice dau rezultate diferite. Va trebui să folosiți raționamentul, să faceți ipoteze sau să testați performanța modelului pentru a decide valoarea corectă .

Al doilea avertisment este unul pe care l-am repetat adesea despre blestemul dimensionalității. În dimensiuni mai mari, distanțele nu se comportă așa cum credem intuitiv că se comportă , iar analistul trebuie să fie extrem de precaut când folosește orice valoare.

Al treilea avertisment se referă la relația dintre distanțe între trei observații. Unele valori acceptă inegalitatea triunghiulară, iar altele nu . Inegalitatea triunghiulară implică faptul că este întotdeauna cel mai scurt să mergi direct de la punctul i la punctul j, mai degrabă decât prin orice punct intermediar k. Din punct de vedere matematic,

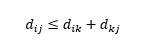
În funcție de aplicația dvs., aceasta poate fi sau nu proprietatea necesară a metricii distanței.

O, încă ceva, „distanța” este opusul „asemănării”. Mai mare distanța, mai mică asemănarea și invers. Algoritmii de grupare funcționează pe distanțe, iar algoritmii de recomandare funcționează pe similaritate, dar în esență vorbesc despre același lucru.

Deci, cum poți transforma numărul de distanță în număr de asemănare?