Проклятие размерности
Опубликовано: 2015-07-08Что такое проклятие размерности
Проклятие размерности относится к неинтуитивным свойствам данных, наблюдаемым при работе в многомерном пространстве*, особенно связанным с удобством использования и интерпретацией расстояний и объемов. Это одна из моих любимых тем в машинном обучении и статистике, поскольку она имеет широкое применение (не относящееся к какому-либо методу машинного обучения), она очень нелогична и, следовательно, внушает благоговейный трепет, имеет глубокое применение для любого из методов аналитики и у него "крутое" страшное имя, как какое-то египетское проклятие!
Для быстрого понимания рассмотрим следующий пример: скажем, вы бросили монету на 100-метровой линии. Как вы его находите? Просто, просто идите по линии и ищите. А если это 100 х 100 кв.м. поле? Уже становится тяжело пытаться обыскать (примерно) футбольное поле в поисках одной монеты. А если это пространство 100 х 100 х 100 кубометров?! Вы знаете, футбольное поле теперь имеет высоту тридцатиэтажного дома. Удачи найти там монету! Что, по сути, и есть «проклятие размерности».
Многие методы ML используют измерение расстояния
Большинство методов сегментации и кластеризации основаны на вычислении расстояний между наблюдениями. Хорошо известная сегментация k-средних присваивает точки ближайшему центру. DBSCAN и иерархическая кластеризация также требовали показателей расстояния. Алгоритмы обнаружения выбросов на основе распределения и плотности также используют расстояние относительно других расстояний, чтобы отметить выбросы.
Решения контролируемой классификации, такие как метод k-ближайших соседей , также используют расстояние между наблюдениями для присвоения класса неизвестному наблюдению. Метод машины опорных векторов включает в себя преобразование наблюдений вокруг выбранных ядер на основе расстояния между наблюдением и ядром.
Обычная форма рекомендательных систем включает сходство на основе расстояния между векторами атрибутов пользователя и элемента. Даже когда используются другие формы расстояний, количество измерений играет роль в аналитическом дизайне.
Одной из наиболее распространенных метрик расстояния является метрика евклидова расстояния, которая представляет собой просто линейное расстояние между двумя точками в многомерном гиперпространстве. Евклидово расстояние для точки i и точки j в n-мерном пространстве можно вычислить как:
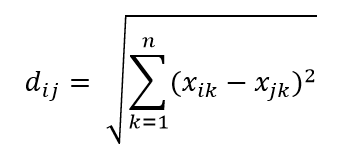
Расстояние играет разрушительную роль в большом измерении
Рассмотрим простой процесс выборки данных. Предположим, что черный внешний прямоугольник на рис. 1 представляет собой совокупность данных с равномерным распределением точек данных по всему объему, и что мы хотим выбрать 1% наблюдений, заключенных внутри красного прямоугольника. Черный ящик представляет собой гиперкуб в многомерном пространстве, каждая сторона которого представляет диапазон значений в этом измерении. Для простого трехмерного примера на рис. 1 у нас может быть следующий диапазон:
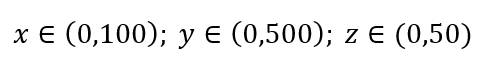
Рисунок 1: Выборка
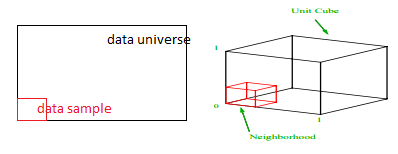
Какова доля каждого диапазона, которую мы должны взять, чтобы получить этот 1% выборки? Для 2-мерного измерения 10 % диапазона обеспечивают общую выборку в 1 %, поэтому мы можем выбрать x∈(0,10) и y∈(0,50) и ожидать захвата 1% всех наблюдений. Это потому, что 10%2=1%. Ожидаете ли вы, что эта пропорция будет выше или ниже для трехмерного изображения?
Несмотря на то, что наш поиск теперь идет в другом направлении, пропорциональное значение на самом деле увеличивается до 21,5%. И не просто увеличивается, всего за одно дополнительное измерение, а удваивается! И вы можете видеть, что нам нужно охватить почти одну пятую каждого измерения, чтобы получить одну сотую от общего! В 10-мерном пространстве эта пропорция составляет 63%, а в 100-мерном — что не является редкостью в любом реальном машинном обучении — нужно отобрать 95% диапазона по каждому измерению, чтобы отобрать 1% наблюдений! Этот умопомрачительный результат возникает из-за того, что в больших измерениях разброс точек данных становится больше, даже если они распределены равномерно.

Это имеет последствия с точки зрения дизайна эксперимента и отбора проб. Процесс становится очень затратным с вычислительной точки зрения, даже в той степени, в которой выборка асимптотически приближается к совокупности, несмотря на то, что размер выборки остается намного меньше, чем совокупность.
Рассмотрим еще одно огромное следствие высокой размерности. Многие алгоритмы измеряют расстояние между двумя точками данных, чтобы определить своего рода близость (DBSCAN, Kernels, k-Nearest Neighbour) относительно некоторого предварительно определенного порога расстояния. В двух измерениях мы можем представить себе, что две точки находятся рядом, если одна из них находится в пределах определенного радиуса от другой. Рассмотрим левое изображение на рис. 2. Какая доля равномерно расположенных точек внутри черного квадрата попадает внутрь красного круга? Это о
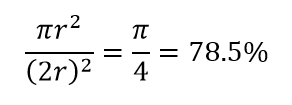
Рисунок 2: Близость
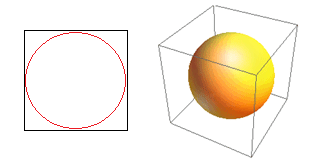
Таким образом, если вы поместите самый большой круг внутри квадрата, вы покроете 78% площади. Тем не менее, самая большая сфера, возможная внутри куба, покрывает только
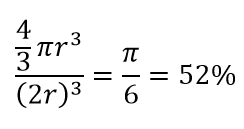
объема. Этот объем уменьшается в геометрической прогрессии до 0,24% только для 10-мерного измерения! По сути, это означает, что в многомерном мире каждая точка данных находится по углам, и ничто на самом деле не является центром объема, или, другими словами, центральный объем сводится к нулю, потому что центра (почти) нет! Это имеет огромные последствия для алгоритмов кластеризации на основе расстояния. Все расстояния начинают выглядеть одинаковыми, и любое расстояние больше или меньше другого является скорее случайным колебанием данных, чем какой-либо мерой несходства!
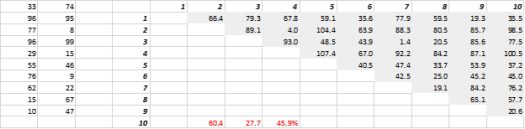
На рис. 3 показаны случайно сгенерированные двумерные данные и соответствующие расстояния между всеми. Коэффициент вариации расстояния, рассчитанный как стандартное отклонение, деленное на среднее значение, составляет 45,9%. Соответствующее количество аналогично сгенерированных 5-D данных составляет 26,5%, а для 10-D — 19,1%. По общему признанию, это одна выборка, но тенденция подтверждает вывод о том, что в больших измерениях все расстояния примерно одинаковы, и нет ни близкого, ни далекого!
Рисунок 3: Кластеризация по расстоянию
Высокая размерность влияет и на другие вещи
Помимо расстояний и объемов, число измерений создает и другие практические проблемы. Требования к времени выполнения решения и системной памяти часто нелинейно возрастают с увеличением количества измерений. Из-за экспоненциального роста допустимых решений многие методы оптимизации не могут достичь глобальных оптимумов и вынуждены обходиться локальными оптимумами. Кроме того, вместо решения в закрытой форме оптимизация должна использовать алгоритмы на основе поиска, такие как градиентный спуск, генетический алгоритм и имитация отжига. Дополнительные измерения открывают возможность корреляции, и оценка параметров может стать сложной в регрессионных подходах.
Работа с большими размерами
Это будет отдельный пост в блоге сам по себе, но корреляционный анализ, кластеризация, информационная ценность, коэффициент инфляции дисперсии, анализ основных компонентов — вот некоторые из способов, которыми можно уменьшить количество измерений.
* Количество переменных, наблюдений или признаков, из которых состоит точка данных, называется размерностью данных. Например, любая точка в пространстве может быть представлена с использованием 3 координат длины, ширины и высоты и имеет 3 измерения.
