Измерение расстояния в гиперпространстве
Опубликовано: 2016-01-10Любой, кто поверхностно знаком с аналитическими методами, заметил бы множество алгоритмов, использующих в своих приложениях расстояния между точками данных. Каждое наблюдение или экземпляр данных обычно представляется в виде многомерного вектора, и для ввода в алгоритм требуются расстояния между каждой парой таких наблюдений.
Метод расчета расстояния зависит от типа данных – числовых, категорийных или смешанных. Некоторые из алгоритмов применяются только к одному классу наблюдений, в то время как другие работают с несколькими. В этом посте мы обсудим меры расстояния, которые работают с числовыми данными. Возможно, существует больше способов измерения расстояния в многомерном гиперпространстве, чем те, которые могут быть описаны в одном сообщении в блоге, и всегда можно изобрести новые способы, но мы рассмотрим некоторые распространенные метрики расстояния и их относительные достоинства.
Для остальной части сообщения в блоге мы подразумеваем
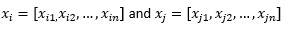
для обозначения двух наблюдений или векторов данных.
Сначала подготовьте данные…
Прежде чем мы рассмотрим различные показатели расстояния, нам нужно подготовить данные:
Преобразование в числовой вектор
Для смешанного наблюдения, которое содержит как числовые, так и категориальные измерения, первым шагом является фактическое преобразование категориального измерения в числовое измерение (я). Категориальное измерение с тремя потенциальными значениями можно превратить в два или три числовых измерения с двоичными значениями. Поскольку эта категориальная переменная обязательно принимает одно из трех значений, одно из трех числовых измерений будет идеально коррелировать с двумя другими. Это может быть или не быть в зависимости от вашего приложения.

Если наблюдение носит чисто категориальный характер, например, текстовая строка (предложения переменной длины) или последовательность генома (последовательности фиксированной длины), то некоторые специальные метрики расстояния могут быть применены напрямую без преобразования данных в числовой формат. Мы обсудим эти алгоритмы в следующем посте.
Нормализация
В зависимости от вашего варианта использования вы можете нормализовать каждое измерение в одном масштабе, чтобы расстояние по любому одному измерению не оказывало чрезмерного влияния на общее расстояние между наблюдениями. То же самое обсуждалось в алгоритме k-Means. Возможны два вида нормализации:
Нормализация диапазона (масштабирование) нормализует данные, чтобы они находились в диапазоне 0–1, путем вычитания минимального значения из каждого измерения и последующего деления на диапазон значений в этом измерении.
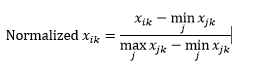
Первая проблема с нормализацией диапазона заключается в том, что невидимое значение может быть нормализовано за пределами диапазона 0-1. Хотя это, как правило, не касается большинства показателей расстояния, но если алгоритм не может обрабатывать отрицательные значения, это может стать проблемой. Вторая проблема заключается в том, что это сильно зависит от выбросов. Если одно наблюдение имеет очень экстремальное (высокое или низкое) значение измерения, нормализованное значение этого измерения для других наблюдений будет сгруппировано и потеряет свою способность различать.
Стандартная нормализация (z-масштабирование) нормализует измерение, чтобы оно имело 0 среднего и 1 стандартное отклонение, путем вычитания среднего из этого измерения каждого наблюдения и последующего деления на стандартное отклонение значения этого измерения по всем наблюдениям.
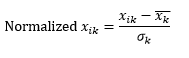
Это обычно удерживает данные в диапазоне от -5 до +5, грубо говоря, и позволяет избежать влияния экстремальных значений.
Мы смоделировали z-масштабирование двух наблюдений. Смоделировано, потому что нам действительно нужно гораздо больше, чем два наблюдения, чтобы вычислить среднее значение и стандартное отклонение каждого измерения, и мы предполагали оба этих числа для каждого измерения здесь.

Затем рассчитайте расстояние…
Евклидово расстояние — также известное как расстояние «по прямой» — это кратчайшее расстояние в многомерном гиперпространстве между двумя точками. Вы знакомы с этим в 2D-плоскости или 3D-пространстве (это линия), но аналогичная концепция распространяется и на более высокие измерения. Евклидово расстояние между векторами в n-мерном пространстве вычисляется как
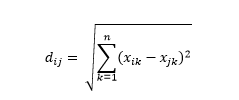
Для примеров преобразованного вектора данных это
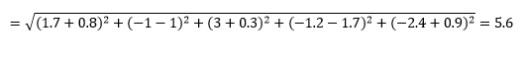
Это наиболее распространенная метрика, которая часто подходит для большинства приложений. Вариантом этого является квадратно-евклидово расстояние, которое представляет собой просто сумму квадратов разностей.
Манхэттенское расстояние , названное так из-за сетки Восток-Запад-Север-Юг, похожей на структуру улиц Манхэттена в Нью-Йорке, — это расстояние между двумя точками при движении параллельно осям.

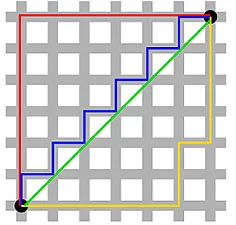
Манхэттен Расстояние
Евклидово расстояние
Это вычисляется как
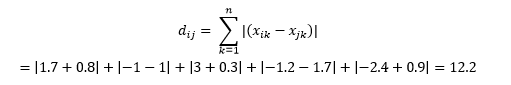
Это может быть полезно в некоторых приложениях, где расстояние используется в реальном, физическом смысле, а не в смысле «несходства» машинного обучения. Например, если вам нужно рассчитать расстояние, пройденное пожарной машиной, чтобы добраться до точки, то использование этого более практично.
Канберрское расстояние является взвешенным вариантом манхэттенского расстояния и рассчитывается как
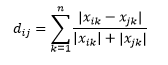
Расстояние L-нормы является расширением двух вышеперечисленных - или вы можете сказать, что два вышеперечисленных являются частными случаями расстояния L-нормы - и определяется как
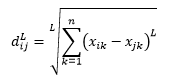
где L — целое положительное число. Я не сталкивался ни с одним случаем, когда мне нужно было использовать это, но это все еще полезно знать. Например, 3-нормовое расстояние будет
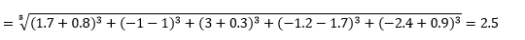
Обратите внимание, что L обычно должно быть четным целым числом, поскольку мы не хотим, чтобы положительные или отрицательные вклады расстояния компенсировались.
Расстояние Минковского является обобщением расстояния L-нормы, где L может принимать любое значение от 0 до включая дробные значения. Расстояние Минковского порядка p определяется как
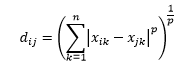

Косинусное расстояние — это мера угла между двумя векторами, каждый из которых представляет два наблюдения и формируется путем присоединения точки данных к началу координат. Косинусное расстояние находится в диапазоне от 0 (точно такое же) до 1 (нет связи) и вычисляется как
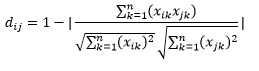
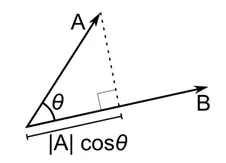
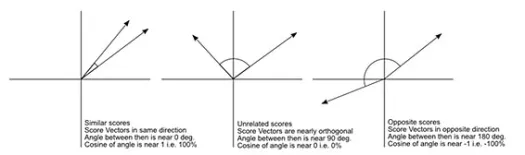
Хотя это более распространенная мера расстояния при работе с категориальными данными, ее также можно определить для числового вектора. Для наших числовых векторов это будет
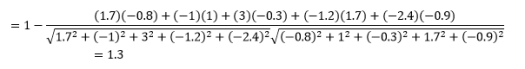
Но учтите предостережения…
Вы знали, что это произойдет, не так ли? Если бы аналитика была просто набором математических формул, нам не нужны были бы такие умные люди, как вы.
Первое, что нужно отметить, это то, что расстояния, рассчитанные по разным метрикам, различны. У вас может возникнуть соблазн подумать, что косинусное расстояние 1,3 является наименьшим и, следовательно, указывает на то, что векторы находятся ближе всего, но это неправильный способ интерпретации. Расстояния по разным методам нельзя сравнивать, и можно сравнивать только расстояния между разными парами наблюдений по одному и тому же методу. Расстояния имеют относительное значение и не имеют абсолютного значения сами по себе .
Это приводит к следующему вопросу о том, как выбрать правильную метрику расстояния. К сожалению, верного ответа нет. В зависимости от типа данных, контекста, бизнес-задачи, приложения и метода обучения модели разные показатели дают разные результаты. Вам придется использовать суждение, делать предположения или тестировать производительность модели, чтобы выбрать правильную метрику .
Второе предостережение — это мое часто повторяемое о проклятии размерности. В более высоких измерениях расстояния ведут себя не так, как мы интуитивно думаем , и аналитик должен быть чрезвычайно осторожным при использовании любой метрики.
Третье предостережение касается отношения между расстояниями между тремя наблюдениями. Некоторые показатели поддерживают неравенство треугольника, а другие нет . Неравенство треугольника подразумевает, что из точки i в точку j всегда кратчайший путь напрямую, а не через промежуточную точку k. Математически,
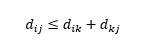
В зависимости от вашего приложения это может быть обязательным или необязательным свойством метрики расстояния.
О, еще одно: «расстояние» противоположно «сходству». Чем больше расстояние, тем меньше сходство и наоборот. Алгоритмы кластеризации работают на расстояниях, а алгоритмы рекомендаций работают на сходстве, но по сути они говорят об одном и том же.
Итак, как вы можете преобразовать число расстояния в число подобия?
