คำสาปแห่งมิติ
เผยแพร่แล้ว: 2015-07-08คำสาปแห่งมิติคืออะไร
Curse of Dimensionality หมายถึงคุณสมบัติที่ไม่เป็นธรรมชาติของข้อมูลที่สังเกตได้เมื่อทำงานในพื้นที่มิติสูง* ซึ่งเกี่ยวข้องกับการใช้งานและการตีความระยะทางและปริมาตรโดยเฉพาะ นี่เป็นหนึ่งในหัวข้อที่ฉันโปรดปรานในการเรียนรู้ของเครื่องและสถิติ เนื่องจากมีแอปพลิเคชันที่กว้างขวาง (ไม่เฉพาะเจาะจงสำหรับวิธีการเรียนรู้ด้วยเครื่องใด ๆ ) มันใช้งานง่ายมากและด้วยเหตุนี้จึงน่าเกรงขาม มีแอปพลิเคชันที่ลึกซึ้งสำหรับเทคนิคการวิเคราะห์ใด ๆ และ มีชื่อน่ากลัว 'เจ๋ง' เหมือนคำสาปอียิปต์!
เพื่อให้เข้าใจอย่างรวดเร็ว ให้พิจารณาตัวอย่างนี้: สมมติว่าคุณทำเหรียญตกบนเส้น 100 เมตร คุณจะพบมันได้อย่างไร? ง่ายๆ แค่เดินต่อแถวแล้วค้นหา แต่ถ้าเป็น 100 x 100 ตร.ม. สนาม? มันเริ่มยากขึ้นแล้ว พยายามค้นหาสนามฟุตบอล (คร่าวๆ) เพื่อหาเหรียญเพียงเหรียญเดียว แต่ถ้าเป็นพื้นที่ 100 x 100 x 100 ลบ.ม.ล่ะ! คุณรู้ไหม สนามฟุตบอลตอนนี้มีความสูงสามสิบชั้น ขอให้โชคดีในการหาเหรียญที่นั่น! แท้จริงแล้วคือ "คำสาปแห่งมิติ"
วิธีการ ML จำนวนมากใช้การวัดระยะทาง
วิธี การแบ่งส่วน และ จัดกลุ่ม ส่วนใหญ่อาศัยระยะทางในการคำนวณระหว่างการสังเกต การแบ่งส่วน k-Means ที่รู้จักกันดีจะกำหนดคะแนนไปยังศูนย์กลาง ที่ใกล้ที่สุด การจัดกลุ่ม DBSCAN และลำดับชั้นยังต้องการการวัดระยะทางด้วย อัลกอริธึม การตรวจจับค่าผิดปกติ ที่อิงตามการกระจายและความหนาแน่นยังใช้ประโยชน์จากระยะทางที่สัมพันธ์กับระยะทางอื่นๆ เพื่อทำเครื่องหมายค่าผิดปกติ
โซลูชันการจัดหมวดหมู่ภายใต้การดูแล เช่น วิธี k-Nearest Neighbors ยังใช้ระยะห่างระหว่างการสังเกตเพื่อกำหนดคลาสให้กับการสังเกตที่ไม่รู้จัก วิธี การสนับสนุน Vector Machine เกี่ยวข้องกับการเปลี่ยนการสังเกตรอบๆ เคอร์เนลที่เลือกตามระยะห่างระหว่างการสังเกตและเคอร์เนล
รูปแบบทั่วไปของ ระบบการแนะนำ เกี่ยวข้องกับความคล้ายคลึงกันตามระยะทางระหว่างเวกเตอร์แอตทริบิวต์ผู้ใช้และรายการ แม้ว่าจะใช้ระยะทางรูปแบบอื่นก็ตาม จำนวนมิติก็มีบทบาทในการออกแบบการวิเคราะห์
เมตริกระยะทางที่พบบ่อยที่สุดคือเมตริก Euclidian Distance ซึ่งเป็นระยะห่างเชิงเส้นง่ายๆ ระหว่างจุดสองจุดในไฮเปอร์สเปซหลายมิติ ระยะทางแบบยุคลิเดียนสำหรับจุด i และจุด j ในปริภูมิมิติ n สามารถคำนวณได้ดังนี้
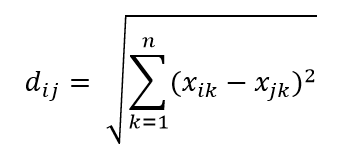
ระยะทางทำให้เกิดความหายนะในมิติสูง
พิจารณากระบวนการสุ่มตัวอย่างข้อมูลอย่างง่าย สมมติว่ากล่องสีดำด้านนอกในรูปที่ 1 คือ data Universe ที่มีการกระจายจุดข้อมูลอย่างสม่ำเสมอทั่วทั้งปริมาตร และเราต้องการสุ่มตัวอย่าง 1% ของการสังเกตที่ล้อมรอบด้วยกล่องสีแดงด้านใน กล่องดำคือไฮเปอร์คิวบ์ในพื้นที่หลายมิติ โดยแต่ละด้านแสดงถึงช่วงของค่าในมิตินั้น สำหรับตัวอย่าง 3 มิติอย่างง่ายในรูปที่ 1 เราอาจมีช่วงต่อไปนี้:
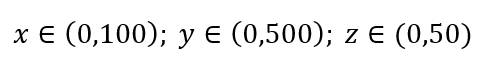
รูปที่ 1 : การสุ่มตัวอย่าง
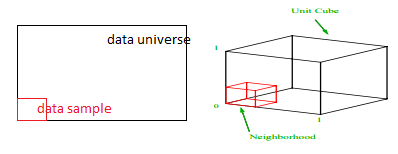
สัดส่วนของแต่ละช่วงที่เราควรสุ่มตัวอย่างเพื่อให้ได้ตัวอย่าง 1% คืออะไร? สำหรับ 2 มิติ 10% ของช่วงจะบรรลุการสุ่มตัวอย่าง 1% โดยรวม ดังนั้นเราอาจเลือก x∈(0,10) และ y∈(0,50) และคาดว่าจะได้ 1% ของการสังเกตทั้งหมด นี่เป็นเพราะ 10%2=1% คุณคาดว่าสัดส่วนนี้จะสูงหรือต่ำกว่าสำหรับสามมิติ?
แม้ว่าการค้นหาของเราจะอยู่ในทิศทางเพิ่มเติม แต่ตามสัดส่วนจริง ๆ แล้วเพิ่มขึ้นเป็น 21.5% และไม่เพียงเพิ่มขึ้นเท่านั้น แต่ยังเพิ่มเป็นสองเท่าอีกด้วย! และคุณจะเห็นได้ว่าเราต้องครอบคลุมเกือบหนึ่งในห้าของแต่ละมิติเพื่อให้ได้รวมหนึ่งร้อย! ใน 10 มิติ สัดส่วนนี้คือ 63% และใน 100 มิติ ซึ่งไม่ใช่จำนวนมิติที่ผิดปกติในแมชชีนเลิร์นนิงในชีวิตจริง เราต้องสุ่มตัวอย่างช่วง 95% ตามแต่ละมิติเพื่อสุ่มตัวอย่าง 1% ของการสังเกต! ผลลัพธ์ที่น่าเหลือเชื่อนี้เกิดขึ้นเนื่องจากการแพร่กระจายของจุดข้อมูลในมิติสูงจะมีขนาดใหญ่ขึ้น แม้ว่าจะมีการกระจายอย่างสม่ำเสมอ

ซึ่งมีผลในแง่ของการออกแบบการทดลองและการสุ่มตัวอย่าง กระบวนการมีราคาแพงมากในการคำนวณ แม้จะอยู่ในขอบเขตที่การสุ่มตัวอย่างเข้าใกล้ประชากรแม้ว่าขนาดตัวอย่างจะยังเล็กกว่าประชากรมากก็ตาม
พิจารณาผลที่ตามมาอีกประการหนึ่งของการมีมิติสูง อัลกอริธึมจำนวนมากวัดระยะทางระหว่างจุดข้อมูลสองจุดเพื่อกำหนดความ ใกล้เคียง บางประเภท (DBSCAN, Kernels, k-Nearest Neighbour) โดยอ้างอิงถึงเกณฑ์ระยะทางที่กำหนดไว้ล่วงหน้า ใน 2 มิติ เราสามารถจินตนาการได้ว่าจุดสองจุดอยู่ใกล้กัน หากจุดหนึ่งอยู่ในรัศมีที่กำหนดของอีกจุดหนึ่ง พิจารณาภาพซ้ายในรูปที่ 2 จุดที่มีระยะห่างเท่ากันภายในสี่เหลี่ยมสีดำอยู่ภายในวงกลมสีแดงคืออะไร? ที่เกี่ยวกับ
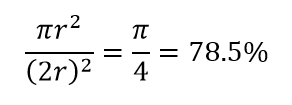
รูปที่ 2: ความใกล้ชิด
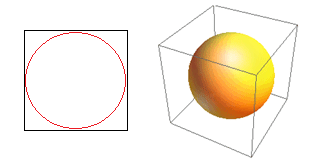
ดังนั้น หากคุณใส่วงกลมที่ใหญ่ที่สุดเท่าที่จะเป็นไปได้ภายในสี่เหลี่ยมจัตุรัส คุณจะครอบคลุม 78% ของสี่เหลี่ยมจัตุรัส ทว่าทรงกลมที่ใหญ่ที่สุดที่เป็นไปได้ภายในลูกบาศก์เท่านั้น
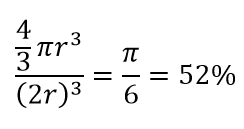
ของปริมาณ ปริมาณนี้ลดลงแบบทวีคูณเป็น 0.24% เพียง 10 มิติ! ความหมายโดยพื้นฐานแล้วในโลกที่มีมิติสูงทุกจุดข้อมูลอยู่ที่มุมและไม่มีอะไรเป็นศูนย์กลางของปริมาตรหรือกล่าวอีกนัยหนึ่งคือปริมาณศูนย์กลางลดลงจนไม่มีเลยเพราะเกือบจะไม่มีศูนย์กลาง! สิ่งนี้มีผลกระทบอย่างมากต่ออัลกอริธึมการจัดกลุ่มตามระยะทาง ระยะทางทั้งหมดเริ่มดูเหมือนเท่ากันและระยะทางใด ๆ ที่มากหรือน้อยกว่าอื่น ๆ นั้นเป็นความผันผวนของข้อมูลแบบสุ่มมากกว่าการวัดความไม่คล้ายคลึงใด ๆ!
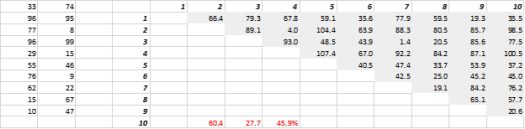
รูปที่ 3 แสดงข้อมูล 2 มิติที่สร้างแบบสุ่มและระยะทางทั้งหมดที่เกี่ยวข้อง ค่าสัมประสิทธิ์ความแปรปรวนในระยะทาง คำนวณเป็นค่าเบี่ยงเบนมาตรฐานหารด้วยค่าเฉลี่ย คือ 45.9% จำนวนที่สอดคล้องกันของข้อมูล 5-D ที่สร้างขึ้นในทำนองเดียวกันคือ 26.5% และสำหรับ 10-D คือ 19.1% เป็นที่ยอมรับว่านี่เป็นเพียงตัวอย่างหนึ่ง แต่เทรนด์สนับสนุนข้อสรุปที่ว่าในมิติสูงทุกระยะมีความใกล้เคียงกัน และไม่มีใครอยู่ใกล้หรือไกล!
รูปที่ 3: การจัดกลุ่มระยะทาง
มิติสูงก็มีผลกับอย่างอื่นด้วย
นอกจากระยะทางและปริมาตรแล้ว จำนวนมิติยังสร้างปัญหาในทางปฏิบัติอื่นๆ ข้อกำหนดรันไทม์ของโซลูชันและหน่วยความจำระบบมักจะเพิ่มขึ้นแบบไม่เชิงเส้นตามจำนวนมิติที่เพิ่มขึ้น เนื่องจากการเพิ่มขึ้นแบบทวีคูณในโซลูชันที่เป็นไปได้ วิธีการเพิ่มประสิทธิภาพจำนวนมากไม่สามารถเข้าถึงการเพิ่มประสิทธิภาพระดับโลกและต้องดำเนินการกับการปรับให้เหมาะสมในพื้นที่ นอกจากนี้ แทนที่จะใช้โซลูชันแบบปิด การเพิ่มประสิทธิภาพต้องใช้อัลกอริธึมตามการค้นหา เช่น การไล่ระดับสี อัลกอริทึมทางพันธุกรรม และการหลอมจำลอง มิติที่มากขึ้นทำให้เกิดความเป็นไปได้ของความสัมพันธ์และการประมาณค่าพารามิเตอร์อาจกลายเป็นเรื่องยากในแนวทางการถดถอย
รับมือกับมิติสูง
นี่จะเป็นการโพสต์บล็อกที่แยกจากกันในตัวเอง แต่การวิเคราะห์สหสัมพันธ์ การจัดกลุ่ม ค่าข้อมูล ปัจจัยเงินเฟ้อความแปรปรวน การวิเคราะห์องค์ประกอบหลักเป็นวิธีการบางส่วนที่สามารถลดจำนวนมิติข้อมูลได้
* จำนวนตัวแปร การสังเกต หรือคุณลักษณะที่จุดข้อมูลประกอบขึ้นเรียกว่า มิติข้อมูล ตัวอย่างเช่น จุดใดๆ ในอวกาศสามารถแสดงโดยใช้พิกัดความยาว ความกว้าง และความสูง 3 พิกัด และมี 3 มิติ
