การประมาณความหนาแน่นโดยใช้ฮิสโตแกรม

ฟังก์ชันความหนาแน่นของความน่าจะเป็น (PDF) อธิบายความน่าจะเป็นของการสังเกตตัวแปรสุ่มอย่างต่อเนื่องบางตัวในพื้นที่บางส่วนของพื้นที่ สำหรับตัวแปรสุ่มหนึ่งมิติ X ให้จำไว้ว่า PDF f(x) เป็นไปตามคุณสมบัติที่

ความน่าจะเป็นที่ตัวแปรรับค่าระหว่าง

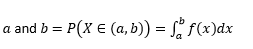
ความน่าจะเป็นที่ตัวแปรรับค่าเท่ากับ

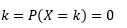
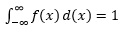
การประมาณค่า PDF จากตัวอย่างข้อสังเกตเป็นปัญหาทั่วไปในการเรียนรู้ของเครื่อง สิ่งนี้มีประโยชน์ในอัลกอริธึมการตรวจจับค่าผิดปกติจำนวนมากที่เราพยายามประเมินการกระจาย "จริง" ตามการสังเกตตัวอย่าง แล้วจัดประเภทการสังเกตที่มีอยู่หรือใหม่บางส่วนเป็นค่าผิดปกติหรือไม่ ตัวอย่างเช่น บริษัทประกันภัยรถยนต์ที่สนใจจับการฉ้อโกงอาจตรวจสอบคำขอจำนวนเงินค่าสินไหมทดแทนสำหรับงานตัวถังแต่ละประเภท เช่น การเปลี่ยนบัมเปอร์ และทำเครื่องหมายการฉ้อโกงที่อาจเกิดขึ้นในจำนวนเงินที่สูงเกินไป ในอีกตัวอย่างหนึ่ง นักจิตวิทยาเด็กอาจตรวจสอบเวลาที่ใช้ในการทำงานที่กำหนดในเด็กที่แตกต่างกัน และทำเครื่องหมายว่าเด็กเหล่านั้นใช้เวลานานเกินไปหรือสั้นเกินไปสำหรับการสืบสวนที่อาจเกิดขึ้น

ในบล็อกโพสต์นี้ เราจะพูดถึงวิธีที่เราสามารถ เรียนรู้ PDF จากตัวอย่างการสังเกต เพื่อให้เราสามารถคำนวณความน่าจะเป็นสำหรับการสังเกตแต่ละครั้ง และตัดสินใจว่าเป็นเรื่องปกติหรือเกิดขึ้นได้ยาก

การประมาณความหนาแน่นโดยใช้ฮิสโตแกรม

ขั้นแรก เราสร้างข้อมูลสุ่มสำหรับการสาธิต

set.seed(123)
data <- c(rnorm(200, 10, 20), rnorm(200, 60, 30), runif(200, 120, 180)) # 600 points

ต่อไป เราเห็นภาพเหล่านี้เพื่อความเข้าใจ โดยใช้ฮิสโตแกรมดังในรูปที่ 1

# Plot 1
hist(data, breaks=50, freq=F, main="Univariate Distribution", xlab="Data Value")
# Plot 2
hist(data, breaks=20, freq=F, main="", xlab="20 Data Bins", col='red', border='red')
par(new=T)
hist(data, breaks=100, freq=F, main="Univariate Distribution", xlab=NULL, xaxt='n', yaxt='n')

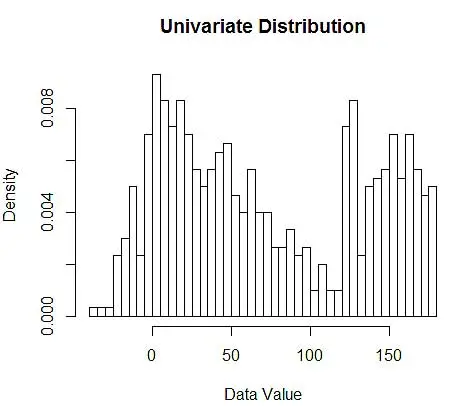
แม้ว่าฮิสโตแกรมเป็นแผนภูมิสำหรับการแสดงข้อมูลเป็นภาพ คุณยังสามารถเห็นได้ด้วยว่าเป็นค่าประมาณความหนาแน่นครั้งแรกของเรา โดยเฉพาะอย่างยิ่ง เราสามารถ ประมาณความหนาแน่นโดยการแบ่งข้อมูลออกเป็นถังขยะ และสมมติว่าความหนาแน่นคงที่ภายในช่วงของถังขยะนั้น และมีค่าเท่ากับจำนวนการสังเกตที่ตกลงไปในถังขยะนั้นตามสัดส่วนของจำนวนการสังเกตทั้งหมด

ดังนั้น PDF โดยประมาณคือ

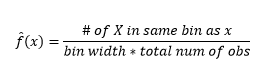
และคุณตระหนักว่าคุณได้ตั้งสมมติฐานเกี่ยวกับ bin-width ซึ่งจะส่งผลต่อการประมาณความหนาแน่น ดังนั้น bin-width จึงเป็นพารามิเตอร์สำหรับโมเดลการประมาณความหนาแน่นโดยใช้ฮิสโตแกรม อย่างไรก็ตาม ข้อเท็จจริงที่ถูกมองข้ามก็คือ เรากำลังทำงานกับพารามิเตอร์อีกหนึ่งตัว ซึ่งเป็น ตำแหน่งเริ่มต้นของ bin แรก คุณสามารถดูได้ว่าการเปลี่ยนแปลงดังกล่าวอาจส่งผลต่อการประมาณความหนาแน่นของถังขยะทั้งหมดอย่างไร หากต้องการดูผลกระทบของ bin-width รูปที่ 2 จะซ้อนทับค่าประมาณความหนาแน่นด้วยฮิสโทแกรม 20-bin และ 100-bin ดูที่บริเวณที่ล้อมรอบ ซึ่งถังขยะจำนวนน้อย/หยาบกว่าจะให้ค่าประมาณความหนาแน่นแบบเรียบ ในขณะที่ถังจำนวนมาก/ละเอียดกว่านั้นให้ค่าประมาณความหนาแน่นที่แตกต่างกัน สำหรับจุดสีเหลือง การประมาณความหนาแน่นจะอยู่ในช่วง 0.004 ถึง 0.008 จากสองรุ่นที่แตกต่างกัน

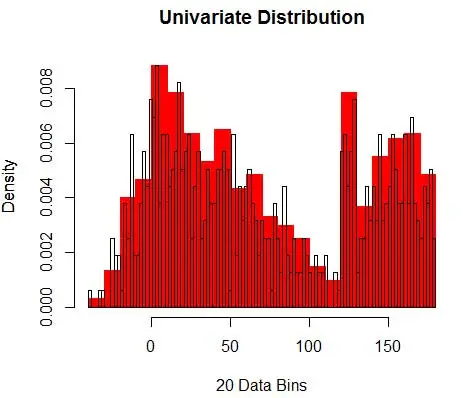
ดังนั้น การเลือกพารามิเตอร์ที่เหมาะสมจึงมีความสำคัญอย่างยิ่งต่อการประมาณความหนาแน่นอย่างถูกต้อง เราจะไปถึงจุดนั้น แต่โปรดทราบว่ายังมีปัญหาอื่นๆ เกี่ยวกับฮิสโตแกรมอีกด้วย การประมาณความหนาแน่นโดยใช้ฮิสโตแกรมค่อนข้างกระตุกและไม่ต่อเนื่อง ความหนาแน่นจะคงที่สำหรับถังขยะ และทันใดนั้นก็เปลี่ยนแปลงอย่างมากสำหรับจุดที่อยู่นอกถังขยะเพียงเล็กน้อย ซึ่งจะทำให้ผลที่ตามมาของการประมาณการที่ไม่ถูกต้องเลวร้ายยิ่งกว่าเดิมสำหรับปัญหาในทางปฏิบัติ

สุดท้ายนี้ เราได้ทำงานกับตัวแปรมิติเดียวเพื่อให้ง่ายต่อการอธิบาย แต่ในทางปฏิบัติ ปัญหาส่วนใหญ่จะเป็นแบบหลายมิติ เนื่องจาก จำนวนถังขยะเพิ่มขึ้นแบบทวีคูณตามจำนวนมิติ จำนวนการสังเกตที่จำเป็นในการประมาณความหนาแน่นจึงเพิ่มขึ้น ด้วย ในความเป็นจริง เป็นไปได้ว่าถึงแม้จะมีการสังเกตนับล้านครั้ง แต่ถังขยะจำนวนมากยังคงว่างเปล่าหรือมีข้อสังเกตที่เป็นตัวเลขหลักเดียว ด้วยถังขยะเพียง 50 ถังใน 3 มิติ เรามี 503=125000 เซลล์ซึ่งจำเป็นต้องเติมข้อมูล นั่นคือค่าเฉลี่ยของการสังเกต 8 ครั้งต่อเซลล์ สมมติว่ามีการกระจายแบบสม่ำเสมอ ข้อมูลการฝึกการสังเกตนับล้านรายการ

วิธีการเลือกพารามิเตอร์ที่เหมาะสม?

สำหรับ bin-width n จำนวนการสังเกต N สำหรับ bin J สัดส่วนของการสังเกตคือ

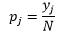
และการประมาณความหนาแน่นคือ

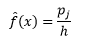
ทฤษฎีทางสถิติพิสูจน์ว่าในขณะที่ f(x) เป็นค่าความหนาแน่นที่คาดหวังในถังขยะ ความแปรปรวนของความหนาแน่นคือ

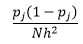
ในขณะที่เราสามารถประมาณความหนาแน่นได้ดีขึ้นโดยการลด bin-width n เราเพิ่มความแปรปรวนของการประมาณ เนื่องจากเราสามารถสัมผัสได้ถึงความกว้างของ bin-width ที่ละเอียดเกินไป เราสามารถใช้เทคนิคการตรวจสอบข้ามแบบปล่อยครั้งเดียวเพื่อประเมินชุดพารามิเตอร์ที่เหมาะสมที่สุด เราสามารถประมาณความหนาแน่นได้โดยใช้การสังเกตทั้งหมดแต่เพียงอย่างเดียว จากนั้นจึงคำนวณความหนาแน่นของการสังเกตที่ไม่ได้สังเกตและวัดข้อผิดพลาดในการประมาณค่า การแก้สมการทางคณิตศาสตร์สำหรับฮิสโตแกรมทำให้ได้โซลูชันแบบปิดสำหรับฟังก์ชันการสูญเสียสำหรับความกว้างช่องสัญญาณที่กำหนด

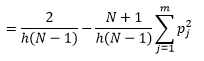
โดยที่ m คือจำนวนถังขยะ รายละเอียดทางเทคนิคข้างต้นอยู่ในการบรรยายนี้ [pdf] เราสามารถพลอตฟังก์ชันการสูญเสียนี้สำหรับถังขยะจำนวนต่างๆ ได้ (ภาพที่ 3)

getLoss <- function(n.break) {
N <- 600
res <- hist(data, breaks=n.break, freq=F)
bin <- as.numeric(res$breaks)
h <- bin[2]-bin[1]
p <- res$density
p <- p * h
return ( 2/(h*(N-1)) - ( (N+1)/(h*(N-1))*sum(p*p) ) )
}
loss.func <- data.frame(n=1:600)
loss.func$J <- sapply(loss.func$n, function(x) getLoss(x))
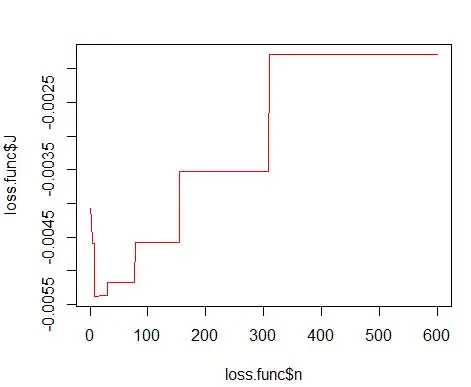
# Plot 3
plot(loss.func$n, loss.func$J, col='red', type='l')
opt.break <- max(loss.func[loss.func$J == min(loss.func$J), 'n'])
print(opt.break)
# Plot 4
hist(data, breaks=opt.break, freq=F, main="Univariate Distribution", xlab="15 Data Bins")

และรับจำนวนที่เหมาะสมที่สุดเป็น 15 จริงๆ แล้ว 8-15 ก็ใช้ได้

ดังนั้น ด้านล่างรูปที่ 4 คือการประมาณความหนาแน่นซึ่งปรับสมดุลค่าความหนาแน่นและความละเอียดอย่างละเอียด (ด้วยการแลกเปลี่ยนความแปรปรวนอคติที่เหมาะสมที่สุด)

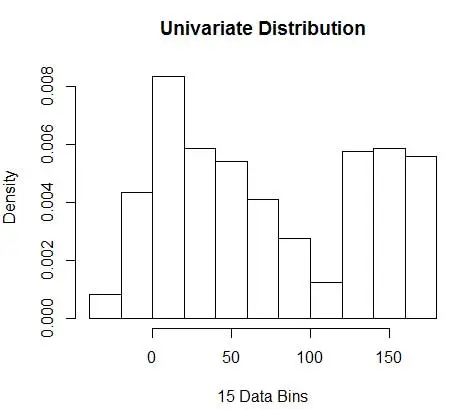
หากคุณรู้สึกไม่สบายใจเล็กน้อย ณ จุดนี้ ฉันจะอยู่กับคุณ แม้ว่าจำนวนถังขยะจะเหมาะสมที่สุดทางคณิตศาสตร์ แต่ก็รู้สึกว่าเป็นการประมาณที่หยาบเกินไป ไม่มีความรู้สึกที่เข้าใจได้ง่ายว่าทำไมเราถึงได้ทำหน้าที่ได้ดีที่สุด และอย่าลืมข้อกังวลอื่นๆ เกี่ยวกับตำแหน่งเริ่มต้น การประมาณแบบไม่ต่อเนื่อง และการสาปแช่งของมิติ อย่าท้อแท้ มีวิธีที่ดีกว่า ในโพสต์ถัดไป เราจะพูดถึงการประมาณความหนาแน่นโดยใช้เคอร์เนล