การวัดระยะทางในไฮเปอร์สเปซ

ใครก็ตามที่คุ้นเคยกับเทคนิคการวิเคราะห์คร่าวๆ จะสังเกตเห็นอัลกอริธึมมากมายที่อาศัยระยะทางระหว่างจุดข้อมูลสำหรับแอปพลิเคชัน การสังเกตแต่ละครั้ง หรือตัวอย่างข้อมูล มักจะแสดงเป็นเวกเตอร์หลายมิติ และการป้อนข้อมูลไปยังอัลกอริทึมต้องใช้ระยะห่างระหว่างคู่ของการสังเกตดังกล่าวแต่ละคู่

วิธีการคำนวณระยะทางขึ้นอยู่กับประเภทของข้อมูล – ตัวเลข การจัดหมวดหมู่ หรือแบบผสม อัลกอริธึมบางตัวใช้กับการสังเกตประเภทเดียวเท่านั้น ในขณะที่บางอัลกอริทึมทำงานหลายแบบ ในโพสต์นี้ เราจะพูดถึงการวัดระยะทางที่ใช้กับข้อมูลตัวเลข อาจมีหลายวิธีที่สามารถวัดระยะทางในไฮเปอร์สเปซหลายมิติได้มากกว่าที่จะครอบคลุมในโพสต์บล็อกเดียว และสามารถคิดค้นวิธีการใหม่ ๆ ได้เสมอ แต่เราพิจารณาเมตริกระยะทางทั่วไปบางส่วนและข้อดีที่เกี่ยวข้อง

เพื่อจุดประสงค์ในส่วนที่เหลือของโพสต์บล็อก เราหมายถึง

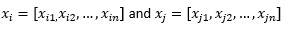
เพื่ออ้างถึงสองข้อสังเกตหรือเวกเตอร์ข้อมูล

เตรียมข้อมูลให้พร้อมก่อน...

ก่อนที่เราจะตรวจสอบการวัดระยะทางต่างๆ เราต้องเตรียมข้อมูล:

การแปลงเป็นเวกเตอร์ตัวเลข

สำหรับการสังเกตแบบผสมซึ่งมีทั้งมิติเชิงตัวเลขและเชิงหมวดหมู่ ขั้นตอนแรกคือการแปลงมิติเชิงหมวดหมู่เป็นมิติเชิงตัวเลขจริง ๆ มิติเชิงหมวดหมู่ที่มีค่าที่เป็นไปได้สามค่าสามารถเปลี่ยนเป็นมิติตัวเลขสองหรือสามค่าด้วยค่าไบนารี เนื่องจากตัวแปรตามหมวดหมู่นี้จำเป็นต้องใช้ค่าหนึ่งในสามค่า ดังนั้นมิติข้อมูลตัวเลขหนึ่งในสามจะมีความสัมพันธ์อย่างสมบูรณ์กับอีกสองค่า สิ่งนี้อาจจะใช่หรือไม่ก็ได้ขึ้นอยู่กับใบสมัครของคุณ

หากการสังเกตเป็นหมวดหมู่อย่างหมดจด เช่น สตริงข้อความ (ประโยคความยาวต่างกัน) หรือลำดับจีโนม (ลำดับความยาวคงที่) เมตริกระยะทางพิเศษบางรายการก็สามารถนำมาใช้โดยตรงโดยไม่ต้องแปลงข้อมูลเป็นรูปแบบตัวเลข เราจะพูดถึงอัลกอริทึมเหล่านี้ในโพสต์ถัดไป

การทำให้เป็นมาตรฐาน

ขึ้นอยู่กับกรณีการใช้งานของคุณ คุณอาจต้องการทำให้แต่ละมิติเป็นปกติในมาตราส่วนเดียวกัน เพื่อให้ระยะห่างตามมิติใดมิติหนึ่งไม่ส่งผลต่อระยะห่างโดยรวมระหว่างการสังเกตอย่างเกินควร สิ่งเดียวกันถูกกล่าวถึงในอัลกอริธึม k-Means การทำให้เป็นมาตรฐานเป็นไปได้สองประเภท:

การทำให้เป็นมาตรฐานของ ช่วง (การปรับขนาด) ทำให้ข้อมูลเป็นปกติในช่วง 0-1 โดยการลบค่าต่ำสุดออกจากแต่ละส่วนข้อมูล แล้วหารด้วยช่วงของค่าในมิตินั้น

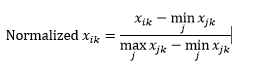
ปัญหาแรกกับการทำให้ช่วงเป็นมาตรฐานคือค่าที่มองไม่เห็นอาจถูกทำให้เป็นมาตรฐานเกินช่วง 0-1 แม้ว่าโดยทั่วไปจะไม่เป็นปัญหาสำหรับเมตริกระยะทางส่วนใหญ่ แต่ถ้าอัลกอริทึมไม่สามารถจัดการค่าลบได้ ก็อาจเป็นปัญหาได้ ปัญหาที่สองคือสิ่งนี้ขึ้นอยู่กับค่าผิดปกติอย่างมาก หากการสังเกตหนึ่งมีค่ามาก (สูงหรือต่ำ) สำหรับมิติหนึ่ง ค่ามาตรฐานสำหรับมิตินั้นสำหรับการสังเกตอื่น ๆ จะถูกรวมเข้าด้วยกันและสูญเสียอำนาจการเลือกปฏิบัติ

การทำให้เป็นมาตรฐานมาตรฐาน (z-scaling) ทำให้มิติปกติมีค่าเฉลี่ย 0 และ 1 ส่วนเบี่ยงเบนมาตรฐานโดยลบค่าเฉลี่ยออกจากมิตินั้นของการสังเกตแต่ละครั้งแล้วหารด้วยค่าเบี่ยงเบนมาตรฐานของค่าของมิตินั้นจากการสังเกตทั้งหมด

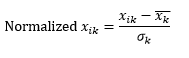
โดยทั่วไปจะเก็บข้อมูลในช่วง -5 ถึง +5 โดยประมาณ และหลีกเลี่ยงอิทธิพลของค่าสุดขีด

เราได้จำลองการปรับขนาด z ของการสังเกตสองครั้ง จำลองขึ้น เนื่องจากเราต้องการการสังเกตมากกว่าสองครั้งจริงๆ เพื่อคำนวณค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของแต่ละมิติ และเราได้สันนิษฐานว่าทั้งสองจำนวนนี้สำหรับแต่ละมิติ

แล้วคำนวณระยะทาง...

ระยะทางแบบยุคลิดหรือที่รู้จักกันว่าระยะทาง "ในขณะที่อีกาบิน" คือระยะทางที่สั้นที่สุดในไฮเปอร์สเปซหลายมิติระหว่างจุดสองจุด คุณคุ้นเคยกับสิ่งนี้ในระนาบ 2 มิติหรือพื้นที่ 3 มิติ (นี่คือเส้น) แต่แนวคิดที่คล้ายกันขยายไปสู่มิติที่สูงกว่า ระยะห่างแบบยุคลิดระหว่างเวกเตอร์ในปริภูมิ n มิติคำนวณเป็น

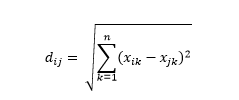
สำหรับตัวอย่างเวกเตอร์ข้อมูลที่แปลงแล้ว นี่คือ

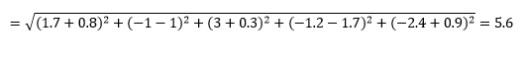
นี่เป็นเมตริกทั่วไปและมักเหมาะสำหรับการใช้งานส่วนใหญ่ ตัวแปรนี้คือระยะทางกำลังสอง-ยุคลิด ซึ่งเป็นเพียงผลรวมของผลต่างกำลังสอง

ระยะทางแมนฮัตตัน - ตั้งชื่อตามตารางตะวันออก - ตะวันตก - เหนือ - ใต้เช่นโครงสร้างของถนนในแมนฮัตตันในนิวยอร์ก - คือระยะห่างระหว่างจุดสองจุดเมื่อข้ามขนานกับแกน

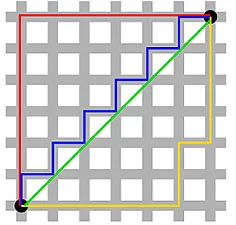
ระยะทางแมนฮัตตัน
ระยะทางแบบยุคลิด

นี่คำนวณเป็น

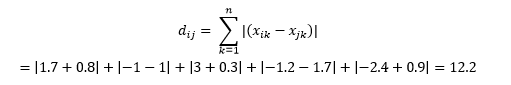
นี้อาจมีประโยชน์ในบางแอปพลิเคชันที่ใช้ระยะทางในความรู้สึกทางกายภาพที่แท้จริง มากกว่าความรู้สึกของ "ความแตกต่าง" ของแมชชีนเลิร์นนิง ตัวอย่างเช่น หากคุณต้องการคำนวณระยะทางที่รถดับเพลิงใช้เพื่อไปถึงจุดหนึ่ง การใช้วิธีนี้จะเป็นประโยชน์มากกว่า

ระยะทางแคนเบอร์รา เป็นการถ่วงน้ำหนักของระยะทางแมนฮัตตัน และคำนวณเป็น

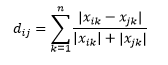
L-norm distance คือส่วนขยายที่สูงกว่า 2 – หรือคุณอาจพูดได้ว่า 2 ข้างบนนั้นเป็นกรณีเฉพาะของ L-norm distance – และถูกกำหนดเป็น

โดยที่ L เป็นจำนวนเต็มบวก ฉันไม่เคยเจอกรณีใด ๆ ที่ฉันจำเป็นต้องใช้สิ่งนี้ แต่ก็ยังดีที่จะรู้ถึงความเป็นไปได้ ตัวอย่างเช่น ระยะทาง 3-norm จะเป็น

โปรดทราบว่าโดยทั่วไปแล้ว L ควรเป็นจำนวนเต็มคู่ เนื่องจากเราไม่ต้องการให้การบริจาคระยะทางบวกหรือลบยกเลิก

ระยะทาง Minkowski เป็นลักษณะทั่วไปของระยะทาง L-norm โดยที่ L สามารถนำค่าใดก็ได้จาก 0 ไปรวมค่าเศษส่วน Minkowski ระยะทางของคำสั่ง p ถูกกำหนดเป็น

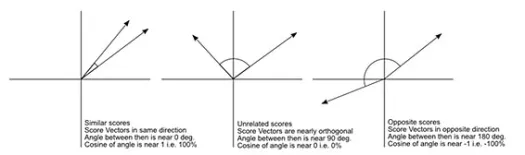
ระยะทางโคไซน์ คือการวัดมุมระหว่างเวกเตอร์สองตัว แต่ละเวกเตอร์แทนการสังเกตสองครั้ง และเกิดขึ้นจากการรวมจุดข้อมูลไปยังจุดกำเนิด ระยะทางโคไซน์มีตั้งแต่ 0 (เหมือนกันทุกประการ) ถึง 1 (ไม่มีการเชื่อมต่อ) และคำนวณเป็น

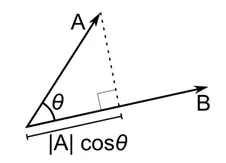
แม้ว่านี่จะเป็นการวัดระยะทางทั่วไปมากกว่าเมื่อทำงานกับข้อมูลที่เป็นหมวดหมู่ แต่ก็สามารถกำหนดสิ่งนี้สำหรับเวกเตอร์ตัวเลขได้ สำหรับเวกเตอร์ตัวเลขของเรา นี่จะเป็น

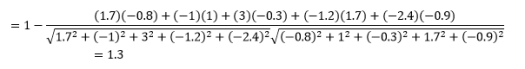
แต่ระวังคำเตือน...

คุณรู้ว่าสิ่งนี้กำลังมาใช่ไหม หากการวิเคราะห์เป็นเพียงสูตรทางคณิตศาสตร์จำนวนมาก เราก็ไม่ต้องการคนฉลาดเช่นคุณ

สิ่งแรกที่ควรทราบคือระยะทางที่คำนวณโดยเมตริกต่างๆ นั้นแตกต่างกัน คุณอาจถูกล่อลวงให้คิดว่าระยะทางโคไซน์ที่ 1.3 นั้นเล็กที่สุดและด้วยเหตุนี้จึงบ่งชี้ว่าเวกเตอร์อยู่ใกล้ที่สุด แต่นี่ไม่ใช่วิธีการตีความที่ถูกต้อง ไม่สามารถเปรียบเทียบระยะทางระหว่างวิธีการต่างๆ ได้ และสามารถเปรียบเทียบได้เฉพาะระยะทางระหว่างคู่ของการสังเกตที่ต่างกันภายใต้วิธีการเดียวกันเท่านั้น ระยะทางมีความหมายสัมพัทธ์และไม่มีความหมายที่แน่นอนในตัวเอง

สิ่งนี้นำไปสู่คำถามถัดไปเกี่ยวกับวิธีเลือกเมตริกระยะทางที่เหมาะสม น่าเสียดายที่ไม่มีคำตอบที่แท้จริง ขึ้นอยู่กับประเภทของข้อมูล บริบท ปัญหาทางธุรกิจ แอปพลิเคชัน และวิธีการฝึกอบรมแบบจำลอง ตัวชี้วัดที่แตกต่างกันให้ผลลัพธ์ที่แตกต่างกัน คุณจะต้องใช้วิจารณญาณ ตั้งสมมติฐาน หรือทดสอบประสิทธิภาพของแบบจำลองเพื่อตัดสินใจเลือกเมตริกที่ถูกต้อง

ข้อแม้ประการที่สองคือคำสาปแห่งมิติที่ฉันพูดซ้ำบ่อยๆ ในมิติที่สูงกว่า ระยะทางจะไม่เป็นไปตามที่เราคิดโดยสัญชาตญาณ และนักวิเคราะห์จะต้องระมัดระวังอย่างยิ่งเมื่อใช้เมตริกใดๆ

ข้อแม้ที่สามเป็นเรื่องเกี่ยวกับความสัมพันธ์ระหว่างระยะทางระหว่างสามข้อสังเกต ตัวชี้วัดบางตัวสนับสนุนความไม่เท่าเทียมกันของสามเหลี่ยม และในขณะที่บางตัวไม่รองรับ ความไม่เท่าเทียมกันของสามเหลี่ยมบอกเป็นนัยว่ามันสั้นที่สุดเสมอที่จะไปจากจุด i ไปยังจุด j โดยตรง แทนที่จะผ่านจุดตรงกลาง k ทางคณิตศาสตร์

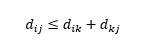
ขึ้นอยู่กับใบสมัครของคุณ คุณสมบัตินี้อาจจำเป็นหรือไม่จำเป็นของการวัดระยะทาง

อ้อ อีกอย่าง "ระยะทาง" ตรงข้ามกับ "ความคล้ายคลึง" ระยะห่างที่สูงขึ้น ลดความคล้ายคลึงกัน และในทางกลับกัน อัลกอริธึมการจัดกลุ่มทำงานในระยะทาง และอัลกอริธึมการแนะนำทำงานบนความคล้ายคลึงกัน แต่โดยพื้นฐานแล้วมันกำลังพูดถึงสิ่งเดียวกัน

แล้วจะแปลงเลขระยะทางเป็นเลขความเหมือนได้อย่างไร