Boyutluluk Laneti
Yayınlanan: 2015-07-08Boyutluluğun Laneti Nedir?
Boyutluluğun Laneti, özellikle uzaklıkların ve hacimlerin kullanılabilirliği ve yorumlanmasıyla ilgili olarak, yüksek boyutlu uzayda* çalışırken gözlemlenen verilerin sezgisel olmayan özelliklerini ifade eder. Bu, geniş uygulamaları olduğundan (herhangi bir makine öğrenimi yöntemine özgü olmadığından), çok sezgisel ve dolayısıyla hayranlık uyandırdığından, herhangi bir analitik tekniği için kapsamlı bir uygulamaya sahip olduğundan, Makine Öğrenimi ve İstatistikte en sevdiğim konulardan biridir ve Mısır laneti gibi 'havalı' korkunç bir adı var!
Hızlı bir şekilde kavramak için şu örneği düşünün: Diyelim ki 100 metrelik bir çizgiye bozuk para düşürdünüz. Bunu nasıl buluyorsun? Basit, sadece hatta yürüyün ve arayın. Ama ya 100 x 100 metrekare ise? alan? Tek bir jeton için (kabaca) bir futbol sahası aramaya çalışmak zaten zorlaşıyor. Ama ya 100 x 100 x 100 m2 boşluksa?! Biliyorsunuz, futbol sahası artık otuz kat yüksekliğe sahip. Orada bir madeni para bulmakta iyi şanslar! Bu, özünde “boyutluluğun laneti”dir.
Birçok ML yöntemi Mesafe Ölçümü kullanır
Çoğu segmentasyon ve kümeleme yöntemi, gözlemler arasındaki hesaplama mesafelerine dayanır. İyi bilinen k-Means segmentasyonu, noktaları en yakın merkeze atar. DBSCAN ve Hiyerarşik kümeleme de mesafe ölçümleri gerektiriyordu. Dağılım ve yoğunluğa dayalı aykırı değer algılama algoritmaları, aykırı değerleri işaretlemek için diğer mesafelere göre mesafeyi de kullanır.
K-En Yakın Komşular yöntemi gibi denetimli sınıflandırma çözümleri de, bilinmeyen gözleme sınıf atamak için gözlemler arasındaki mesafeyi kullanır. Destek Vektör Makinesi yöntemi, gözlem ve çekirdek arasındaki mesafeye dayalı olarak seçilen Çekirdekler etrafındaki gözlemleri dönüştürmeyi içerir.
Tavsiye sistemlerinin yaygın biçimi, kullanıcı ve öğe öznitelik vektörleri arasında mesafeye dayalı benzerliği içerir. Diğer mesafe biçimleri kullanılsa bile, analitik tasarımda boyutların sayısı bir rol oynar.
En yaygın mesafe metriklerinden biri, çok boyutlu hiper uzayda iki nokta arasındaki basit doğrusal mesafe olan Öklid Mesafe metriğidir. n boyutlu uzayda i noktası ve j noktası için Öklid Uzaklığı şu şekilde hesaplanabilir:
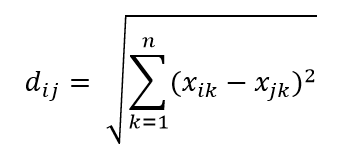
Mesafe yüksek boyutta ortalığı kasıp kavuruyor
Basit bir veri örnekleme sürecini düşünün. Şekil 1'deki siyah dış kutunun, tüm hacim boyunca veri noktalarının tek tip dağılımına sahip veri evreni olduğunu ve kırmızı iç kutuyla çevrelenen gözlemlerin %1'ini örneklemek istediğimizi varsayalım. Kara kutu, çok boyutlu uzayda, her bir kenarı o boyuttaki değer aralığını temsil eden hiper-küptür. Şekil 1'deki basit 3 boyutlu örnek için aşağıdaki aralığa sahip olabiliriz:
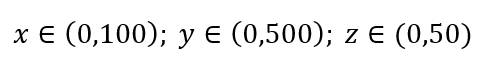
Şekil 1: Örnekleme
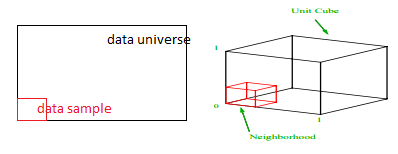
Bu %1'lik örneği elde etmek için her aralığın oranı nedir? 2 boyut için, aralığın %10'u toplam %1 örneklemeye ulaşacaktır, bu nedenle x∈(0,10) ve y∈(0,50)'yi seçebilir ve tüm gözlemlerin %1'ini yakalamayı bekleyebiliriz. Bunun nedeni %102=1% olmasıdır. Bu oranın 3 boyut için daha mı yüksek yoksa daha mı düşük olmasını bekliyorsunuz?
Aramamız şimdi ek yönde olsa da, orantı aslında %21.5'e çıkıyor. Ve sadece bir ek boyut için artmaz, ikiye katlanır! Ve genelin yüzde birini elde etmek için her boyutun neredeyse beşte birini kapsamamız gerektiğini görebilirsiniz! 10 boyutta, bu oran %63'tür ve 100 boyutta - ki bu gerçek hayattaki herhangi bir makine öğreniminde alışılmadık sayıda boyut değildir - gözlemlerin %1'ini örneklemek için her bir boyut boyunca aralığın %95'ini örneklemek gerekir! Bu akıllara durgunluk veren sonuç, çünkü yüksek boyutlarda veri noktalarının dağılımı, düzgün bir şekilde yayılmış olsalar bile daha büyük hale geliyor.

Bunun deney tasarımı ve örnekleme açısından sonuçları vardır. Örneklem büyüklüğü popülasyondan çok daha küçük kalmasına rağmen örnekleme asimptotik olarak popülasyona yaklaşsa bile süreç hesaplama açısından çok pahalı hale gelir.
Yüksek boyutluluğun başka bir büyük sonucunu düşünün. Birçok algoritma, önceden tanımlanmış bir mesafe eşiğine göre bir tür yakınlık ( DBSCAN , Çekirdekler, k-En Yakın Komşu) tanımlamak için iki veri noktası arasındaki mesafeyi ölçer. 2 boyutta, biri diğerinin belirli yarıçapı içindeyse, iki noktanın yakın olduğunu hayal edebiliriz. Şekil 2'deki soldaki resmi ele alalım. Kırmızı dairenin içindeki siyah karenin içindeki düzgün aralıklı noktaların payı nedir? hakkında
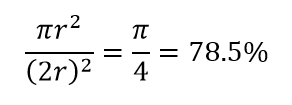
Şekil 2: Yakınlık
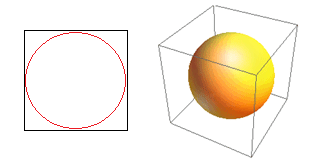
Yani mümkün olan en büyük daireyi karenin içine sığdırırsanız, karenin %78'ini kaplarsınız. Ancak, küpün içindeki mümkün olan en büyük küre yalnızca
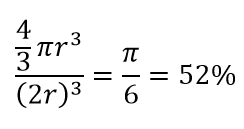
hacminin. Bu hacim, yalnızca 10 boyut için katlanarak %0,24'e düşer! Yüksek boyutlu dünyada her bir veri noktasının köşelerde olduğu ve hiçbir şeyin gerçekten hacmin merkezi olmadığı veya başka bir deyişle, merkez hacminin (neredeyse) merkez olmadığı için sıfıra indiği anlamına gelir! Bunun mesafeye dayalı kümeleme algoritmalarının çok büyük sonuçları vardır. Tüm mesafeler aynı gibi görünmeye başlar ve diğerinden daha fazla veya daha az olan herhangi bir mesafe, herhangi bir farklılık ölçüsünden ziyade verilerdeki daha rastgele dalgalanmadır!
Şekil 3, rastgele oluşturulmuş 2 boyutlu verileri ve karşılık gelen tüm mesafeleri göstermektedir. Standart Sapmanın Ortalamaya bölünmesiyle hesaplanan mesafedeki Varyasyon Katsayısı %45,9'dur. Benzer şekilde üretilen 5-D verilerinin karşılık gelen sayısı %26,5 ve 10-D için %19,1'dir. Kuşkusuz bu bir örnek, ancak eğilim, yüksek boyutlarda her mesafenin yaklaşık olarak aynı olduğu ve hiçbirinin yakın veya uzak olmadığı sonucunu desteklemektedir!
Şekil 3: Uzaklık Kümelemesi
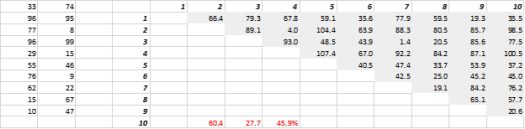
Yüksek boyut başka şeyleri de etkiler
Mesafeler ve hacimlerden ayrı olarak, boyutların sayısı başka pratik problemler yaratır. Çözüm çalışma zamanı ve sistem belleği gereksinimleri, boyutların sayısındaki artışla birlikte genellikle doğrusal olmayan bir şekilde yükselir. Uygulanabilir çözümlerdeki üstel artış nedeniyle birçok optimizasyon yöntemi global optimuma ulaşamaz ve yerel optimumla yetinmek zorunda kalır. Ayrıca, optimizasyon, kapalı form çözümü yerine gradyan inişi, genetik algoritma ve benzetilmiş tavlama gibi arama tabanlı algoritmaları kullanmalıdır. Daha fazla boyut, korelasyon olasılığını ortaya çıkarır ve regresyon yaklaşımlarında parametre tahmini zorlaşabilir.
Yüksek Boyutla Başa Çıkmak
Bu, başlı başına ayrı bir blog yazısı olacaktır, ancak korelasyon analizi, kümeleme, bilgi değeri, varyans enflasyon faktörü, temel bileşen analizi, boyutların sayısını azaltmanın yollarından bazılarıdır.
* Bir veri noktasının oluşturduğu değişkenlerin, gözlemlerin veya özelliklerin sayısına veri boyutu denir. Örneğin, uzaydaki herhangi bir nokta uzunluk, genişlik ve yükseklik olmak üzere 3 koordinat kullanılarak temsil edilebilir ve 3 boyutu vardır.
