Histogramları Kullanarak Yoğunluk Tahmini

Olasılık Yoğunluk Fonksiyonları (PDF'ler), uzayın bazı bölgelerinde bazı sürekli rastgele değişkenleri gözlemleme olasılığını tanımlar. Tek boyutlu rastgele değişken X için, PDF f(x)'in şu özellikleri izlediğini hatırlayın:

Değişkenin arasında değerler alma olasılığı

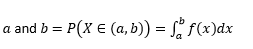
Değişkenin tam olarak eşit değerler alma olasılığı

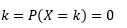
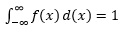
Bu tür PDF'leri gözlem örneklerinden tahmin etmek, Makine Öğreniminde yaygın bir sorundur. Bu, örnek gözlemlere dayalı olarak “doğru” dağılımı tahmin etmeye çalıştığımız ve ardından mevcut veya yeni gözlemlerin bazılarını aykırı değer veya değil olarak sınıflandırdığımız birçok aykırı değer algılama algoritmasında kullanışlıdır. Örneğin, sahtekarlığı yakalamakla ilgilenen bir otomobil sigortacısı, örneğin tampon değişimi gibi her bir üstyapı türü için talep tutarı talebini inceleyebilir ve çok yüksek olan herhangi bir tutarı potansiyel dolandırıcılık için işaretleyebilir. Başka bir örnekle, bir çocuk psikoloğu belirli bir görevi tamamlamak için geçen süreyi farklı çocuklar arasında inceleyebilir ve potansiyel araştırma için çok uzun veya çok kısa zaman alan çocukları işaretleyebilir.

Bu blog yazısında, her bir gözlem için olasılığı hesaplayabilmemiz ve bunun yaygın mı yoksa nadir mi olduğuna karar verebilmemiz için gözlem örneklerinden PDF'yi nasıl öğrenebileceğimizi tartışıyoruz.

Histogram kullanarak Yoğunluk Tahmini

İlk önce gösteri için bazı rastgele veriler üretiyoruz.

set.seed(123)
data <- c(rnorm(200, 10, 20), rnorm(200, 60, 30), runif(200, 120, 180)) # 600 points

Ardından, Şekil 1'deki gibi histogramı kullanarak anlamamız için onları görselleştiririz.

# Plot 1
hist(data, breaks=50, freq=F, main="Univariate Distribution", xlab="Data Value")
# Plot 2
hist(data, breaks=20, freq=F, main="", xlab="20 Data Bins", col='red', border='red')
par(new=T)
hist(data, breaks=100, freq=F, main="Univariate Distribution", xlab=NULL, xaxt='n', yaxt='n')

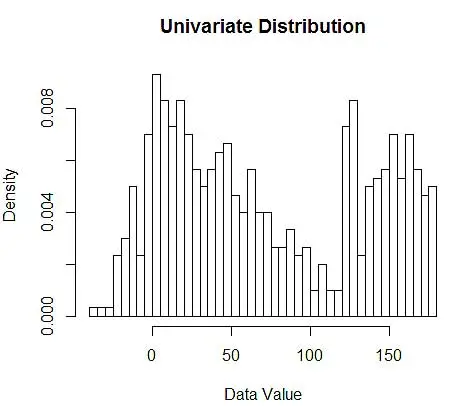
Histogramlar veri görselleştirme için çizelgeler olsa da, bunların ilk yoğunluk tahminimiz olduğunu da görebilirsiniz. Daha spesifik olarak, verileri kutulara bölerek ve yoğunluğun bu kutu aralığında sabit olduğunu ve toplam gözlem sayısının oranı olarak o kutuya düşen gözlem sayısına eşit değere sahip olduğunu varsayarak yoğunluğu tahmin edebiliriz.

Bu nedenle, tahmini PDF

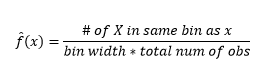
Ve yoğunluk tahminini etkileyecek olan bin-with hakkında varsayımda bulunduğunuzu anlıyorsunuz. Dolayısıyla bölme genişliği, histogram kullanan yoğunluk tahmin modelinin bir parametresidir . Ancak gözden kaçan gerçek şu ki, bir parametreyle daha çalışıyoruz – bu, first bin öğesinin başlangıç ​​konumudur . Bunun tüm kutular için yoğunluk tahminlerini nasıl etkileyebileceğini görebilirsiniz. Kutu genişliğinin etkisini görmek için Şekil 2, 20-binlik ve 100-binlik histogramlarla yoğunluk tahminlerini kaplar. Daha az/daha kalın bölmelerin düz yoğunluk tahmini verdiği, çok sayıda/daha ince bölmelerin ise değişen yoğunluk tahmini verdiği daire içine alınmış bölgeye bakın. Sarı nokta için yoğunluk tahminleri, iki farklı modelden 0,004 ila 0,008 arasında değişecektir.

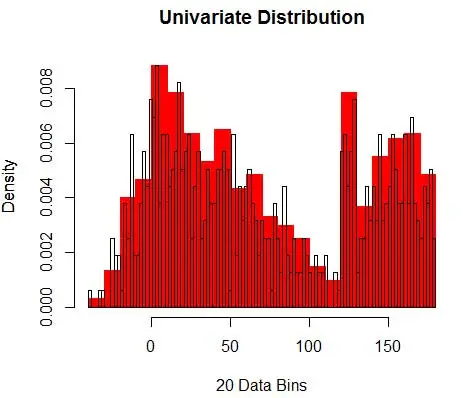
Bu nedenle, yoğunluk tahminini doğru yapmak için parametreleri doğru seçmek çok önemlidir. Buna geleceğiz, ancak histogramlarla ilgili başka sorunlar da olduğunu unutmayın. Histogramları kullanan yoğunluk tahminleri oldukça sarsıntılı ve süreksizdir . Yoğunluk, bir kutu için düzdür ve ardından, kutunun sonsuz küçüklükte dışındaki bir nokta için aniden büyük ölçüde değişir. Bu, yanlış tahminin sonucunu pratik problemler için daha da kötüleştirir.

Son olarak, örnekleme kolaylığı için tek boyutlu değişkenle çalışıyoruz, ancak pratikte çoğu problem çok boyutludur. Kutu sayısı boyutların sayısıyla üstel olarak arttığından, yoğunluğu tahmin etmek için gereken gözlem sayısı da artar . Aslında, milyonlarca gözlem olmasına rağmen, birçok kutunun boş kalması veya tek basamaklı gözlemler içermesi akla yatkındır. Her biri sadece 3 boyutta sadece 50 kutu ile doldurulması gereken 503 = 125000 hücremiz var. Bu, tekdüze dağılım varsayıldığında, bir milyon gözlem eğitim verisi varsayarak, hücre başına ortalama 8 gözlem anlamına gelir.

Doğru parametreler nasıl seçilir?

Kutu genişliği için n gözlem sayısı N bin için J gözlem oranı

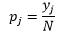
ve yoğunluk tahmini

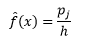
İstatistiksel teori, f(x)'in kutudaki yoğunluğun beklenen değeri olmasına rağmen, yoğunluk varyansının

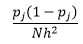
Bölme genişliğini n azaltarak daha iyi yoğunluk tahmini elde edebilsek de, çok ince bölme genişliği hakkında sezgisel olarak hissedebildiğimiz için tahminin varyansını artırırız. Optimum parametre setini tahmin etmek için bir defada çapraz doğrulama bırakma tekniğini kullanabiliriz. Biri hariç tüm gözlemleri kullanarak yoğunluğu tahmin edebilir ve ardından dışarıda kalan gözlemin yoğunluğunu hesaplayabilir ve tahmindeki hatayı ölçebiliriz. Bunu histogramlar için matematiksel olarak çözmek, verilen bölme genişliği için kayıp fonksiyonu için kapalı bir form çözümü verir.

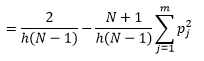
burada m kutu sayısıdır. Yukarıdakilerin teknik detayları bu derste [pdf] bulunmaktadır. Bu kayıp fonksiyonunu çeşitli kutu sayıları için çizebiliriz (Şekil 3)

getLoss <- function(n.break) {
N <- 600
res <- hist(data, breaks=n.break, freq=F)
bin <- as.numeric(res$breaks)
h <- bin[2]-bin[1]
p <- res$density
p <- p * h
return ( 2/(h*(N-1)) - ( (N+1)/(h*(N-1))*sum(p*p) ) )
}
loss.func <- data.frame(n=1:600)
loss.func$J <- sapply(loss.func$n, function(x) getLoss(x))
# Plot 3
plot(loss.func$n, loss.func$J, col='red', type='l')
opt.break <- max(loss.func[loss.func$J == min(loss.func$J), 'n'])
print(opt.break)
# Plot 4
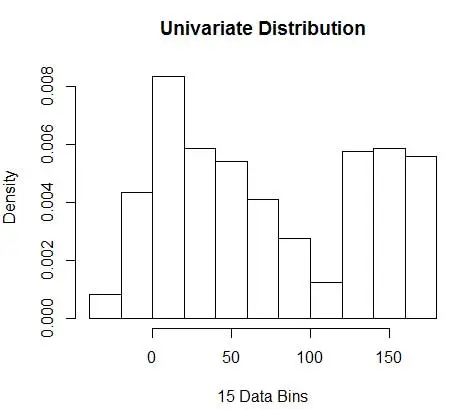
hist(data, breaks=opt.break, freq=F, main="Univariate Distribution", xlab="15 Data Bins")

ve en uygun sayıyı 15 olarak alın. Aslında 8-15 arası herhangi bir şey iyidir.

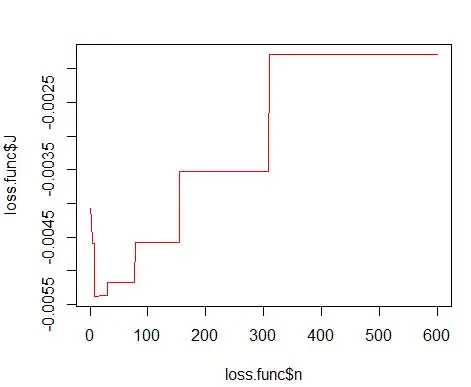
Sonuç olarak, Şekil 4'ün altında, yoğunluk değerlerinin yanı sıra ayrıntı düzeyi (optimum sapma-varyans değiş tokuşu ile) dengeleyen yoğunluk tahmini yer almaktadır.

Bu noktada biraz huzursuz hissediyorsanız, o zaman ben yanınızdayım. Kutu sayısı matematiksel olarak optimal olsa da, çok kaba bir tahmin gibi geliyor. En iyi işi neden yaptığımıza dair sezgisel bir his yok. Ve başlangıç ​​pozisyonu, süreksiz tahmin ve boyutsallık laneti ile ilgili diğer endişeleri de unutmamak gerekir. Üzülmeyin, daha iyi bir yol var. Bir sonraki yazımızda Çekirdekleri kullanarak Yoğunluk Tahmini hakkında konuşacağız.