Hiperuzayda Mesafeyi Ölçme

Analitik tekniklere yüzeysel olarak aşina olan herkes, uygulamaları için veri noktaları arasındaki mesafelere dayanan çok sayıda algoritma fark edebilirdi. Her gözlem veya veri örneği, genellikle çok boyutlu vektör olarak temsil edilir ve algoritmaya girdi, bu tür gözlemlerin her bir çifti arasında mesafeler gerektirir.

Mesafe hesaplama yöntemi, verilerin türüne bağlıdır - sayısal, kategorik veya karışık. Algoritmalardan bazıları yalnızca bir gözlem sınıfına uygulanırken, diğerleri birden çok gözlem üzerinde çalışır. Bu yazıda sayısal veriler üzerinde çalışan uzaklık ölçülerini ele alacağız. Belki de çok boyutlu hiperuzayda mesafeyi ölçmenin tek bir blog gönderisinde ele alınabileceklerden daha fazla yolu vardır ve her zaman daha yeni yollar icat edilebilir, ancak bazı ortak mesafe ölçümlerini ve bunların göreceli değerlerini inceliyoruz.

Blog gönderisinin geri kalanı için, şunu ima ediyoruz:

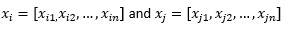
iki gözleme veya veri vektörüne atıfta bulunmak için.

Önce verileri hazırlayın…

Farklı mesafe ölçümlerini incelemeden önce verileri hazırlamamız gerekiyor:

Sayısal vektöre dönüşüm

Hem sayısal hem de kategorik boyutları içeren karma gözlem için ilk adım, kategorik boyutu fiilen sayısal boyut(lar)a dönüştürmektir. Üç potansiyel değere sahip kategorik bir boyut, ikili değerlerle iki veya üç sayısal boyuta dönüştürülebilir. Bu kategorik değişken zorunlu olarak üç değerden birini aldığından, üç sayısal boyuttan biri diğer ikisi ile mükemmel bir şekilde ilişkilendirilecektir. Bu, uygulamanıza bağlı olarak uygun olabilir veya olmayabilir.

Eğer gözlem, metin dizisi (değişen uzunluktaki cümleler) veya genom dizisi (sabit uzunluklu diziler) gibi tamamen kategorik ise, o zaman bazı özel mesafe ölçüleri, verileri sayısal biçime dönüştürmeden doğrudan uygulanabilir. Bu algoritmaları bir sonraki yazıda tartışacağız.

normalleştirme

Kullanım durumunuza bağlı olarak, herhangi bir boyuttaki mesafenin gözlemler arasındaki toplam mesafeyi gereksiz yere etkilememesi için her bir boyutu aynı ölçekte normalleştirmek isteyebilirsiniz. Aynı şey k-Means algoritmasında da tartışıldı. İki tür normalleştirme mümkündür:

Aralık normalleştirme (yeniden ölçeklendirme) , her boyuttan minimum değeri çıkararak ve ardından o boyuttaki değer aralığına bölerek verileri 0-1 aralığında olacak şekilde normalleştirir.

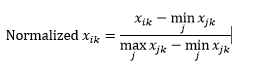
Aralık normalizasyonu ile ilgili ilk sorun, görünmeyen bir değerin 0-1 aralığının ötesinde normalize edilebilmesidir. Bununla birlikte, bu genellikle çoğu mesafe metriği için bir endişe değildir, ancak algoritma negatif değerleri işleyemiyorsa, bu sorun olabilir. İkinci sorun, bunun büyük ölçüde aykırı değerlere bağlı olmasıdır. Bir gözlemin bir boyut için çok aşırı (yüksek veya düşük) değeri varsa, diğer gözlemler için o boyut için normalleştirilmiş değer bir araya toplanacak ve ayırt edici güçlerini kaybedecektir.

Standart normalleştirme (z-ölçeklendirme) , her gözlemin o boyutundan ortalamayı çıkararak ve ardından tüm gözlemlerde o boyutun değerinin standart sapmasına bölerek, boyutu 0 ortalama ve 1 standart sapmaya sahip olacak şekilde normalleştirir.

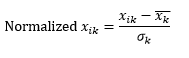
Bu genellikle verileri kabaca -5 ila +5 aralığında tutar ve aşırı değerin etkisini önler.

İki gözlemin z-ölçeklendirmesini simüle ettik. Simüle edildi, çünkü her boyutun ortalamasını ve standart sapmasını hesaplamak için gerçekten ikiden fazla gözleme ihtiyacımız var ve burada her boyut için bu sayıların her ikisini de varsaydık.

Sonra mesafeyi hesaplayın…

Öklid mesafesi - aka "kuş uçuşu mesafesi" - iki nokta arasındaki çok boyutlu hiperuzayda en kısa mesafedir. Bunu 2B düzlemde veya 3B uzayda (bu bir çizgidir) bilirsiniz, ancak benzer konsept daha yüksek boyutlara uzanır. n-boyutlu uzayda vektörler arasındaki Öklid uzaklığı şu şekilde hesaplanır:

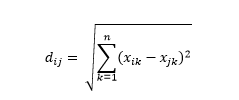
Dönüştürülen veri vektörü örnekleri için bu,

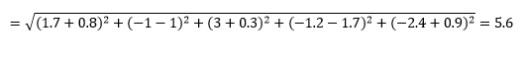
Bu en yaygın ölçümdür ve çoğu uygulama için genellikle çok uygundur. Bunun bir varyantı, sadece kare farklarının toplamı olan kare-Öklid mesafesidir.

Manhattan mesafesi - New York'taki Manhattan sokaklarının Doğu-Batı-Kuzey-Güney ızgara benzeri yapısından dolayı adlandırılan - eksenlere paralel hareket ederken iki nokta arasındaki mesafedir.

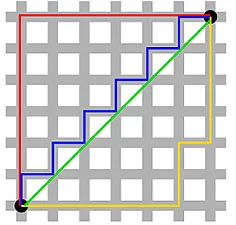
Manhattan Mesafesi
Öklid Uzaklığı

Bu şu şekilde hesaplanır

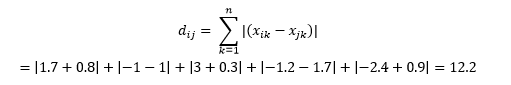
Bu, mesafenin makine öğrenimi “farklılık” anlamından ziyade gerçek, fiziksel anlamda kullanıldığı bazı uygulamalarda faydalı olabilir. Örneğin, bir noktaya ulaşmak için itfaiye aracının kat ettiği mesafeyi hesaplamanız gerekiyorsa, bunu kullanmak daha pratiktir.

Canberra mesafesi , Manhattan mesafesinin ağırlıklı varyantıdır ve şu şekilde hesaplanır:

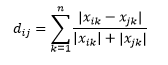
L-norm mesafesi , ikinin üzerindeki uzantıdır - veya yukarıdaki ikinin, L-norm mesafesinin belirli durumları olduğunu söyleyebilirsiniz - ve şu şekilde tanımlanır:

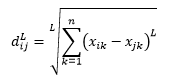
burada L pozitif bir tam sayıdır. Bunu kullanmam gereken herhangi bir durumla karşılaşmadım, ancak bunu bilmek yine de iyi bir olasılık. Örneğin 3-norm mesafe olacak

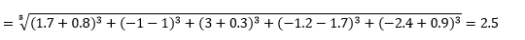
Pozitif veya negatif mesafe katkılarının iptal edilmesini istemediğimizden, L'nin genellikle tamsayı olması gerektiğini unutmayın.

Minkowski mesafesi , L'nin 0'dan kesirli değerler dahil olmak üzere herhangi bir değeri alabileceği L-norm mesafesinin genelleştirilmesidir. p mertebesinden Minkowski uzaklığı şu şekilde tanımlanır:

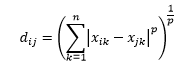
Kosinüs mesafesi , her biri iki gözlemi temsil eden ve veri noktasının orijine birleştirilmesiyle oluşturulan iki vektör arasındaki açının ölçüsüdür. Kosinüs mesafesi 0 (tamamen aynı) ile 1 (bağlantı yok) arasında değişir ve şu şekilde hesaplanır:

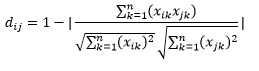
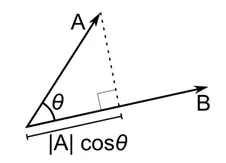
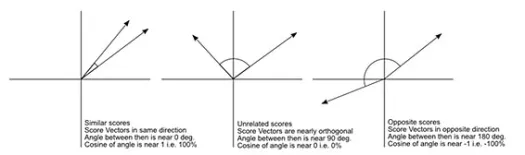
Bu, kategorik verilerle çalışırken daha yaygın bir mesafe ölçüsü olmakla birlikte, sayısal vektör için de tanımlanabilir. Sayısal vektörlerimiz için bu,

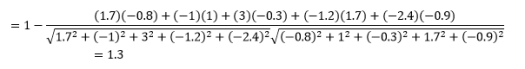
Ancak uyarıları dikkate alın…

Bunun geleceğini biliyordun, değil mi? Analitik sadece bir grup matematiksel formül olsaydı, bunu yapmak için sizin gibi akıllı insanlara ihtiyacımız olmayacaktı.

Unutulmaması gereken ilk şey, farklı metriklerle hesaplanan mesafelerin farklı olmasıdır. 1,3'lük Kosinüs mesafesinin en küçük olduğunu ve bu nedenle vektörlerin en yakın olduğunu gösterdiğini düşünmek isteyebilirsiniz, ancak bu doğru bir yorumlama şekli değildir. Farklı yöntemler arasındaki mesafeler karşılaştırılamaz ve yalnızca aynı yöntem altındaki farklı gözlem çiftleri arasındaki mesafeler karşılaştırılabilir. Mesafelerin göreceli anlamı vardır ve kendi başlarına mutlak bir anlamı yoktur .

Bu, doğru mesafe metriğinin nasıl seçileceğine ilişkin bir sonraki soruya götürür. Ne yazık ki, gerçek bir cevap yok. Veri türüne, bağlama, iş sorununa, uygulamaya ve model eğitim yöntemine bağlı olarak farklı metrikler farklı sonuçlar verir. Doğru metriğe karar vermek için muhakeme kullanmanız, varsayımlarda bulunmanız veya model performansını test etmeniz gerekecektir .

İkinci uyarı, boyutsallık laneti hakkında sık sık tekrarladığım bir uyarıdır. Daha yüksek boyutlarda, mesafeler sezgisel olarak düşündüğümüz şekilde davranmaz ve analist herhangi bir metriği kullanırken son derece dikkatli olmalıdır.

Üçüncü uyarı, üç gözlem arasındaki mesafeler arasındaki ilişki ile ilgilidir. Bazı metrikler üçgen eşitsizliğini desteklerken diğerleri desteklemez . Üçgen eşitsizliği, herhangi bir k ara noktasından ziyade, i noktasından j noktasına doğrudan gitmenin her zaman en kısa yol olduğu anlamına gelir. Matematiksel olarak,

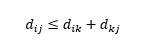
Uygulamanıza bağlı olarak, bu, mesafe metriğinin gerekli özelliği olabilir veya olmayabilir.

Oh, bir şey daha, "mesafe", "benzerlik"in zıttıdır. Mesafeyi artırın, benzerliği azaltın ve bunun tersi de geçerlidir. Kümeleme algoritmaları mesafeler üzerinde çalışır ve öneri algoritmaları benzerlik üzerinde çalışır, ancak aslında aynı şeyden bahsediyorlar.

Peki, uzaklık sayısını benzerlik sayısına nasıl dönüştürebilirsiniz?