维度诅咒
已发表: 2015-07-08什么是维度诅咒
维度诅咒是指在高维空间*中工作时观察到的数据的非直观属性,特别是与距离和体积的可用性和解释有关。 这是我在机器学习和统计中最喜欢的主题之一,因为它具有广泛的应用(不特定于任何机器学习方法),它非常违反直觉,因此令人敬畏,它对任何分析技术都有深远的应用,并且它有一个“酷”可怕的名字,就像一些埃及诅咒!
为了快速掌握,请考虑以下示例:假设您在 100 米线上丢了一枚硬币。 你是怎么找到它的? 很简单,只要走线上搜索。 但是如果它是 100 x 100 平方米呢? 场地? 它已经变得艰难,试图在(大致)足球场上寻找一枚硬币。 但是如果它是 100 x 100 x 100 立方米的空间呢? 要知道,现在的足球场有三十层楼高。 祝你在那里找到一枚硬币! 这本质上是“维度的诅咒”。
许多 ML 方法使用距离测量
大多数分割和聚类方法依赖于计算观测值之间的距离。 众所周知的 k-Means 分割将点分配给最近的中心。 DBSCAN 和层次聚类也需要距离度量。 基于分布和密度的异常值检测算法还利用相对于其他距离的距离来标记异常值。
像k-Nearest Neighbors方法这样的监督分类解决方案也使用观测值之间的距离来将类别分配给未知观测值。 支持向量机方法涉及根据观察与内核之间的距离围绕选定内核转换观察。
推荐系统的常见形式涉及用户和项目属性向量之间基于距离的相似性。 即使使用其他形式的距离,维度的数量也会在分析设计中发挥作用。
最常见的距离度量之一是欧几里得距离度量,它只是多维超空间中两点之间的线性距离。 n 维空间中点 i 和点 j 的欧几里得距离可以计算为:
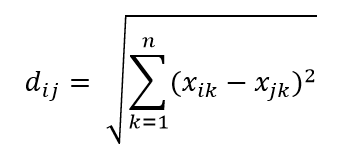
距离在高维度中造成严重破坏
考虑简单的数据采样过程。 假设图 1 中的黑色外框是数据域,数据点在整个体积中均匀分布,并且我们希望对 1% 的观测值进行采样,并用红色内框包围。 黑盒子是多维空间中的超立方体,每边代表该维度中的值范围。 对于图 1 中的简单 3 维示例,我们可能有以下范围:
图 1:采样
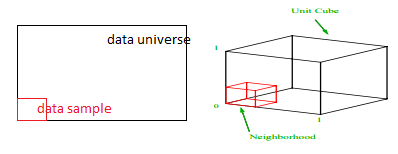
我们应该采样每个范围的比例以获得 1% 的样本? 对于二维,10% 的范围将实现整体 1% 的采样,因此我们可以选择 x∈(0,10) 和 y∈(0,50) 并期望捕获所有观测值的 1%。 这是因为 10%2=1%。 对于 3 维,您认为这个比例会更高还是更低?
尽管我们现在的搜索是在另外的方向上,但比例实际上增加到了 21.5%。 不仅增加了,而且仅仅增加了一个维度,它增加了一倍! 你可以看到,我们必须覆盖几乎每个维度的五分之一才能获得整体的百分之一! 在 10 维中,这个比例为 63%,而在 100 维中——这在任何现实机器学习中并不少见——必须沿每个维度采样 95% 的范围才能采样 1% 的观察值! 之所以会出现这种令人费解的结果,是因为在高维度中,即使数据点均匀分布,它们的分布也会变得更大。

这对实验和抽样的设计有影响。 过程在计算上变得非常昂贵,即使在样本量仍然远小于总体的情况下,采样渐近接近总体。
考虑高维的另一个巨大后果。 许多算法测量两个数据点之间的距离,以参考一些预定义的距离阈值来定义某种接近度(DBSCAN、内核、k-Nearest Neighbour)。 在二维中,我们可以想象如果一个点落在另一个点的一定半径内,那么两个点就在附近。 考虑图 2 中的左图。黑色正方形内的均匀间隔点落在红色圆圈内的比例是多少? 那是关于
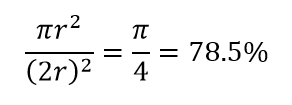
图 2:接近度
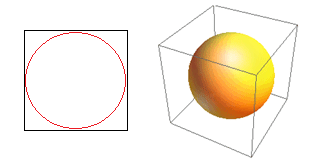
因此,如果您在正方形内放置可能的最大圆圈,则您覆盖了正方形的 78%。 然而,立方体内可能的最大球体仅覆盖
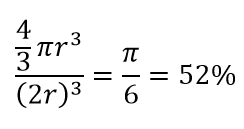
的音量。 仅 10 维,这个体积就成倍减少到 0.24%! 它本质上意味着在高维世界中,每个数据点都在角落,没有什么是真正的体积中心,或者换句话说,中心体积减少到没有,因为(几乎)没有中心! 这对基于距离的聚类算法产生了巨大的影响。 所有距离开始看起来都一样,任何或多或少的距离都是数据的随机波动,而不是任何不同的度量!
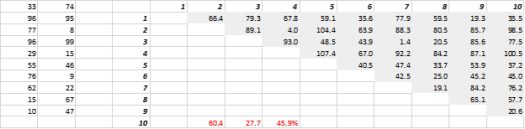
图 3 显示了随机生成的二维数据和相应的全对全距离。 距离变化系数(计算为标准偏差除以平均值)为 45.9%。 类似生成的 5-D 数据的相应数量为 26.5%,而 10-D 为 19.1%。 诚然,这是一个样本,但趋势支持这样的结论,即在高维中,每个距离都大致相同,没有近或远!
图 3:距离聚类
高维也会影响其他东西
除了距离和体积之外,维度的数量还会产生其他实际问题。 解决方案运行时和系统内存需求通常会随着维度数量的增加而非线性升级。 由于可行解的指数增加,许多优化方法无法达到全局最优,不得不与局部最优凑合。 此外,优化必须使用梯度下降、遗传算法和模拟退火等基于搜索的算法,而不是封闭形式的解决方案。 更多维度引入了相关性的可能性,并且在回归方法中参数估计可能变得困难。
处理高维
这将是单独的博客文章,但相关性分析、聚类、信息值、方差膨胀因子、主成分分析是可以减少维度数量的一些方法。
*组成数据点的变量、观察值或特征的数量称为数据维度。 例如,空间中的任何点都可以用长、宽、高的 3 个坐标来表示,并且具有 3 个维度
