在超空间测量距离

任何粗略熟悉分析技术的人都会注意到许多算法依赖于数据点之间的距离来进行应用。 每个观察或数据实例通常表示为多维向量，算法的输入需要每对这样的观察之间的距离。

距离计算方法取决于数据类型——数值、分类或混合。 一些算法只适用于一类观察，而另一些则适用于多种。 在这篇文章中，我们将讨论适用于数值数据的距离度量。 在多维超空间中测量距离的方法可能比单个博客文章中所能涵盖的方法更多，而且人们总是可以发明新的方法，但我们会研究一些常见的距离度量及其相对优点。

出于博客文章其余部分的目的，我们暗示

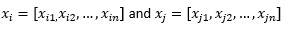
指两个观察或数据向量。

首先准备好数据……

在我们查看不同的距离指标之前，我们需要准备数据：

转换为数值向量

对于同时包含数值维度和分类维度的混合观察，第一步是将分类维度实际转换为数值维度。 具有三个潜在值的分类维度可以转换为具有二进制值的两个或三个数字维度。 由于该分类变量必须采用三个值之一，因此三个数值维度之一将与其他两个完全相关。 根据您的应用程序，这可能会也可能不会。

如果观察是纯分类的，例如文本字符串（可变长度的句子）或基因组序列（固定长度的序列），那么可以直接应用一些特殊的距离度量，而无需将数据转换为数字格式。 我们将在下一篇文章中讨论这些算法。

正常化

根据您的用例，您可能希望以相同的比例对每个维度进行归一化，以便沿任何一个维度的距离不会过度影响观测值之间的总体距离。 在 k-Means algorithm 中讨论了同样的事情。 有两种可能的归一化：

范围归一化（重新缩放）通过从每个维度减去最小值然后除以该维度中的值范围来将数据归一化为 0-1 范围。

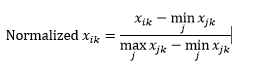
范围归一化的第一个问题是看不见的值可能被归一化到 0-1 范围之外。 虽然，对于大多数距离度量来说，这通常不是问题，但如果算法不能处理负值，那么这可能是个问题。 第二个问题是这高度依赖于异常值。 如果一个观测值对于某个维度具有非常极端的（高或低）值，则其他观测值的该维度的归一化值将挤在一起并失去它们的判别能力。

标准归一化（z 标度）通过从每个观测值的维度中减去均值，然后除以所有观测值中该维度值的标准差，将维度归一化为 0 均值和 1 标准差。

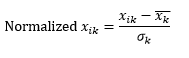
这通常使数据大致保持在-5到+5范围内，并避免极值的影响。

我们模拟了两个观测值的 z 缩放。 模拟，因为我们确实需要两个以上的观测值来计算每个维度的均值和标准差，并且我们在这里为每个维度假设了这两个数字。

然后计算距离...

欧几里得距离——又名“乌鸦飞”的距离——是多维超空间中两点之间的最短距离。 您在 2D 平面或 3D 空间（这是一条线）中熟悉这一点，但类似的概念扩展到更高的维度。 n维空间中向量之间的欧几里得距离计算为

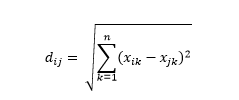
对于转换后的数据向量示例，这是

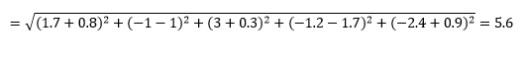
这是最常见的指标，通常非常适合大多数应用程序。 它的一个变体是平方欧几里得距离，它只是平方差的总和。

曼哈顿距离- 因纽约曼哈顿街道的东西 - 南北 - 南网格结构而得名 - 是平行于轴穿过时两点之间的距离。

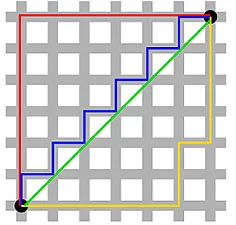
曼哈顿距离
欧几里得距离

这计算为

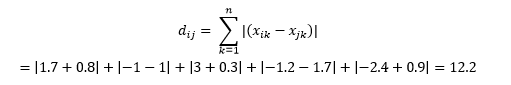
这在某些应用程序中可能很有用，其中距离用于真实的物理意义，而不是机器学习的“差异”意义。 例如，如果您需要计算消防车到达某个点的距离，那么使用它更实用。

堪培拉距离是曼哈顿距离的加权变体，计算为

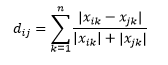
L-范数距离是以上两个的延伸——或者你可以说以上两个是 L-范数距离的特定情况——并且被定义为

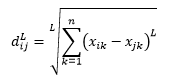
其中 L 是一个正整数。 我没有遇到任何需要使用它的情况，但这仍然很高兴知道可能性。 例如 3 范数距离将是

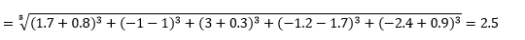
请注意，L 通常应该是偶数，因为我们不希望正或负距离贡献抵消。

Minkowski 距离是 L 范数距离的推广，其中 L 可以取从 0 到包括小数值的任何值。 p阶的闵可夫斯基距离定义为

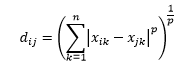
余弦距离是两个向量之间角度的度量，每个向量代表两个观察值，并通过将数据点连接到原点而形成。 余弦距离范围从 0（完全相同）到 1（无连接），计算如下

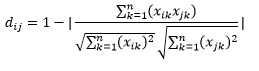
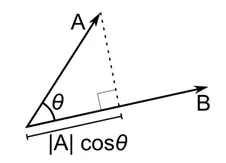
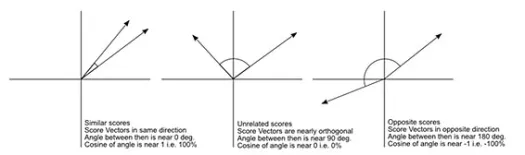
虽然在处理分类数据时这是更常见的距离度量，但也可以为数值向量定义。 对于我们的数值向量，这将是

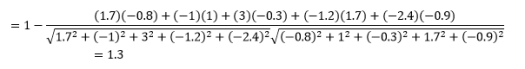
但请注意警告......

你知道这会来的，不是吗？ 如果分析只是一堆数学公式，我们不需要像你这样聪明的人来做。

首先要注意的是，不同度量计算的距离是不同的。 您可能会认为 1.3 的余弦距离是最小的，因此表明向量是最接近的，但这不是正确的解释方式。 无法比较不同方法之间的距离，只能比较同一方法下不同观测值对之间的距离。 距离本身有相对意义，没有绝对意义。

这就引出了下一个问题，即如何选择正确的距离度量。 不幸的是，没有真正的答案。 根据数据类型、上下文、业务问题、应用程序和模型训练方法，不同的指标给出不同的结果。 您将不得不使用判断、做出假设或测试模型性能来决定正确的指标。

第二个警告是我经常重复的一个关于维度诅咒的问题。 在更高的维度中，距离的行为方式并不像我们直观地认为的那样，分析师在使用任何指标时都必须非常谨慎。

第三个警告是关于三个观察之间的距离之间的关系。 一些指标支持三角不等式，而另一些则不支持。 三角不等式意味着从点 i 直接到点 j 总是最短的，而不是通过任何中间点 k。 数学上，

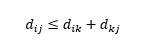
根据您的应用程序，这可能是距离度量的必需属性，也可能不是。

哦，还有一件事， “距离”与“相似”相反。 距离越高，相似度越低，反之亦然。 聚类算法适用于距离，推荐算法适用于相似性，但本质上它们是在谈论同一件事。

那么，如何将距离数转换为相似数呢？