使用 Excel 回归更好地理解 KPI

已发表: 2021-10-23

我们在 Hanapin 的一群人最近参加了由着名的 Microsoft Excel 专家 Wayne Winston 博士指导的为期 21 天的免费 Excel 课程。课程本身起初感觉很慢，但最终揭示了一些我从未知道的 Excel 功能。对我而言，其中最令人兴奋的是无需高级统计软件（如 STATA）即可回归多个变量的能力。在这篇文章中，我将分享在 Excel 中设置和运行回归的分步步骤，以及该工具如何帮助您进行 PPC 分析和帐户管理。

对不起，我退步了

在我们深入研究技术实现之前，您可能会想，“到底什么是回归？” 简而言之，回归着眼于变量之间的关系。对于任何因变量（“Y”），哪组自变量（“Xs”）对变异 Y 有贡献，回归模型解释了多少这种行为？（有关回归分析的深入回顾，请参见此处）

线性回归（或多元线性回归）是最常见的，拟合成以下形式的求和方程：

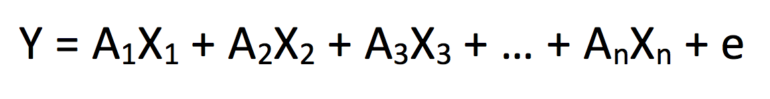
其中 Y 是因变量，X ₁ – X _n代表一组n 个自变量，A ₁ – A _n是对应于 X ₁ – X _n的系数常数。这是基本的统计模型构建，因此我们认识到每次“y”迭代的预测结果和观察结果之间会存在一些不一致。因此，误差项“+e”被添加以解释这种差异。

为什么在 PPC 中回归？

回归可用于任何数量的分析。例如，您可能需要考虑每次点击费用出价更改对平均点击费用的影响。排名、错失的印象份额或质量得分。您可以检查哪个元素（预期点击率、着陆页体验或广告相关性）对您的帐户、广告系列或关键字级别的质量得分影响最大。也许，正如我们将在下面的示例中看到的，您想了解搜索和展示广告的每次点击费用和转化率在您帐户的整体每次转化费用中所起的作用。

无论您的最终目标是什么，设置和确定回归模型值的过程都是相同的。

第 1 步：准备数据

与任何分析一样，一个好的结果需要正确准备的高质量数据。为了获得良好的回归结果，您需要足够数量的数据（至少与自变量的数量一样多的数据点，但您可用的数据越多，您的回归模型就越准确）。要增加数据点的数量，您可以考虑按天、周或月（取决于所检查的时间范围）对数据进行分段。

在我们的示例中，我们在 Adwords 中使用了过去 24 个月的数据。下载活动报告（按月细分）后，我们创建一个数据透视表以按月和活动类型检查点击次数、成本和转化次数：

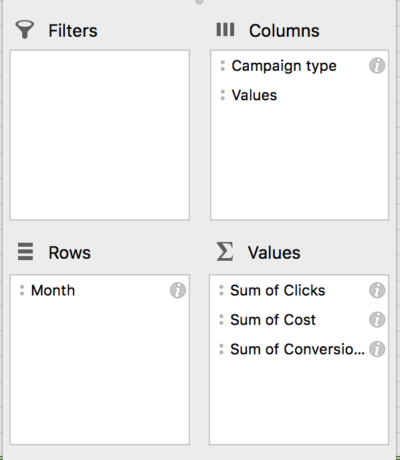
从这里，我们可以计算每个网络的 CPA、CPC 和 CVR，以及总 CPA。然后只需将数据快速复制并粘贴到新工作表中，我们就可以开始回归了！

第 2 步：构建模型（选择变量）

模型构建有两个主要组成部分：周到的规划和灵活的修订。深思熟虑的计划是考虑哪些变量在逻辑上最适合您的模型（以及哪些数据可供使用）。在计划阶段多花一点时间可以节省您以后测试和重新测试模型的时间和理智。即使进行了仔细的准备，您可能仍然需要在回归和识别重要和不重要的变量时灵活地修改模型。

选择自变量时的两个重要注意事项：

自变量应该与因变量具有可想象的逻辑关系（即东京的平均降雨量和威斯康星州的心脏病发作次数在我要检查的相关性列表中很低）
自变量不应相互高度相关（即，将成本、点击次数和 CPC 作为自变量包含在同一回归中会导致模型中的多重共线性错误）

在我们的示例中，我们想看看是什么推动了我们的帐户 CPA。我们知道在 Adwords 中有两个投放广告的网络——搜索网络和展示广告网络——并且我们知道推动每个网络的 CPA（成本/转化）的两个主要变量是 CPC（成本/点击）和 CVR（转化/点击））。

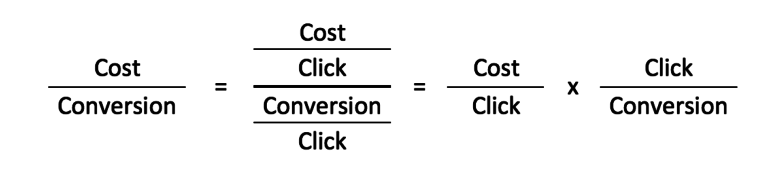
因此，我们将首先分别对搜索和展示的 CPC 和 CVR 上的 CPA 进行回归，以确定哪些自变量是重要的，因此应包含在我们的最终模型中。

第 3 步：回归和修正

在 Excel 中运行回归：

1. 在 Excel 中启动回归之前，首先检查以确保自变量（数据列）彼此相邻。

2. 接下来，确认为 Excel 启用了“分析工具库”加载项（启用后在“数据”功能区中可见）。

3. 在数据分析工具箱中，选择“回归”。

4. 输入您的因变量 (Y) 范围和自变量 (X) 范围，如果您选择包括列标题，请选择“标签”

5. 为回归输出选择一个位置（新的或现有的工作表）

6. 如果要检查和删除数据中的异常值，请选择“残差”

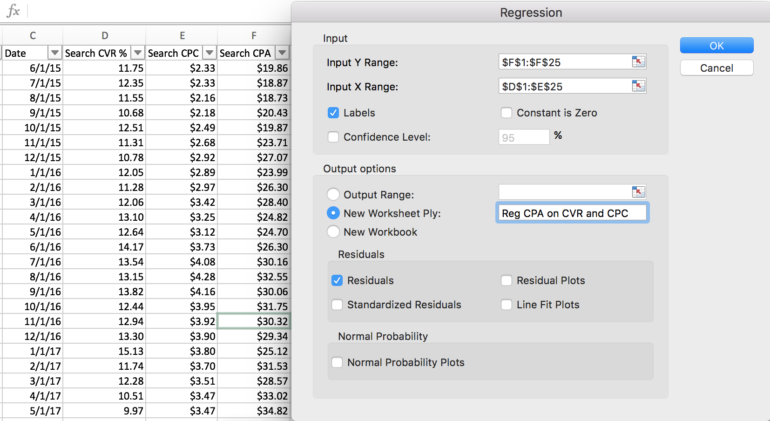
7. 单击“确定”运行回归。您将自动导航到包含输出摘要和详细信息的工作表。

8. 如果对回归输出的检查显示自变量不显着（通常，p 值大于 .1）或低于预期的 R 平方（参见下面的“A”），您可以根据需要重复该过程以细化模型。

第 4 步：了解输出

第一次查看摘要输出可能会令人生畏和沮丧。为方便起见，下面突出显示了输出的关键部分，以帮助您评估刚刚构建的回归模型。

(A) R 方和调整后的 R 方：这是衡量模型“拟合”数据的程度。简而言之，R 方告诉您选择的自变量解释了因变量中的多少变化。调整后的 R 方基本相同，但也考虑了包含的自变量的数量，提供了稍微更准确的度量。（没有“好”或“正确”的 R 方，因为它取决于您使用的模型和数据的类型，但越高越好）。

(B) 标准误差：预测结果与实际结果之间的平方差之和的平方根。对于正态分布，大约 65% 的残差（参见下面的“E”）将小于 1 标准误差，95% 将小于 2。大于标准误差两倍的残差通常被标记为数据中的异常值。

(D) 自变量的 P 值：通俗地说，P 值说明自变量的显着性。低 P 值是显着的（目标是小于 0.1），而高 P 值表明感知的相关性可能是纯粹的机会。在“灵活修订”阶段应排除具有高 P 值的自变量。

(E) 残差：这显示了每次迭代的因变量的预测值与实际记录值之间的差异。如上所述，大多数残差应小于 1 标准误差，几乎所有残差都应小于 2 * 标准误差的值。您可以决定是在模型中包含还是排除任何已识别的异常值（残差大于标准误差的两倍）。

第 5 步：把它放在一起（外卖部分！）

在运行三个回归之后，我们发现以下三个方程式将搜索和展示广告的 CPC 和 CVR 与网络和总 CPA 相关联：

这些等式验证了我们已经知道的（或认为我们知道的）：搜索和展示广告的 CPC 和 CVR 都在我们的总 CPA 行为中发挥着重要作用。然而，除此之外，他们还揭示了标准热图不会的三件事。

搜索 CPC 的增加对搜索 CPA 的影响是搜索 CVR 的同等提升的 3.5 倍
展示广告每次点击费用波动对展示广告每次转化费用的影响几乎是展示广告视频转化费用的 5 倍
总体而言，展示广告网络性能的变化对总 CPA 的影响比搜索网络性能的类似变化幅度更大

由此可知，如果我的目标是降低总 CPA，那么展示广告网络每次点击费用是第一大优化目标。搜索 CPC 和展示广告 CVR 紧随其后，搜索 CVR 是我最不重要的。

回归是一个强大的工具，也是 PPC 经理工具带的一个很好的补充。这个基本示例仅展示了回归可以帮助您了解您钟爱的 KPI 之间关系的众多方式中的一种。我们希望您在 Excel 中测试或继续使用回归功能，并在 Twitter 上与我们分享您的经验/想法/发现！