維度詛咒
已發表: 2015-07-08什麼是維度詛咒
維度詛咒是指在高維空間*中工作時觀察到的數據的非直觀屬性,特別是與距離和體積的可用性和解釋有關。 這是機器學習和統計中我最喜歡的主題之一,因為它具有廣泛的應用(不特定於任何機器學習方法),它非常違反直覺,因此令人敬畏,它對任何分析技術都有深遠的應用,並且它有一個“酷”可怕的名字,就像一些埃及詛咒!
為了快速掌握,請考慮以下示例:假設您在 100 米線上丟了一枚硬幣。 你是怎麼找到它的? 很簡單,只要走線上搜索。 但是如果它是 100 x 100 平方米呢? 場地? 它已經變得艱難,試圖在(大致)足球場上尋找一枚硬幣。 但是如果它是 100 x 100 x 100 立方米的空間呢? 要知道,現在的足球場有三十層樓高。 祝你在那裡找到一枚硬幣! 這本質上是“維度的詛咒”。
許多 ML 方法使用距離測量
大多數分割和聚類方法依賴於計算觀測值之間的距離。 眾所周知的 k-Means 分割將點分配給最近的中心。 DBSCAN 和層次聚類也需要距離度量。 基於分佈和密度的異常值檢測算法還利用相對於其他距離的距離來標記異常值。
像k-Nearest Neighbors方法這樣的監督分類解決方案也使用觀測值之間的距離來將類別分配給未知觀測值。 支持向量機方法涉及根據觀察與內核之間的距離圍繞選定內核轉換觀察。
推薦系統的常見形式涉及用戶和項目屬性向量之間基於距離的相似性。 即使使用其他形式的距離,維度的數量也會在分析設計中發揮作用。
最常見的距離度量之一是歐幾里得距離度量,它只是多維超空間中兩點之間的線性距離。 n 維空間中點 i 和點 j 的歐幾里得距離可以計算為:
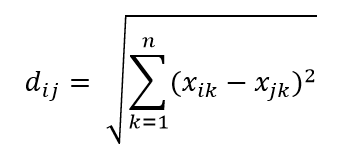
距離在高維度中造成嚴重破壞
考慮簡單的數據採樣過程。 假設圖 1 中的黑色外框是數據域,數據點在整個體積中均勻分佈,並且我們希望對 1% 的觀測值進行採樣,並用紅色內框包圍。 黑盒子是多維空間中的超立方體,每邊代表該維度中的值範圍。 對於圖 1 中的簡單 3 維示例,我們可能有以下範圍:
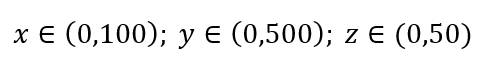
圖 1:採樣
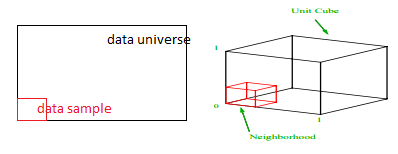
我們應該採樣每個範圍的比例以獲得 1% 的樣本? 對於二維,10% 的範圍將實現整體 1% 的採樣,因此我們可以選擇 x∈(0,10) 和 y∈(0,50) 並期望捕獲所有觀測值的 1%。 這是因為 10%2=1%。 對於 3 維,您認為這個比例會更高還是更低?
儘管我們現在的搜索是在另外的方向上,但比例實際上增加到了 21.5%。 不僅增加了,而且僅僅增加了一個維度,它增加了一倍! 你可以看到,我們必須覆蓋幾乎每個維度的五分之一才能獲得整體的百分之一! 在 10 維中,這個比例為 63%,而在 100 維中——這在任何現實機器學習中並不少見——必須沿每個維度採樣 95% 的範圍才能採樣 1% 的觀察值! 之所以會出現這種令人費解的結果,是因為在高維度中,即使數據點均勻分佈,它們的分佈也會變得更大。

這對實驗和抽樣的設計有影響。 過程在計算上變得非常昂貴,即使在樣本量仍然遠小於總體的情況下,採樣漸近接近總體。
考慮高維的另一個巨大後果。 許多算法測量兩個數據點之間的距離,以參考一些預定義的距離閾值來定義某種接近度(DBSCAN、內核、k-Nearest Neighbour)。 在二維中,我們可以想像如果一個點落在另一個點的一定半徑內,那麼兩個點就在附近。 考慮圖 2 中的左圖。黑色正方形內的均勻間隔點落在紅色圓圈內的比例是多少? 那是關於
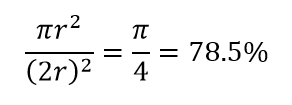
圖 2:接近度
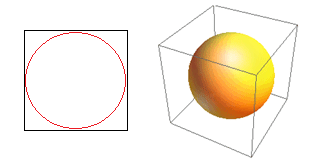
因此,如果您在正方形內放置可能的最大圓圈,則您覆蓋了正方形的 78%。 然而,立方體內可能的最大球體僅覆蓋
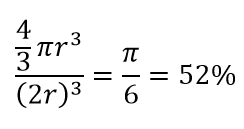
的音量。 僅 10 維,這個體積就成倍減少到 0.24%! 它本質上意味著在高維世界中,每個數據點都在角落,沒有什麼是真正的體積中心,或者換句話說,中心體積減少到沒有,因為(幾乎)沒有中心! 這對基於距離的聚類算法產生了巨大的影響。 所有距離開始看起來都一樣,任何或多或少的距離都是數據的隨機波動,而不是任何不同的度量!
圖 3 顯示了隨機生成的二維數據和相應的全對全距離。 距離變化係數(計算為標準偏差除以平均值)為 45.9%。 類似生成的 5-D 數據的相應數量為 26.5%,而 10-D 為 19.1%。 誠然,這是一個樣本,但趨勢支持這樣的結論,即在高維中,每個距離都大致相同,沒有近或遠!
圖 3:距離聚類
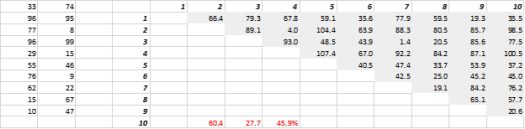
高維也會影響其他東西
除了距離和體積之外,維度的數量還會產生其他實際問題。 解決方案運行時和系統內存需求通常會隨著維度數量的增加而非線性升級。 由於可行解的指數增加,許多優化方法無法達到全局最優,不得不與局部最優湊合。 此外,優化必須使用梯度下降、遺傳算法和模擬退火等基於搜索的算法,而不是封閉形式的解決方案。 更多維度引入了相關性的可能性,並且在回歸方法中參數估計可能變得困難。
處理高維
這將是單獨的博客文章,但相關分析、聚類、信息價值、方差膨脹因子、主成分分析是可以減少維度數量的一些方法。
*組成數據點的變量、觀察值或特徵的數量稱為數據維度。 例如,空間中的任何點都可以用長、寬、高的 3 個坐標來表示,並且具有 3 個維度
