使用直方圖進行密度估計
已發表: 2015-12-18概率密度函數 (PDF) 描述了在某個空間區域中觀察到某個連續隨機變量的概率。 對於一維隨機變量 X,回想一下 PDF f(x) 遵循以下屬性:
變量取值之間的概率
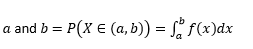
變量取值完全等於的概率
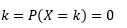
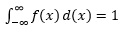
從觀察樣本中估計這樣的 PDF 是機器學習中的常見問題。 這在許多異常值檢測算法中很方便,我們試圖根據樣本觀察估計“真實”分佈,然後將一些現有或新的觀察結果分類為異常值或非異常值。 例如,對發現欺詐感興趣的汽車保險公司可能會檢查每種類型的車身(例如保險槓更換)的索賠金額請求,並將任何過高的金額標記為潛在欺詐。 作為另一個例子,兒童心理學家可以檢查不同兒童完成給定任務所花費的時間,並標記那些花費太長或太短時間進行潛在調查的兒童。
在這篇博客文章中,我們討論瞭如何從觀察樣本中學習 PDF ,以便我們可以計算每個觀察的概率並確定它是常見的還是罕見的。
使用直方圖進行密度估計
首先,我們生成一些隨機數據進行演示。
set.seed(123)
data <- c(rnorm(200, 10, 20), rnorm(200, 60, 30), runif(200, 120, 180)) # 600 points
接下來,我們使用直方圖將它們可視化以供我們理解,如圖 1 所示。
# Plot 1
hist(data, breaks=50, freq=F, main="Univariate Distribution", xlab="Data Value")# Plot 2
hist(data, breaks=20, freq=F, main="", xlab="20 Data Bins", col='red', border='red')
par(new=T)
hist(data, breaks=100, freq=F, main="Univariate Distribution", xlab=NULL, xaxt='n', yaxt='n')
圖 1 – 使用 50-Bin 直方圖的數據可視化
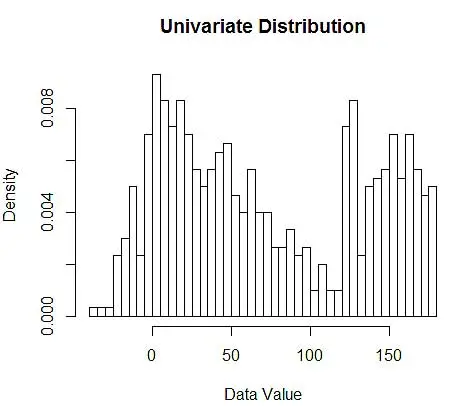
雖然直方圖是數據可視化的圖表,但您也可以看到它們是我們對密度的第一次估計。 更具體地說,我們可以通過將數據劃分為 bin 來估計密度,並假設密度在該 bin 範圍內是恆定的,並且其值等於落入該 bin 的觀察數佔觀察總數的比例
因此,估計的 PDF 為
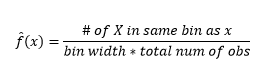
並且您意識到您已經對 bin-width 做出了假設,這將影響密度估計。 因此bin-width 是使用 histogram 的密度估計模型的參數。 然而,被忽略的事實是,我們還使用了另外一個參數——即第一個 bin 的起始位置。 您可以看到這可能如何影響所有箱的密度估計。 為了查看 bin-width 的影響,圖 2 將密度估計與 20-bin 和 100-bin 直方圖重疊。 查看環繞區域,其中較少/較粗的 bin 給出平坦的密度估計,而許多/較細的 bin 給出不同的密度估計。 對於黃點,來自兩個不同模型的密度估計值將在 0.004 到 0.008 之間。
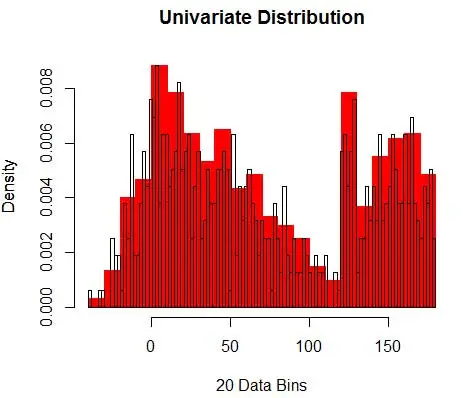
因此,正確選擇參數對於獲得正確的密度估計至關重要。 我們會解決這個問題,但請注意,直方圖還存在其他問題。 使用直方圖的密度估計非常不穩定和不連續。 一個 bin 的密度是平坦的,然後在 bin 外無限小的點突然急劇變化。 這使得錯誤估計的後果對於實際問題更加嚴重。

最後,為了便於說明,我們一直在使用單維變量,但實際上大多數問題都是多維的。 由於箱的數量隨著維度的數量呈指數增長,估計密度所需的觀察數量也會增長。 事實上,儘管有數百萬個觀測值,但許多箱仍然是空的或包含個位數的觀測值,這似乎是合理的。 每個只有 3 個維度的 50 個 bin,我們有 503=125000 個需要填充的單元。 假設均勻分佈,每個單元平均有 8 次觀察,一百萬個觀察訓練數據。
如何選擇合適的參數?
對於 bin 寬度 n 的觀察次數 N 對於 bin J 的觀察比例是
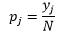
和密度估計是
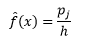
統計理論證明,雖然 f(x) 是 bin 中密度的期望值,但密度的方差是
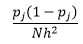
雖然我們可以通過減小 bin-width n 來獲得更好的密度估計,但我們會增加估計的方差,因為我們可以直觀地感覺到 bin-width 太細。 我們可以使用留一法交叉驗證技術來估計最優參數集。 我們可以使用除一個之外的所有觀測值來估計密度,然後計算遺漏觀測值的密度並測量估計誤差。 對直方圖進行數學求解,為給定 bin 寬度的損失函數提供了一個封閉形式的解決方案。
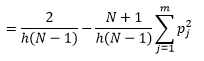
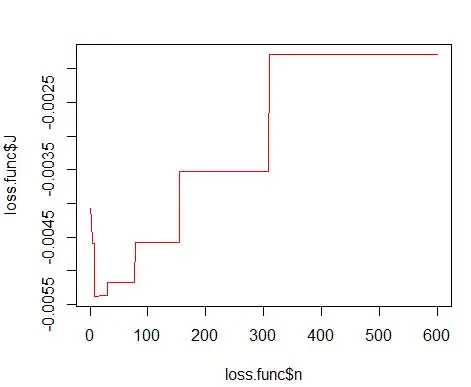
其中 m 是箱數。 上述技術細節在本講座 [pdf] 中。 我們可以針對不同數量的 bin 繪製此損失函數(圖 3)
getLoss <- function(n.break) {
N <- 600
res <- hist(data, breaks=n.break, freq=F)
bin <- as.numeric(res$breaks)
h <- bin[2]-bin[1]
p <- res$density
p <- p * h
return ( 2/(h*(N-1)) - ( (N+1)/(h*(N-1))*sum(p*p) ) )
}loss.func <- data.frame(n=1:600)
loss.func$J <- sapply(loss.func$n, function(x) getLoss(x))
# Plot 3
plot(loss.func$n, loss.func$J, col='red', type='l')
opt.break <- max(loss.func[loss.func$J == min(loss.func$J), 'n'])
print(opt.break)
# Plot 4
hist(data, breaks=opt.break, freq=F, main="Univariate Distribution", xlab="15 Data Bins")
並獲得最佳數字為 15。實際上 8-15 之間的任何值都可以。
因此,圖 4 下面是密度估計,它平衡了密度值和粒度(具有最佳偏差-方差權衡)。
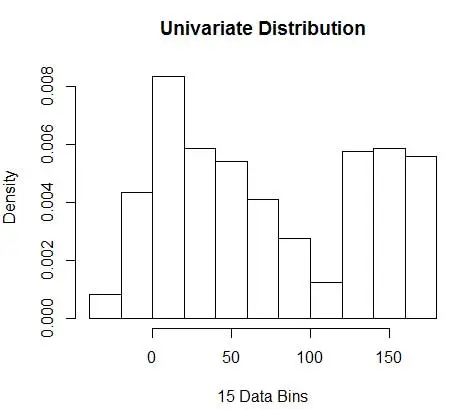
如果你在這一點上感到有點不安,那麼我和你在一起。 儘管 bin 的數量在數學上是最優的,但感覺估計太粗略了。 沒有直觀的感覺為什麼我們做得最好。 並且不要忘記關於起始位置、不連續估計和維度災難的其他問題。 不要失望,有更好的方法。 在下一篇文章中,我們將討論使用內核進行密度估計。
