在超空間測量距離

任何粗略熟悉分析技術的人都會注意到許多算法依賴於數據點之間的距離來進行應用。 每個觀察或數據實例通常表示為多維向量，算法的輸入需要每對這樣的觀察之間的距離。

距離計算方法取決於數據類型——數值、分類或混合。 一些算法只適用於一類觀察，而另一些則適用於多種。 在這篇文章中，我們將討論適用於數值數據的距離度量。 在多維超空間中測量距離的方法可能比單個博客文章中所涵蓋的方法更多，而且人們總是可以發明新的方法，但我們會研究一些常見的距離度量及其相對優點。

出於博客文章其餘部分的目的，我們暗示

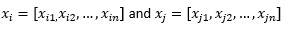
指兩個觀察或數據向量。

首先準備好數據……

在我們查看不同的距離指標之前，我們需要準備數據：

轉換為數值向量

對於同時包含數值維度和分類維度的混合觀察，第一步是將分類維度實際轉換為數值維度。 具有三個潛在值的分類維度可以轉換為具有二進制值的兩個或三個數字維度。 由於該分類變量必須採用三個值之一，因此三個數值維度之一將與其他兩個完全相關。 根據您的應用程序，這可能會也可能不會。

如果觀察是純分類的，例如文本字符串（可變長度的句子）或基因組序列（固定長度的序列），那麼可以直接應用一些特殊的距離度量，而無需將數據轉換為數字格式。 我們將在下一篇文章中討論這些算法。

正常化

根據您的用例，您可能希望以相同的比例對每個維度進行歸一化，以便沿任何一個維度的距離不會過度影響觀測值之間的總距離。 在 k-Means algorithm 中討論了同樣的事情。 有兩種可能的歸一化：

範圍歸一化（重新縮放）通過從每個維度減去最小值然後除以該維度中的值範圍來將數據歸一化為 0-1 範圍。

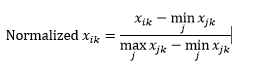
範圍歸一化的第一個問題是看不見的值可能被歸一化到 0-1 範圍之外。 雖然，對於大多數距離度量來說，這通常不是問題，但如果算法不能處理負值，那麼這可能是個問題。 第二個問題是這高度依賴於異常值。 如果一個觀測值對於某個維度具有非常極端的（高或低）值，則其他觀測值的該維度的歸一化值將擠在一起並失去它們的區分能力。

標準歸一化（z 標度）通過從每個觀測值的維度中減去均值，然後除以所有觀測值中該維度值的標準差，將維度歸一化為 0 均值和 1 標準差。

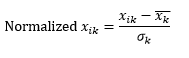
這通常使數據大致保持在-5到+5範圍內，並避免極值的影響。

我們模擬了兩個觀測值的 z 縮放。 模擬，因為我們確實需要兩個以上的觀測值來計算每個維度的均值和標準差，並且我們在這里為每個維度假設了這兩個數字。

然後計算距離...

歐幾里得距離——又名“烏鴉飛”的距離——是多維超空間中兩點之間的最短距離。 您在 2D 平面或 3D 空間（這是一條線）中熟悉這一點，但類似的概念擴展到更高的維度。 n維空間中向量之間的歐幾里得距離計算為

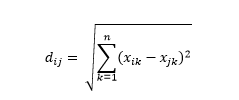
對於轉換後的數據向量示例，這是

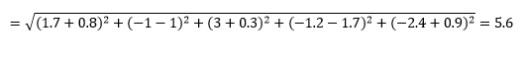
這是最常見的指標，通常非常適合大多數應用程序。 它的一個變體是平方歐幾里得距離，它只是平方差的總和。

曼哈頓距離- 因紐約曼哈頓街道的東西 - 南北 - 南網格結構而得名 - 是平行於軸穿過時兩點之間的距離。

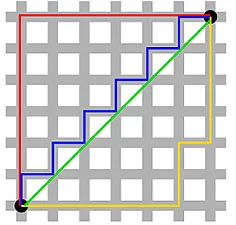
曼哈頓距離
歐幾里得距離

這計算為

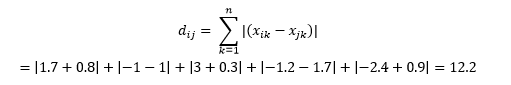
這在某些應用程序中可能很有用，其中距離用於真實的物理意義，而不是機器學習的“差異”意義。 例如，如果您需要計算消防車到達某個點的距離，那麼使用它更實用。

堪培拉距離是曼哈頓距離的加權變體，計算為

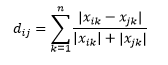
L-範數距離是以上兩個的延伸——或者你可以說以上兩個是 L-範數距離的特定情況——並且被定義為

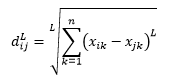
其中 L 是一個正整數。 我沒有遇到任何需要使用它的情況，但這仍然很高興知道可能性。 例如 3 範數距離將是

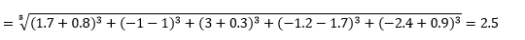
請注意，L 通常應該是偶數，因為我們不希望正或負距離貢獻抵消。

Minkowski 距離是 L 範數距離的推廣，其中 L 可以取從 0 到包括小數值的任何值。 p階的閔可夫斯基距離定義為

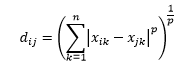
餘弦距離是兩個向量之間角度的度量，每個向量代表兩個觀察值，並通過將數據點連接到原點而形成。 餘弦距離範圍從 0（完全相同）到 1（無連接），計算如下

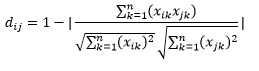
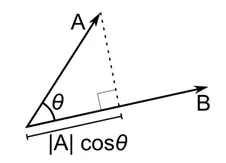
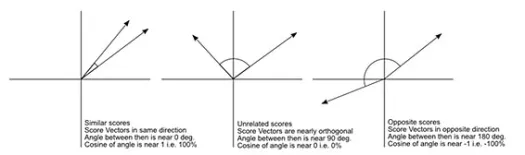
雖然在處理分類數據時這是更常見的距離度量，但也可以為數值向量定義。 對於我們的數值向量，這將是

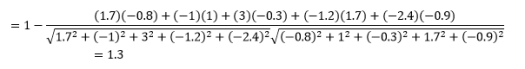
但請注意警告......

你知道這會來的，不是嗎？ 如果分析只是一堆數學公式，我們不需要像你這樣聰明的人來做。

首先要注意的是，不同度量計算的距離是不同的。 您可能會認為 1.3 的餘弦距離是最小的，因此表明向量是最接近的，但這不是正確的解釋方式。 無法比較不同方法之間的距離，只能比較同一方法下不同觀測值對之間的距離。 距離本身有相對意義，沒有絕對意義。

這就引出了下一個問題，即如何選擇正確的距離度量。 不幸的是，沒有真正的答案。 根據數據類型、上下文、業務問題、應用程序和模型訓練方法，不同的指標給出不同的結果。 您將不得不使用判斷、做出假設或測試模型性能來決定正確的指標。

第二個警告是我經常重複的一個關於維度詛咒的問題。 在更高的維度中，距離的行為方式並不像我們直觀地認為的那樣，分析師在使用任何指標時都必須非常謹慎。

第三個警告是關於三個觀察之間的距離之間的關係。 一些指標支持三角不等式，而另一些則不支持。 三角不等式意味著從點 i 直接到點 j 總是最短的，而不是通過任何中間點 k。 數學上，

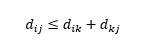
根據您的應用程序，這可能是距離度量的必需屬性，也可能不是。

哦，還有一件事， “距離”與“相似”相反。 距離越高，相似度越低，反之亦然。 聚類算法適用於距離，推薦算法適用於相似性，但本質上它們是在談論同一件事。

那麼，如何將距離數轉換為相似數呢？